
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
1)问题发现
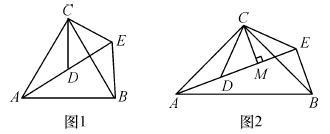
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
科目:czsx 来源:2014-2015学年河北省石家庄市桥西区4月中考模拟数学试卷(解析版) 题型:解答题
问题发现:

如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)求证:△ACD≌△BCE;
(2)求证:CD∥BE.
拓展探究:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,求∠AEB的度数.
科目:czsx 来源:2014-2015学年河北省石家庄市桥西区、裕华区3月中考模拟数学试卷(解析版) 题型:解答题
问题发现:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.

(1)求证:△ACD≌△BCE;
(2)求证:CD∥BE.
拓展探究:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,求∠AEB的度数.
科目:czsx 来源:2014-2015学年江苏省启东市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.

填空:①∠AEB的度数为 ___ ______;
②线段AD,BE之间的数量关系为 ___ ______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D ,E在同一直线上,CM为△DCE中 DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
| 2 |

科目:czsx 来源: 题型:
(1)问题发现
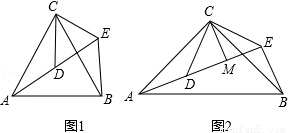
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:
①∠AEB的度数为 ;
②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
(3)解决问题
如图3,在正方形ABCD中,CD=
 ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.


科目:czsx 来源:2015-2016学年重庆市荣昌区八年级上期末数学试卷(解析版) 题型:解答题
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

科目:czsx 来源:2016届河南商丘柘城县张桥中学中考模拟数学试卷(解析版) 题型:解答题
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:
①∠AEB的度数为___________;
②线段AD,BE之间的数量关系为___________.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
(3)解决问题
如图3,在正方形ABCD中,CD= ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.

科目:czsx 来源:2016-2017学年江苏大丰区第一共同体初二上期中考试数学卷(解析版) 题型:解答题
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
科目:czsx 来源: 题型:解答题
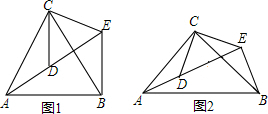
科目:czsx 来源: 题型:解答题
 (1)问题发现
(1)问题发现科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题
 探究题:
探究题:科目:czsx 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)(1)问题发现
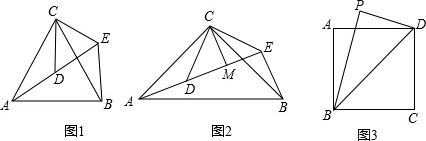
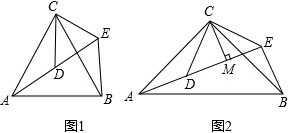
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.

(3)解决问题如图3,在正方形ABCD中,CD= .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

科目:czsx 来源:2015-2016学年江苏省东台市七校八年级上学期期中联考数学试卷(解析版) 题型:解答题
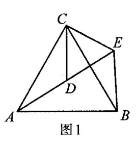
(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
科目:czsx 来源:2015-2016学年四川省泸州市泸县八年级上学期期末数学试卷(解析版) 题型:解答题
(2015•前郭县二模)(1)问题发现
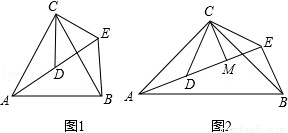
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
