
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2016年初中毕业升学考试(山东泰安卷)数学(解析版) 题型:解答题
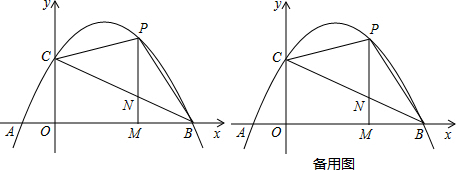
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行与y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
科目:czsx 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.科目:czsx 来源: 题型:
| 1 | 3 |
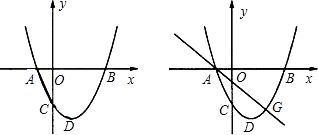 点P运动到什么位置时,点P到直线AG的距离最大?求出此时P点的坐标和点P到直线AG的最大距离.
点P运动到什么位置时,点P到直线AG的距离最大?求出此时P点的坐标和点P到直线AG的最大距离. 科目:czsx 来源: 题型:
 线的顶点,且A,C两点的横坐标分别为1和4.
线的顶点,且A,C两点的横坐标分别为1和4.科目:czsx 来源: 题型:
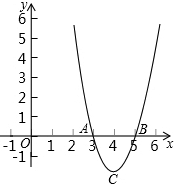 点,顶点为C.
点,顶点为C.科目:czsx 来源: 题型:
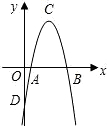
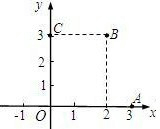 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(3,0)、B(2,3),C(0,3).
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(3,0)、B(2,3),C(0,3).科目:czsx 来源: 题型:
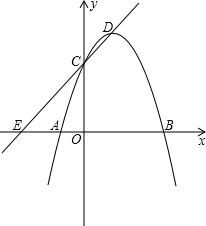 图象顶点为D,OB=OC,tan∠ACO=
图象顶点为D,OB=OC,tan∠ACO=| 1 | 3 |
科目:czsx 来源: 题型:
| ||
| 3 |
 物线上. 动点P在x轴上,以PA为边作等边三角形APQ(△APQ的顶点 A、P、Q按逆时针标记).
物线上. 动点P在x轴上,以PA为边作等边三角形APQ(△APQ的顶点 A、P、Q按逆时针标记).科目:czsx 来源:学习周报 数学 北师大九年级版 2009-2010学年 第18期 总第174期 北师大版 题型:059
如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、C两点的横坐标分别为1和4.
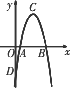
(1)求A、B两点的坐标;
(2)求二次函数的函数表达式;
(3)在(2)的抛物线上,是否存在点P,使得∠BAP=45°?若存在,求出点P的坐标及此时△ABP的面积;若不存在,请说明理由.
科目:czsx 来源:浙江省金华地区2012届九年级下学期3月月考数学试题 题型:044
如图,在平面直角坐标系中,二次函数y=ax2+bx+2的图像与y轴交于点A,对称轴是直线x=![]() ,以OA为边在y轴右侧作等边三角形OAB,点B恰好在该抛物线上.动点P在x轴上,以PA为边作等边三角形APQ(△APQ的顶点A、P、Q按逆时针标记).
,以OA为边在y轴右侧作等边三角形OAB,点B恰好在该抛物线上.动点P在x轴上,以PA为边作等边三角形APQ(△APQ的顶点A、P、Q按逆时针标记).
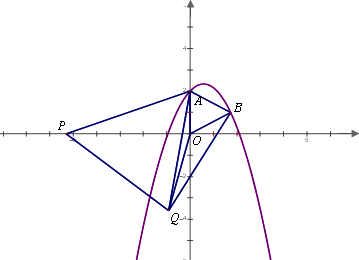
(1)求点B的坐标与抛物线的解析式;
(2)当点P在如图位置时,求证:△APO≌△AQB
(3)当点P在x轴上运动时,点Q刚好在抛物线上,求点Q的坐标.
(4)探究:是否存在点P,使得以A、O、Q、B为顶点的四边形是y梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
科目:czsx 来源:上海市金山区2012届九年级中考二模数学试题 题型:044
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图像经过点A(3,0),B(-1,0),C(0,-3),顶点为D.

(1)求这个二次函数的解析式及顶点坐标;
(2)在y轴上找一点P(点P与点C不重合),使得∠APD=90°,求点P坐标;
(3)在(2)的条件下,将△APD沿直线AD翻折,得到△AQD,求点Q坐标.
科目:czsx 来源:2008年广东省深圳市初中毕业升学统一考试、数学试卷 题型:059
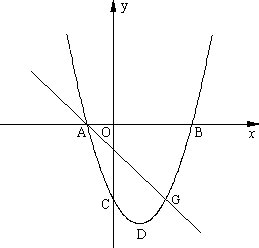
如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,tan∠ACO=![]() .
.

(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
(4)如图,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
科目:czsx 来源: 题型:解答题
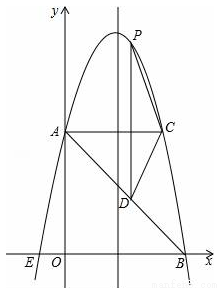
 有两条抛物线l1、l2都经过A、B两点,且关于AB所在直线对称,其中抛物线l1经过原点,抛物线l2交y轴于点E.设P、Q两点分别在抛物线l1、l2上运动.
有两条抛物线l1、l2都经过A、B两点,且关于AB所在直线对称,其中抛物线l1经过原点,抛物线l2交y轴于点E.设P、Q两点分别在抛物线l1、l2上运动. ,直接写出b的取值范围.
,直接写出b的取值范围. ,
, )】
)】科目:czsx 来源: 题型:解答题
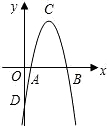 线的顶点,且A,C两点的横坐标分别为1和4.
线的顶点,且A,C两点的横坐标分别为1和4.科目:czsx 来源: 题型:解答题
 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(3,0)、B(2,3),C(0,3).
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(3,0)、B(2,3),C(0,3).科目:czsx 来源: 题型:解答题
 图象顶点为D,OB=OC,tan∠ACO=
图象顶点为D,OB=OC,tan∠ACO= .
.科目:czsx 来源: 题型:解答题
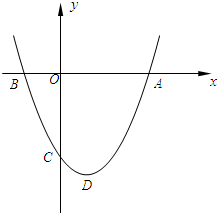 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(3,0),B(-1,0),C(0,-3),顶点为D.
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(3,0),B(-1,0),C(0,-3),顶点为D.科目:czsx 来源: 题型:解答题
 ,0),以0C为直径作半圆,圆心为D.
,0),以0C为直径作半圆,圆心为D.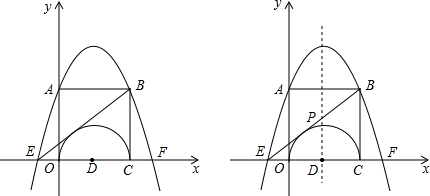
科目:czsx 来源: 题型:解答题
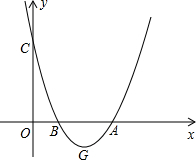 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过A(3,0)、B(1,0)、C(0.3)三点,设该二次函数的顶点为G.
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过A(3,0)、B(1,0)、C(0.3)三点,设该二次函数的顶点为G.