
科目:czsx 来源: 题型:
 如图,在Rt△ABC中,AB=BC,D为AC边的中点,过点D作DE⊥DF,交AB于点E,交BC于点F.
如图,在Rt△ABC中,AB=BC,D为AC边的中点,过点D作DE⊥DF,交AB于点E,交BC于点F.科目:czsx 来源:不详 题型:解答题

科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
 如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别为AB、BC的中点,AE与CD相交于点H,CF⊥AE交AB于点F,垂足为G,连结EF、FH和DG.
如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别为AB、BC的中点,AE与CD相交于点H,CF⊥AE交AB于点F,垂足为G,连结EF、FH和DG.科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
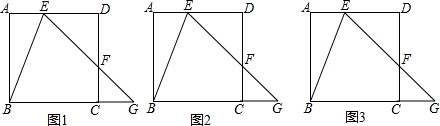
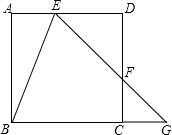 如图,正方形ABCD中,E、F分别在AD、DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
如图,正方形ABCD中,E、F分别在AD、DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;| 1 |
| 2 |
科目:czsx 来源:2014-2015学年重庆市九年级下学期期中考试数学试卷(解析版) 题型:解答题
如图1, ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.
ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.
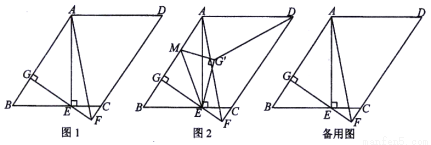
(1)若BE=2EC,AB = ,求AD的长;
,求AD的长;
(2)求证:EG=BG+FC;
(3)如图2,若AF= ,EF=2,点
,EF=2,点 是线段 AG上的一个动点,连接
是线段 AG上的一个动点,连接 ,将
,将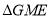 沿
沿 翻折得
翻折得
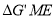 ,连接
,连接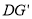 ,试求当
,试求当 取得最小值时
取得最小值时 的长.
的长.
科目:czsx 来源:2014-2015学年山东省烟台市龙口市八年级下学期期末数学试卷(解析版) 题型:解答题
如图1,正方形ABCD中,E、F分别在AD、DG上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;

(1)求证:∠ABE= ∠BGE;
∠BGE;
(2)如图2,若AB=5,AE=2,求S△BEG;
(3)如图3,若E、F两点分别在AD、DC上运动,其它条件不变,试问:线段AE、EF、FC三者之间是否存在确定的数量关系?若存在,请写出它们之间的数量关系,并证明;若不存在,请说明理由.
科目:czsx 来源:2015-2016学年广西省钦州市钦南区八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别为AB、BC的中点,AE与CD相交于点H,CF⊥AE交AB于点F,垂足为G,连结EF、FH和DG.

(1)求证:△ACH≌△CBF;
(2)求证:AE=EF+FC;
(3)若AC=6,求线段DG的长.
科目:czsx 来源: 题型:
 如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F.
如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F.科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
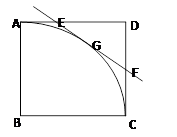
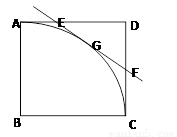
如图,在正方形ABCD中,AB=1,AC是以点B为圆心,AB长为半径的圆的一条弧,点E是边AD上的任意一点(点E与A、D不重合),过E作AC所在圆的切线,交边DC于点F,G为切点
1.当∠DEF=![]() 时,试说明点G为线段EF的中点;
时,试说明点G为线段EF的中点;
2.设AE=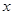 ,FC=
,FC= ,用含有
,用含有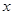 的代数式来表示
的代数式来表示 ,并写出
,并写出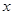 的取值范围
的取值范围
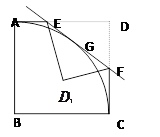
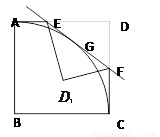
3.如果把△DEF沿直线EF对折后得△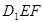 ,如图2,当
,如图2,当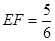 时,讨论△
时,讨论△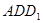 与△
与△![]() 是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
科目:czsx 来源:2011-2012学年江苏扬州中学教育集团九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,在正方形ABCD中,AB=1,AC是以点B为圆心,AB长为半径的圆的一条弧,点E是边AD上的任意一点(点E与A、D不重合),过E作AC所在圆的切线,交边DC于点F,G为切点
1.当∠DEF= 时,试说明点G为线段EF的中点;
时,试说明点G为线段EF的中点;
2.设AE= ,FC=
,FC=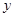 ,用含有
,用含有 的代数式来表示
的代数式来表示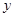 ,并写出
,并写出 的取值范围
的取值范围
3.如果把△DEF沿直线EF对折后得△ ,如图2,当
,如图2,当 时,讨论△
时,讨论△ 与△
与△ 是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
科目:czsx 来源: 题型:
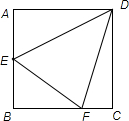 如图,在正方形ABCD中,AB=6,用一块含45°的三角板,把45°角的顶点放在D点,将三角板绕着点D旋转,使这个45°角的两边与线段AB、BC分别相交于点E、F.
如图,在正方形ABCD中,AB=6,用一块含45°的三角板,把45°角的顶点放在D点,将三角板绕着点D旋转,使这个45°角的两边与线段AB、BC分别相交于点E、F.科目:czsx 来源:2003年上海市中考数学试题 题型:059
| |||||||||||||||
科目:czsx 来源: 题型:解答题
 如图,在正方形ABCD中,AB=6,用一块含45°的三角板,把45°角的顶点放在D点,将三角板绕着点D旋转,使这个45°角的两边与线段AB、BC分别相交于点E、F.
如图,在正方形ABCD中,AB=6,用一块含45°的三角板,把45°角的顶点放在D点,将三角板绕着点D旋转,使这个45°角的两边与线段AB、BC分别相交于点E、F.科目:czsx 来源:不详 题型:解答题
 时,试说明点G为线段EF的中点;
时,试说明点G为线段EF的中点; ,FC=
,FC= ,用含有
,用含有 的代数式来表示
的代数式来表示 ,并写出
,并写出 的取值范围
的取值范围 ,如图2,当
,如图2,当 时,讨论△
时,讨论△ 与△
与△ 是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
