
科目:gzsx 来源:2013届福建省泉州市高二下学期期中文科数学试卷(解析版) 题型:解答题
已知 ,设
,设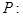
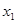 和
和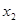 是方程
是方程 的两个根,不等式
的两个根,不等式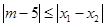 对任意实数
对任意实数 恒成立;
恒成立;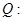 函数
函数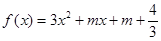 有两个不同的零点.求使“P且Q”为真命题的实数
有两个不同的零点.求使“P且Q”为真命题的实数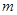 的取值范围.
的取值范围.
【解析】本试题主要考查了命题和函数零点的运用。由题设x1+x2=a,x1x2=-2,
∴|x1-x2|=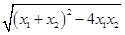 =
=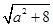 .
.
当a∈[1,2]时,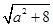 的最小值为3. 当a∈[1,2]时,
的最小值为3. 当a∈[1,2]时,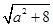 的最小值为3.
的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判别式
=0的判别式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
可得到要使“P∧Q”为真命题,只需P真Q真即可。
解:由题设x1+x2=a,x1x2=-2,
∴|x1-x2|=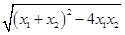 =
=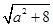 .
.
当a∈[1,2]时,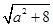 的最小值为3.
的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判别式
=0的判别式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
综上,要使“P∧Q”为真命题,只需P真Q真,即
解得实数m的取值范围是(4,8]
科目:gzsx 来源:2014-2015学年江西省高二上学期开学考试数学试卷(解析版) 题型:解答题
已知函数 (
( R,且
R,且 )的部分图象如图所示.
)的部分图象如图所示.

(1) 求 的值;
的值;
(2) 若方程 在
在 内有两个不同的解,求实数m的取值范围.
内有两个不同的解,求实数m的取值范围.
科目:gzsx 来源: 题型:
科目:gzsx 来源:不详 题型:解答题
科目:gzsx 来源:2011-2012学年江苏省苏州市高三(上)期末数学试卷(解析版) 题型:解答题
科目:gzsx 来源:2012年江苏省苏州市高三1月调研数学试卷(解析版) 题型:解答题
科目:gzsx 来源: 题型:解答题
科目:gzsx 来源: 题型:解答题
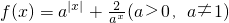 ,
,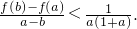
科目:gzsx 来源:2010年江苏省连云港市东海高级中学高考数学考前猜题试卷(2)(解析版) 题型:解答题
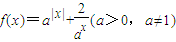 ,
,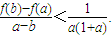
科目:gzsx 来源: 题型:解答题
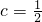 时,求出不等式f(x)<0的解;
时,求出不等式f(x)<0的解;科目:gzsx 来源:闵行区一模 题型:解答题
| 1 |
| 2 |
科目:gzsx 来源:2008年上海市闵行区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
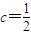 时,求出不等式f(x)<0的解;
时,求出不等式f(x)<0的解;科目:gzsx 来源: 题型:
| 1 |
| 2 |
科目:gzsx 来源:2013-2014学年江苏南京金陵中学高三第一学期期中考试理科数学试卷(解析版) 题型:解答题
已知函数f(x)=a|x|+ (a>0,a≠1)
(a>0,a≠1)
(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)= f( x),x∈[ 2,+∞), 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
科目:gzsx 来源: 题型:解答题
已知函数f(x)=a|x|+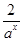 (a>0,a≠1)
(a>0,a≠1)
(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)=" f(" x),x∈[ 2,+∞),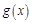 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.