
科目:gzsx 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
在平面直角坐标系中O为坐标原点,P(3,4),将向量 绕原点顺时针方向旋转
绕原点顺时针方向旋转 ,并将其长度伸长为原来的2倍的向量
,并将其长度伸长为原来的2倍的向量 ,则点Q的坐标是( )
,则点Q的坐标是( )
A.(3+4 ,4﹣3
,4﹣3 ) B.(4+3
) B.(4+3 ,4﹣3
,4﹣3 )
)
C.(3+4 ,3
,3 ) D.(3﹣4
) D.(3﹣4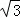 ,3﹣4
,3﹣4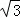 )
)
科目:gzsx 来源:不详 题型:单选题
| OP |
| π |
| 3 |
| OQ |
A.(3+4
| B.(4+3
| C.(3+4
| D.(3-4
|
科目:gzsx 来源:2012-2013学年山东省德州市高三(上)校际联考数学试卷(文科)(解析版) 题型:选择题
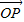 绕原点顺时针方向旋转
绕原点顺时针方向旋转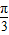 ,并将其长度伸长为原来的2倍的向量
,并将其长度伸长为原来的2倍的向量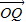 ,则点Q的坐标是( )
,则点Q的坐标是( )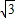 ,4-3
,4-3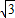 )
)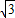 ,4-3
,4-3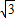 )
)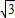 ,3
,3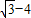 )
)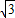 ,3-4
,3-4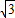 )
)科目:gzsx 来源:2012-2013学年山东省德州市高三(上)校际联考数学试卷(理科)(解析版) 题型:选择题
 绕原点顺时针方向旋转
绕原点顺时针方向旋转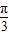 ,并将其长度伸长为原来的2倍的向量
,并将其长度伸长为原来的2倍的向量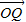 ,则点Q的坐标是( )
,则点Q的坐标是( )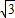 ,4-3
,4-3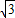 )
)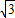 ,4-3
,4-3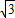 )
) ,3
,3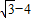 )
)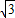 ,3-4
,3-4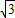 )
)科目:gzsx 来源: 题型:

(1)求动点P的轨迹C的方程;
(2)点Q是直线y=-1上的一个动点,过点Q作轨迹C的两条切线,切点分别为M、N,求证:QM⊥QN.
科目:gzsx 来源:2010-2011学年湖南省长沙市长望浏宁四县高三3月调研考试数学理卷 题型:填空题
在平面直角坐标系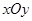 中,
中,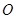 为坐标原点.定义
为坐标原点.定义 、
、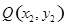 两点之间的“直角距离”为
两点之间的“直角距离”为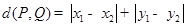 .若点
.若点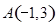 ,则
,则 =
;已知点
=
;已知点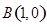 ,点M是直线
,点M是直线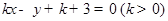 上的动点,
上的动点,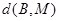 的最小值为 .
的最小值为 .
14.如图,半径为2的⊙O中,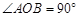 ,
,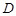 为
为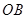 的中点,
的中点,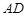 的延长线交⊙O于点
的延长线交⊙O于点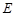 ,则线段
,则线段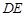 的长为
的长为
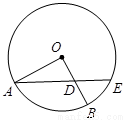
科目:gzsx 来源:2011届湖南省长沙市长望浏宁四县高三3月调研考试数学理卷 题型:填空题
在平面直角坐标系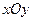 中,
中, 为坐标原点.定义
为坐标原点.定义 、
、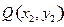 两点之间的“直角距离”为
两点之间的“直角距离”为 .若点
.若点 ,则
,则 = ;已知点
= ;已知点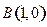 ,点M是直线
,点M是直线 上的动点,
上的动点, 的最小值为 .
的最小值为 .
14.如图,半径为2的⊙O中, ,
,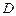 为
为 的中点,
的中点,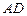 的延长线交⊙O于点
的延长线交⊙O于点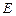 ,则线段
,则线段 的长为
的长为 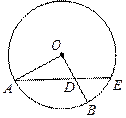
科目:gzsx 来源:不详 题型:填空题
 中,
中, 为坐标原点.定义
为坐标原点.定义 、
、 两点之间的“直角距离”为
两点之间的“直角距离”为 .若点
.若点 ,则
,则 = ;已知点
= ;已知点 ,点M是直线
,点M是直线 上的动点,
上的动点, 的最小值为 .
的最小值为 . ,
, 为
为 的中点,
的中点, 的延长线交⊙O于点
的延长线交⊙O于点 ,则线段
,则线段 的长为
的长为 
科目:gzsx 来源: 题型:
2
| ||
| 3 |
| π |
| 2 |
|
科目:gzsx 来源: 题型:
2
| ||
| 3 |
| π |
| 2 |
|
科目:gzsx 来源: 题型:
| 2 |
| π |
| 4 |
|
科目:gzsx 来源: 题型:
|
科目:gzsx 来源:2012年全国普通高等学校招生统一考试理科数学(福建卷解析版) 题型:解答题
在平面直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系。已知直线l上两点M,N的极坐标分别为(2,0)
【解析】


科目:gzsx 来源:2012-2013学年福建省泉州市德化三中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
 ,曲线C的参数方程
,曲线C的参数方程 (θ为参数且0<θ<π).
(θ为参数且0<θ<π).科目:gzsx 来源: 题型:填空题
科目:gzsx 来源: 题型:解答题
科目:gzsx 来源:高考真题 题型:解答题
 ),圆C的参数方程
),圆C的参数方程 (θ为参数)。
(θ为参数)。