
科目:czsx 来源:2014年初中毕业升学考试(黑龙江哈尔滨卷)数学(解析版) 题型:解答题
如图,在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,∠ADB=∠CAD+∠ABD,∠BAD=3∠CBD.
(1)求证:△ABC为等腰三角形;
(2)M是线段BD上一点,BM:AB=3:4,点F在BA的延长线上,连接FM,∠BFM的平分线FN交BD于点N,交AD于点G,点H为BF中点,连接MH,当GN=GD时,探究线段CD、FM、MH之间的数量关系,并证明你的结论.

科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
如图,在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,∠ADB=∠CAD+∠ABD,∠BAD=3∠CBD.
(1)求证:△ABC为等腰三角形;
(2)M是线段BD上一点,BM:AB=3:4,点F在BA的延长线上,连接FM,∠BFM的平分线FN交BD于点N,交AD于点G,点H为BF中点,连接MH,当GN=GD时,探究线段CD、FM、MH之间的数量关系,并证明你的结论.

科目:czsx 来源: 题型:
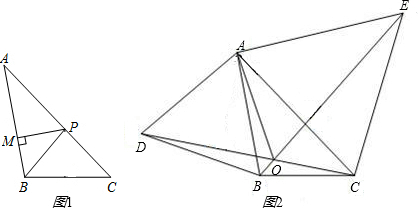
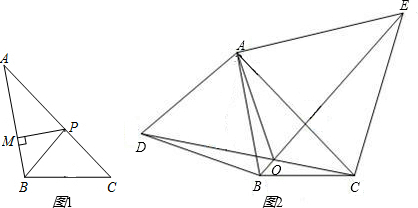
科目:czsx 来源:2011—2012学年北京市首师大附中八年级上学期期中考试数学试卷(带解析) 题型:解答题
(1)如图1,BP为 ABC的角平分线,PM
ABC的角平分线,PM AB于M,PN
AB于M,PN BC于N,AB =30,BC =23,求
BC于N,AB =30,BC =23,求 ABP与
ABP与 BPC的面积的比值;
BPC的面积的比值;
(2)如图2,分别以 ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断
ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断 AOD与
AOD与 AOE的数量关系,并证明;
AOE的数量关系,并证明;
(3)在四边形ABCD中,已知BC=DC,且AB≠AD,对角线AC平分 BAD,请画出图形,并直接写出
BAD,请画出图形,并直接写出 B和
B和 D的数量关系.
D的数量关系.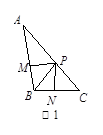

科目:czsx 来源:2013届北京市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(1)如图1,BP为 ABC的角平分线,PM
ABC的角平分线,PM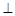 AB于M,PN
AB于M,PN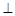 BC于N,AB =30,BC =23,求
BC于N,AB =30,BC =23,求 ABP与
ABP与 BPC的面积的比值;
BPC的面积的比值;
(2)如图2,分别以 ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断
ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断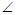 AOD与
AOD与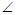 AOE的数量关系,并证明;
AOE的数量关系,并证明;
(3)在四边形ABCD中,已知BC=DC,且AB≠AD,对角线AC平分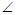 BAD,请画出图形,并直接写出
BAD,请画出图形,并直接写出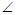 B和
B和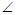 D的数量关系.
D的数量关系.


科目:czsx 来源: 题型:解答题
科目:czsx 来源:2010年北京市昌平区中考数学二模试卷(解析版) 题型:解答题

科目:czsx 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:解答题
阅读下面材料:
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.
小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.

科目:czsx 来源:不详 题型:解答题

科目:czsx 来源: 题型:

科目:czsx 来源:2014-2015学年河南省九年级下学期综合练习一考试数学试卷(解析版) 题型:解答题
阅读下面材料:
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.

小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.
