
科目:czsx 来源:数学教研室 题型:044
在等腰△ABC中,B、C为定点,且AC=AB,D为BC的中点,以BC为直径作⊙D.
(1)顶角A等于多少度时,点A在⊙D上?
(2)顶角A等于多少度时,点A在⊙D内部?
(3)顶角A等于多少度时,点A在⊙D外部?
科目:czsx 来源: 题型:044
在等腰△ABC中,B、C为定点,且AC=AB,D为BC的中点,以BC为直径作⊙D.
(1)顶角A等于多少度时,点A在⊙D上?
(2)顶角A等于多少度时,点A在⊙D内部?
(3)顶角A等于多少度时,点A在⊙D外部?
科目:czsx 来源: 题型:解答题
在等腰△ABC中,B、C为定点,且AC=AB,D为BC的中点,以BC为直径作⊙D,问:
(1)顶角A等于多少度时,点A在⊙D上?(2)顶角A等于多少度时,点A在⊙D内部?(3)顶角A等于多少度时,点A在⊙D外部?
科目:czsx 来源:《24.2.1 点和圆的位置关系》2009年同步练习(解析版) 题型:解答题
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:解答题
科目:czsx 来源:不详 题型:解答题

 BAE = y,求y关于x的函数解析式,并写出它的定义域;
BAE = y,求y关于x的函数解析式,并写出它的定义域;科目:czsx 来源: 题型:
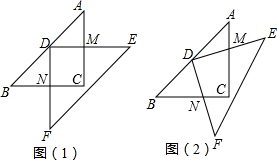
 已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.
已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.科目:czsx 来源: 题型:单选题
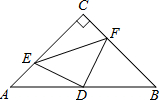 如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论: .其中正确的结论是
.其中正确的结论是科目:czsx 来源:拱墅区一模 题型:单选题
| 2 |
| A.①④ | B.②③ | C.①②④ | D.①②③④ |

科目:czsx 来源:2013年浙江省杭州市拱墅区中考数学一模试卷(解析版) 题型:选择题
 .其中正确的结论是( )
.其中正确的结论是( )
科目:czsx 来源:2014-2015学年河北省保定市博野县中考一模数学试卷(解析版) 题型:选择题
如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①四边形CEDF有可能成为正方形;
②△DFE是等腰直角三角形;
③四边形CEDF的面积是定值;
④点C到线段EF的最大距离为 .
.
其中正确的结论是( )

A.①④ B.②③ C.①②④ D.①②③④
科目:czsx 来源:2016届江西省景德镇市中考二模数学试卷(解析版) 题型:解答题
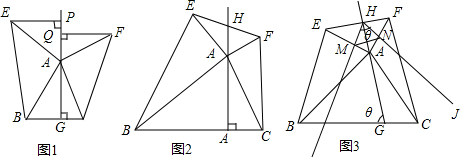
【特例发现】如图1,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.求证:EP=FQ.
【延伸拓展】如图2,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作Rt△ABE和Rt△ACF,射线GA交EF于点H.若AB=kAE,AC=kAF,请思考HE与HF之间的数量关系,并直接写出你的结论.
【深入探究】如图3,在△ABC中,G是BC边上任意一点,以A为顶点,向△ABC外作任意△ABE和△ACF,射线GA交EF于点H.若∠EAB=∠AGB,∠FAC=∠AGC,AB=kAE,AC=kAF,上一问的结论还成立吗?并证明你的结论.
【应用推广】在上一问的条件下,设大小恒定的角∠IHJ分别与△AEF的两边AE、AF分别交于点M、N,若△ABC为腰长等于4的等腰三角形,其中∠BAC=120°,且∠IHJ=∠AGB=θ=60°,k=2;
求证:当∠IHJ在旋转过程中,△EMH、△HMN和△FNH均相似,并直接写出线段MN的最小值(请在答题卡的备用图中补全作图).

科目:czsx 来源: 题型:填空题
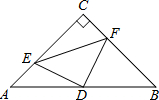 如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
 (2013•拱墅区一模)如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
(2013•拱墅区一模)如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:| 2 |
科目:czsx 来源:2015届浙江宁波宁海长街镇初中初二上第三次月考数学卷(解析版) 题型:选择题
等腰三角形ABC中,AB=AC=5,BC=6,建立适当的直角坐标系,使B、C两点落在 轴上,且关于
轴上,且关于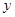 轴对称时,A点坐标为(
)
轴对称时,A点坐标为(
)
A.(0,4) B.(0,-4) C.(0,4)或(0,-4) D.无法确定
科目:czsx 来源:不详 题型:单选题
 轴上,且关于
轴上,且关于 轴对称时,A点坐标为( )
轴对称时,A点坐标为( )科目:czsx 来源: 题型:
等腰三角形ABC中,AB=AC=5,BC=6,建立适当的直角坐标系,使B、C两点落在![]() 轴上,且关
轴上,且关![]() 于
于![]() 轴对称时,A点坐标为( )
轴对称时,A点坐标为( )
A.(0,4) B.(0,-4) C.(0,4)或(0,-4) D.无法确定