科目:czsx 来源: 题型:单选题
如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )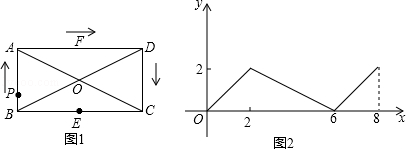
| A.点C&nbs, | B.点O&nbs, | C.点E&nbs, | D.点F&nbs, |
科目:czsx 来源:2015届北京市顺义区八年级下学期期末考试数学试卷(解析版) 题型:选择题
如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )

A.点C B.点O C.点E D.点F
科目:czsx 来源: 题型:

| A、点C | B、点O | C、点E | D、点F |
科目:czsx 来源:2014-2015学年北京市延庆县九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )

A.点C B.点F C.点D D.点O
科目:czsx 来源: 题型:解答题
 如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动,过点Q作QM∥AC交AD于点M,连接PM,PQ,设点P的运动时间为t秒,△PQM的面积为S.
如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动,过点Q作QM∥AC交AD于点M,连接PM,PQ,设点P的运动时间为t秒,△PQM的面积为S.科目:czsx 来源: 题型:解答题
 如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动.过点Q作QM∥AC交AD于点M,连接PM,PQ.设点P的运动时间为t秒,△PQM的面积为s.
如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动.过点Q作QM∥AC交AD于点M,连接PM,PQ.设点P的运动时间为t秒,△PQM的面积为s.科目:czsx 来源: 题型:单选题
如图,在矩形ABCD中,AB=2cm,BC=4cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度分别沿B→C,C→D运动,点F运动到点D时停止,点E运动到点C时停止.设运动时间为t(单位:s),△OEF的面积为S(单位:cm2),则S与t的函数关系可用图象表示为( )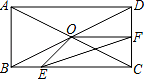

科目:czsx 来源:2015届北京市昌平区八年级下学期期末考试数学试卷(解析版) 题型:选择题
如图,在矩形ABCD中,AB=2cm,BC=4cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度分别沿B→C,C→D运动,点F运动到点D时停止,点E运动到点C时停止.设运动时间为t(单位:s),△OEF的面积为S(单位:cm2),则S与t的函数关系可用图象表示为( )


科目:czsx 来源: 题型:
 如图,在矩形ABCD中,AB=2cm,BC=4cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度分别沿B→C,C→D运动,点F运动到点D时停止,点E运动到点C时停止.设运动时间为t(单位:s),△OEF的面积为S(单位:cm2),则S与t的函数关系可用图象表示为( )
如图,在矩形ABCD中,AB=2cm,BC=4cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度分别沿B→C,C→D运动,点F运动到点D时停止,点E运动到点C时停止.设运动时间为t(单位:s),△OEF的面积为S(单位:cm2),则S与t的函数关系可用图象表示为( )A、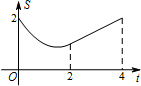 |
B、 |
C、 |
D、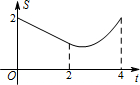 |
科目:czsx 来源: 题型:
 如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).科目:czsx 来源: 题型:
如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)求点N落在BD上时t的值;
(2)直接写出点O在正方形PQMN内部时t的取值范围;
(3)当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;
(4)直接写出直线DN平分△BCD面积时t的值.

科目:czsx 来源: 题型:
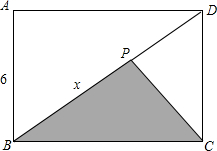 如图,在矩形ABCD中,AB=6,BC=8,动点P从B出发,沿对角线BD向点D运动,连接PC,设BP=x,相应的△PBC的面积为S,试求S与x之间的函数关系式.
如图,在矩形ABCD中,AB=6,BC=8,动点P从B出发,沿对角线BD向点D运动,连接PC,设BP=x,相应的△PBC的面积为S,试求S与x之间的函数关系式.科目:czsx 来源: 题型:
如图1,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
A.点C B.点O C.点E D.点F
科目:czsx 来源: 题型:
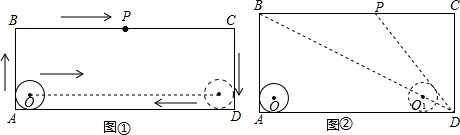
如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4),半径为2cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置)
(1)如图①,点P从A→B→C→D,全程共移动了 cm(用含a、b的代数式表示);
(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离;
 (3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由.
(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由.
科目:czsx 来源:2016届江苏省江阴市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4),半径为2cm的⊙O在矩形内且与AB、AD均相切,现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动.⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动,已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).
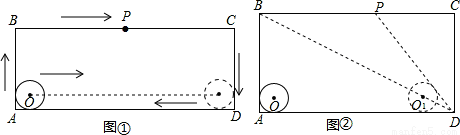
(1)如图①,点P从A→B→C→D,全程共移动了 cm(用含a、b的代数式表示);
(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点,若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离;
(3)如图②,已知a=20,b=10,是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由.
科目:czsx 来源:2016届江苏省江阴市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4),半径为2cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).
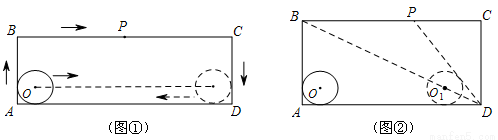
(1)如图①,点P从A→B→C→D,全程共移动了 cm(用含a、b的代数式表示);
(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离;
(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由.
科目:czsx 来源:2016年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:解答题
如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t< ).
).

(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
科目:czsx 来源:2017届江苏无锡江阴市长泾片九年级上期中数学试卷(解析版) 题型:解答题
如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<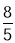 ).
).
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.

科目:czsx 来源:2017届江苏无锡惠山区九年级上期末数学试卷(解析版) 题型:解答题
如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t< ).
).

(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)在运动过程中,当直线MN与⊙O相切时,求t的值.
科目:czsx 来源: 题型:解答题