
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
操作与探究
列代数式:比 的2倍少4的数记作A,则A=________________
的2倍少4的数记作A,则A=________________
 比
比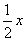 的相反数多2的数记作B,则B=______________.
的相反数多2的数记作B,则B=______________.
(1) 根据所给 的值求上述代数式的值并填入表格:
的值求上述代数式的值并填入表格:
|
| … | 0 | 1 | 2 | 3 | 4 | … |
| A | … | … | |||||
| B | … | … |
(2) 观察归纳:代数式A的值随 的增大而__________
的增大而__________
代数式B的值随 的增大而__________
的增大而__________
(填“增大”或“减小”)
当A>B时,整数 的最小值是________.
的最小值是________.
(3) 若A和B的值相差3,求
 的值.
的值.
科目:czsx 来源: 题型:解答题
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用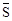 表示,例如图1中,
表示,例如图1中,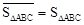 ,图2中,
,图2中,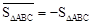 .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组(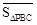 ,
,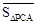 ,
,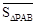 )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作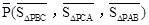 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2,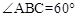 ,则
,则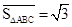 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标”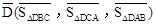 为
为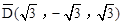 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: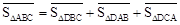 .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则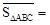 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系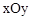 中,点
中,点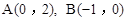 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于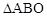 的“面积坐标”为
的“面积坐标”为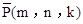 ,
,
试探究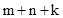 与
与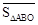 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点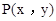 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于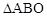 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点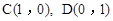 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.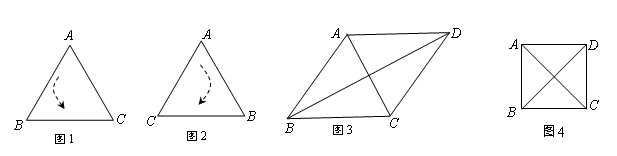
科目:czsx 来源:不详 题型:解答题
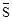 表示,例如图1中,
表示,例如图1中,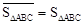 ,图2中,
,图2中,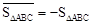 .
.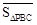 ,
,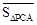 ,
,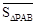 )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作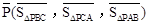 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2,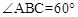 ,则
,则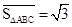 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标”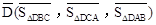 为
为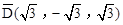 .在图3中,我们知道
.在图3中,我们知道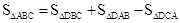 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: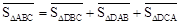 .
.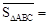 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现: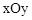 中,点
中,点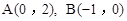 ,
,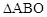 的“面积坐标”为
的“面积坐标”为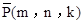 ,
,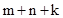 与
与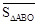 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;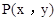 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于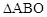 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);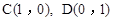 ,点Q在抛物线
,点Q在抛物线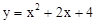 上,求当
上,求当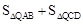 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.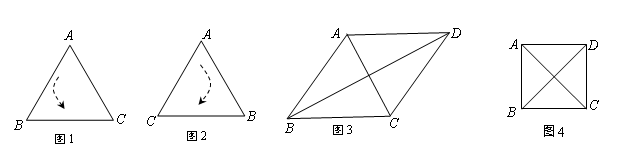
科目:czsx 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用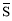 表示,例如图1中,
表示,例如图1中,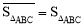 ,图2中,
,图2中, .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组( ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: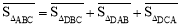 .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系 中,点
中,点 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.

科目:czsx 来源: 题型:
. |
| S |
. |
| S △ABC |
. |
| S △ABC |
. |
| S △PBC |
. |
| S △PCA |
. |
| S △PAB |
. |
| P |
. |
| S △PBC |
. |
| S △PCA |
. |
| S △PAB |
. |
| S △ABC |
| 3 |
. |
| D |
. |
| S △DBC |
. |
| S △DCA |
. |
| S △DAB |
. |
| D |
| 3 |
| 3 |
| 3 |
. |
| S △ABC |
. |
| S △DBC |
. |
| S △DAB |
. |
| S △DCA |
. |
| S △ABC |
. |
| P |
. |
| S △ABO |

科目:czsx 来源: 题型:解答题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| A | … | … | |||||
| B | … | … |
科目:czsx 来源: 题型:
| a+b | m |
科目:czsx 来源: 题型:
| 2a+2b |
| m+2 |
| 1 |
| 2 |