
科目:gzsx 来源:2011-2012学年甘肃省高三百题集理科数学试卷(解析版)(四) 题型:解答题
设点F(0,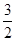 ),动圆P经过点F且和直线y=
),动圆P经过点F且和直线y=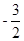 相切,记动圆的圆心P的轨迹为曲线W.
相切,记动圆的圆心P的轨迹为曲线W.
⑴求曲线W的方程;⑵过点F作相互垂直的直线 ,
, ,分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值;②分别在A,B两点作曲线W的切线,这两条切线的交点记为Q,求证:QA⊥QB,且点Q在某一定直线上。
,分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值;②分别在A,B两点作曲线W的切线,这两条切线的交点记为Q,求证:QA⊥QB,且点Q在某一定直线上。
科目:gzsx 来源:不详 题型:解答题
 ),动圆P经过点F且和直线y=
),动圆P经过点F且和直线y= 相切,记动圆的圆心P的轨迹为曲线W.
相切,记动圆的圆心P的轨迹为曲线W. ,
, ,分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值;②分别在A,B两点作曲线W的切线,这两条切线的交点记为Q,求证:QA⊥QB,且点Q在某一定直线上。
,分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值;②分别在A,B两点作曲线W的切线,这两条切线的交点记为Q,求证:QA⊥QB,且点Q在某一定直线上。科目:gzsx 来源: 题型:解答题
科目:gzsx 来源: 题型:解答题
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| |AC|2|BD|2 |
| |AC|+|BD| |
科目:gzsx 来源:新疆乌鲁木齐一中2012届高三上学期第三次月考数学理科试题 题型:044
已知![]() ,B、D是圆上两动点,且四边形ABCD是矩形
,B、D是圆上两动点,且四边形ABCD是矩形
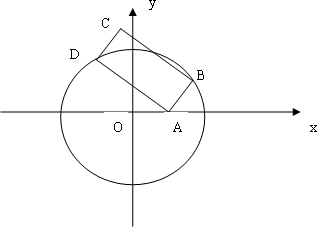
(1)求顶点C的轨迹E的方程;
(2)若过点F(2,0)作曲线E的互相垂直的弦PQ和MN,求四边形PMQN面积的最大值和此时弦所在的直线方程.
科目:gzsx 来源: 题型:
设点![]() 动圆P经过点F且和直线
动圆P经过点F且和直线![]() 相切,记动圆的圆心P的轨迹为曲线W。
相切,记动圆的圆心P的轨迹为曲线W。
(1)求曲线W的方程;
(2)过点F作互相垂直的直线![]() ,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
(3)分别在A、B两点作曲线W的切线,这两条切线的交点记为Q。
求证:QA⊥QB,且点Q在某一定直线上。
科目:gzsx 来源:甘肃省兰州五十五中2011-2012学年高三第一次月考试题(数学理) 题型:解答题
设点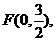 动圆P经过点F且和直线
动圆P经过点F且和直线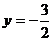 相切,记动圆的圆心P的轨迹为曲线W。
相切,记动圆的圆心P的轨迹为曲线W。
(1)求曲线W的方程;
(2)过点F作互相垂直的直线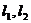 ,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
(3)分别在A、B两点作曲线W的切线,这两条切线的交点记为Q。
求证:QA⊥QB,且点Q在某一定直线上。
科目:gzsx 来源:甘肃省兰州五十五中2011-2012学年高三第一次月考试题数学理 题型:解答题
设点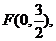 动圆P经过点F且和直线
动圆P经过点F且和直线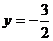 相切,记动圆的圆心P的轨迹为曲线W。
相切,记动圆的圆心P的轨迹为曲线W。
(1)求曲线W的方程;
(2)过点F作互相垂直的直线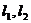 ,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
(3)分别在A、B两点作曲线W的切线,这两条切线的交点记为Q。
求证:QA⊥QB,且点Q在某一定直线上。
科目:gzsx 来源: 题型:
科目:gzsx 来源:2010-2011学年安徽省六安一中高三(下)第六次月考数学试卷(文科)(解析版) 题型:解答题
科目:gzsx 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
科目:gzsx 来源: 题型:解答题
设抛物线的顶点在原点,准线方程为x=- .
.
(1)求抛物线的标准方程;
(2)若点P是抛物线上的动点,点P在y轴上的射影是Q,点M ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
(3)过抛物线焦点F作互相垂直的两直线分别交抛物线于A,C,B,D,求四边形ABCD面积的最小值.
科目:gzsx 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集14讲练习卷(解析版) 题型:解答题
设抛物线的顶点在原点,准线方程为x=-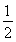 .
.
(1)求抛物线的标准方程;
(2)若点P是抛物线上的动点,点P在y轴上的射影是Q,点M ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
(3)过抛物线焦点F作互相垂直的两直线分别交抛物线于A,C,B,D,求四边形ABCD面积的最小值.
科目:gzsx 来源:不详 题型:解答题
 .
. ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;