已知:如图.在△ABC中.∠ACB=90°.D,E是边AB上的两点答案解析
科目:czsx
来源:
题型:
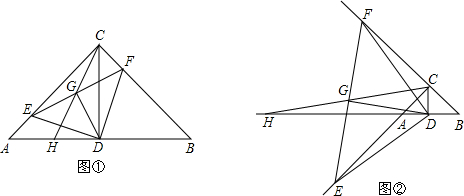
已知,△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是射线CA上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.
(1)如图①,若E在边AC上.试说明:①AE=CF; ②CG=GD;
(2)如图②,若E在边CA的延长线上.(1)中的两个结论是否仍成立?(直接写出成立结论的序号,不要说明理由)
(3)若AE=3,CH=5,求边AC的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知,△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是射线CA上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.
(1)如图①,若E在边AC上.试说明:①AE=CF; ②CG=GD;
(2)如图②,若E在边CA的延长线上.(1)中的两个结论是否仍成立?(直接写出成立结论的序号,不要说明理由)
(3)若AE=3,CH=5,求边AC的长.

查看答案和解析>>
科目:czsx
来源:2015-2016学年江苏省盐城市八年级上第三次调研数学试卷(解析版)
题型:解答题
已知,△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是射线CA上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.
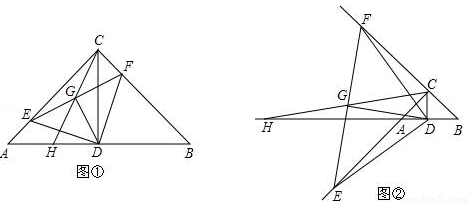
(1)如图①,若E在边AC上.试说明:①AE=CF; ②CG=GD;
(2)如图②,若E在边CA的延长线上.(1)中的两个结论是否仍成立?(直接写出成立结论的序号,不要说明理由)
(3)若AE=3,CH=5,求边AC的长.
查看答案和解析>>
科目:czsx
来源:
题型:
已知,如图,在 Rt△ABC 中,∠ACB=90°,AC=BC,点 E、F 分别是斜边 AB 上的两点,且∠FCE=45°.
(1)现将 CF 绕点 C 顺时针旋转 90°到 CD,连结 AD.求证:AD=BF. 若 EF=10,BF=8.求 AE 的长及△ABC 的面积.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
18.

已知,如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E、F分别是斜边AB上的两点,且∠FCE=45°.
(1)现将CF绕点C顺时针旋转90°到CD,连结AD.求证:AD=BF.
(2)若EF=10,BF=8.求AE的长及△ABC的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
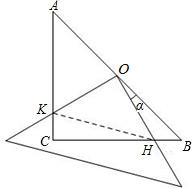
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CHK的面积为
时,求出x的值.
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
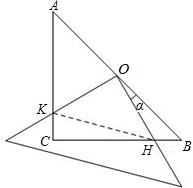 已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CHK的面积为 时,求出x的值.
时,求出x的值.
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年浙江省省一级重点中学自主招生考试数学模拟试卷(解析版)
题型:解答题
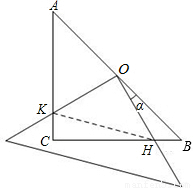
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CHK的面积为

时,求出x的值.
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
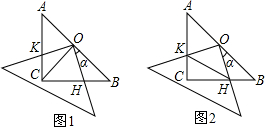
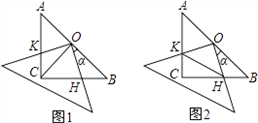
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度反(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度反(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.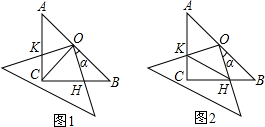
查看答案和解析>>
科目:czsx
来源:四川省期中题
题型:解答题
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点D处,两直角边分别经过点B、C,然后将三角板绕点D按顺时针方向旋转一个角度α(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.
查看答案和解析>>
科目:czsx
来源:2010年甘肃省定西市安定区新集初中九年级数学竞赛试卷(解析版)
题型:解答题
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度反(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度反(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.

查看答案和解析>>
科目:czsx
来源:黑龙江省期末题
题型:解答题
如图所示,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,以斜边AB为直径作圆M,已知OA=1,且OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根。
(1)求OB的长。
(2)分别求出点M和点C的坐标。
(3)在圆M上,是否存在一点P(P不与C重合),使△ABP与△ABC全等?若存在,请直接写出P点的坐标;若不存在,说明理由。
查看答案和解析>>
科目:czsx
来源:
题型:解答题
5.已知△ABC≌△DEF,在△ABC中,∠ACB=90°,BC=3,AC=4.现将这两个全等的直角三角形按图①所示位置摆放,点A与点E重合,直角边AC与EF在同一直线上,如图②,现固定△ABC,将△DEF沿射线AC方向平行移动,运动过程中,直线DE与直线AB交于点M,点N是线段AC的中点,当点E运动到点N时停止运动.设AM=x.

(1)如图①,求点A与点E重合时两三角形重叠部分的面积;
(2)在△DEF运动过程中,△AMN能不能是以MN为腰的等腰三角形?若不能,请说明理由;若能,求出对应的x的值;
(3)在△DEF运动过程中,设两个三角形重叠部分面积为y,直接写出y与x的函数解析式及对应的x的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
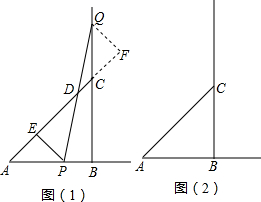
(1)等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,过P作PE⊥AC于点E.设P点运动时间为t.
①当点P在线段AB上运动时,线段DE的长度是否改变?若不改变,求出DE的值;若改变,请说明理由.
下面给出一种解题的思路,你可以按这一思路解题,也可以选择另外的方法解题.
解:过Q作QF⊥直线AC于点M
∵PE⊥AC于点E,QF⊥直线AC于点M
∴∠AEP=∠F=90°
(下面请你完成余下的解题过程)
②当点P在线段AB的延长线上运动时,(1)中的结论是否还成立?请在图2画出图形并说明理由.
(2)若将(1)中的“腰长为10cm的等腰直角△ABC”改为“边长为a的等边△ABC”时(其余条件不变),则线段DE的长度又如何?(直接写出答案,不需要解题过程)
(3)若将(2)中的“等边△ABC”改为“△ABC”(其余条件不变),请你做出猜想:当△ABC满足
∠A=∠ACB
∠A=∠ACB
条件时,(2)中的结论仍然成立.(直接写出答案,不需要解题过程)
查看答案和解析>>
科目:czsx
来源:
题型:
已知,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
(1)如图1,求证:CD⊥AB;
(2)请写出你在(1)的证明过程中应用的两个互逆的真命题;
(3)将△ADC沿CD所在直线翻折,A点落在BD边所在直线上,记为A′点,
①如图2,若∠B=34°,求∠A′CB的度数;
②若∠B=n°,请直接写出∠A′CB的度数(用含n的代数式表示).
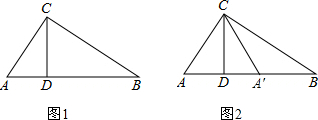
查看答案和解析>>
科目:czsx
来源:
题型:
已知,如图,Rt△ABC中,∠ACB=90°,AB=5,两直角边AC、BC的长是关于x的方程x
2-(m+5)x
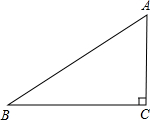
+6m=0的两个实数根.
(1)求m的值及AC、BC的长(BC>AC);
(2)在线段BC的延长线上是否存在点D,使得以D、A、C为顶点的三角形与△ABC相似?若存在,求出CD的长;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
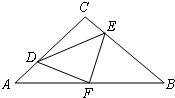
如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,给出以下个结论:
①CD=BE;②四边形CDFE不可能是正方形;③△DFE是等腰直角三角形;
④
S四边形CDFE=S△ABC.当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),上述结论中始终正确的有( )
查看答案和解析>>
科目:czsx
来源:
题型:
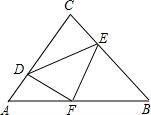
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
①CD=BE
②四边形CDFE不可能是正方形
③△DEF是等腰直角三角形
④
S四边形CDFE=S△ABC.当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),
上述结论中始终正确的有
①③④
①③④
.
查看答案和解析>>





 已知,如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E、F分别是斜边AB上的两点,且∠FCE=45°.
已知,如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E、F分别是斜边AB上的两点,且∠FCE=45°. 已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中: 已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中: 时,求出x的值.
时,求出x的值. 时,求出x的值.
时,求出x的值.






 (1)等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,过P作PE⊥AC于点E.设P点运动时间为t.
(1)等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,过P作PE⊥AC于点E.设P点运动时间为t.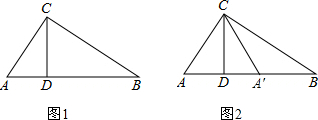
 +6m=0的两个实数根.
+6m=0的两个实数根. 如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,给出以下个结论:
如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,给出以下个结论: 如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论: