
科目:czsx 来源:2015年初中毕业升学考试(福建漳州卷)数学(解析版) 题型:解答题
(12分)理数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路: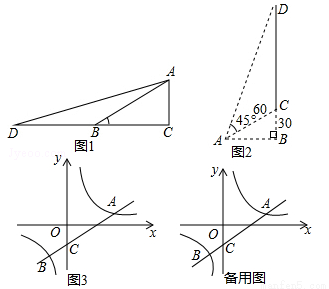
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC= .tanD=tan15°=
.tanD=tan15°=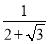 =
=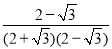 =
= .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=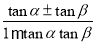 .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=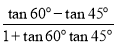 =
=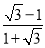 =
= .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线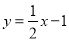 与双曲线
与双曲线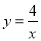 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
科目:czsx 来源: 题型:

| 1 | 2 |
科目:czsx 来源: 题型:解答题
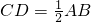 ,你能用矩形的性质说明这个结论吗?请说明.
,你能用矩形的性质说明这个结论吗?请说明.科目:czsx 来源: 题型:解答题

科目:czsx 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:解答题
阅读下面材料:
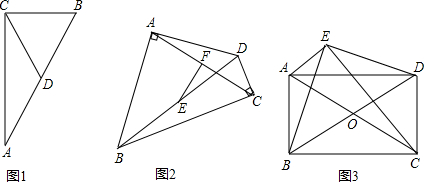
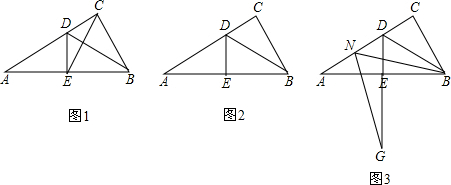
(1)小乔遇到了这样一个问题:如图1,在Rt△ABC中,∠C=90°,D,E分别为CB,CA边上的点,且AE=BC,BD=CE,BE与AD的交点为P,求∠APE的度数;
小乔发现题目中的条件分散,想通过平移变换将分散条件集中,如图2,过点B作BF//AD且BF=AD,连接EF,AF,从而构造出△AEF与△CBE全等,经过推理和计算能够使问题得到解决(如图2).请回答:∠APE的度数为___________________.
参考小乔同学思考问题的方法,解决问题:
(2)如图3,AB为⊙O的直径,点C在⊙O上,D、E分别为CB,CA上的点,且AE= BC,BD=
BC,BD= CE,BE与AD交于点P,在图3中画出符合题意的图形,并求出sin∠APE的值.
CE,BE与AD交于点P,在图3中画出符合题意的图形,并求出sin∠APE的值.
科目:czsx 来源: 题型:
科目:czsx 来源:2012-2013学年北京市西城区(北区)八年级上学期期末考试数学试卷(带解析) 题型:解答题
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.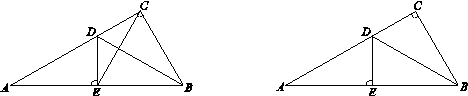
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,且MB=MG.试探究ND,DG与AD数量之间的关系,并说明理由.
科目:czsx 来源:2012-2013学年北京市西城区(北区)八年级上学期期末考试数学试卷(解析版) 题型:解答题
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.
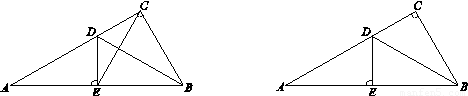
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,且MB=MG.试探究ND,DG与AD数量之间的关系,并说明理由.
科目:czsx 来源: 题型:解答题
科目:czsx 来源:不详 题型:解答题
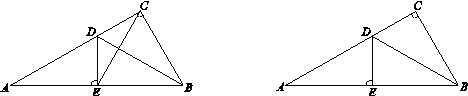
科目:czsx 来源: 题型:
如下图所示,在Rt△ABC中,∠C=90℃,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中不一定相等的线段有( )
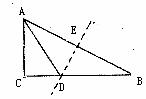
A.AC=AE=BE B.AD=BD C.AC=BD D.CD=DE
科目:czsx 来源: 题型:
如下图所示,在Rt△ABC中,∠C=90℃,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中不一定相等的线段有( )
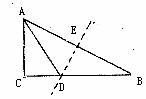
A.AC=AE=BE B.AD=BD C.AC=BD D.CD=DE
科目:czsx 来源:2014-2015学年北京市八年级上学期期中检测数学试卷(解析版) 题型:解答题
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.

(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
科目:czsx 来源: 题型:
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.



科目:czsx 来源:2015-2016学年江苏省八年级上12月月考数学卷(解析版) 题型:解答题
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.

(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
科目:czsx 来源: 题型:解答题
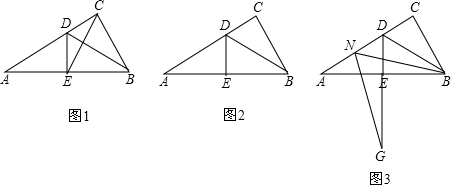
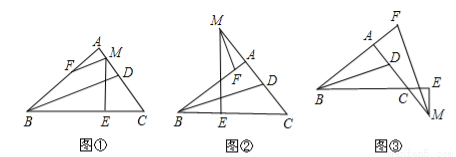
小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.
我选图 来证明.
科目:czsx 来源:不详 题型:解答题

科目:czsx 来源:2016届江苏省无锡市崇安区七年级下学期期中统考数学试卷(解析版) 题型:解答题
小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.
我选图 来证明.
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.

(1)如图①,M为边AC上一点,则BD、MF的位置关系是  ;
;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线 上一点,则BD、MF的位置关系是 ;
上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.
我选图 来证明.