
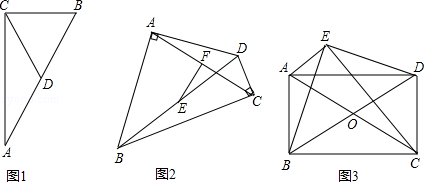
���� ��1���ӳ�CD����E��ʹCD=DE������AE��BE��Ȼ��֤���ı���AEBC�Ǿ��Σ��ٸ��ݾ��ε����ʿɵ�CD=$\frac{1}{2}$AB��
��2��EF��AC������AE��CE��Ȼ����ݣ�1���еĽ��۵õ�AE=CE���ٸ��ݵ��������ε����ʿɵ�EF��AC��
��3������EO�����ݣ�1���еĽ��ۿɵ�OE=$\frac{1}{2}$DB��OE=$\frac{1}{2}$AC�������õ�AC=BD�����ݶԽ�����ȵ�ƽ���ı����Ǿ��οɵý��ۣ�
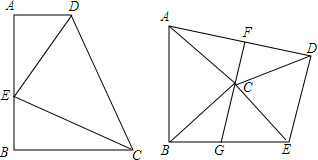
��� ֤������1����ͼ1���ӳ�CD����E��ʹCD=DE��
����AE��BE��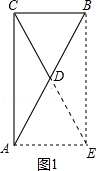
��CD=DE����DΪAB�е㣬
���ı���AEBCΪƽ���ı��Σ�
�ߡ�ACB=90�㣬
��ƽ���ı���AEBC�Ǿ��Σ�
��CE=AB��
��CD=$\frac{1}{2}$CE��
��CD=$\frac{1}{2}$AB��
��2��EF��AC���������£�
��ͼ2������AE��CE��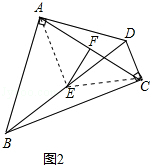
�ߡ�BAD=90�㣬EΪBD�е㣬
��AE=$\frac{1}{2}$DB��
�ߡ�DCB=90�㣬
��CE=$\frac{1}{2}$BD��
��AE=CE��
��F��AC�е㣬
��EF��AC��
��3����ͼ3������EO��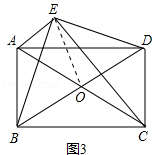
���ı���ABCDΪƽ���ı��Σ�
��O��ΪAC��BD�е㣬
�ߡ�AEC=90�㣬OΪAC�е㣬
��$OE=\frac{1}{2}AC$��
�ߡ�BED=90�㣬OΪBD�е㣬
��EO=$\frac{1}{2}$BD��
��AC=BD��
�֡��ı���ABCDΪƽ���ı��Σ�
���ı���ABCD�Ǿ��Σ�
���� ������Ҫ�����˾��ε��ж������ʣ��ؼ��Ǹ��ݶԽ�����ȵ�ƽ���ı����Ǿ���֤���ı���AEBC�Ǿ��Σ�ͬʱ���վ��εĶԽ�������һ���ƽ�֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2m-4 | B�� | 2m-2n-4 | C�� | 2m-2n+4 | D�� | 4m-2n+4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com