如图.在abcd中.点e为边cd的中点.连接ae答案解析

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：解答题

8．已知正方形ABCD，点M为边AB的中点．
（1）如图1，点G为线段CM上的一点，且∠AGB=90°，延长AG、BG分别与边BC、CD交于点E、F．
①求证：BE=CF；
②求证：BE²=BC•CE．
（2）如图2，在边BC上取一点E，满足BE²=BC•CE，连接AE交CM于点G，连接BG并延长交CD于点F，求tan∠CBF的值．

科目：czsx 来源： 题型：解答题

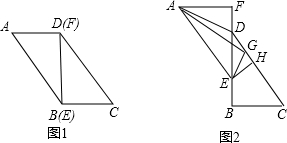
18．如图1，在平行四边形ABCD中，连接BD，AD=6cm，BD=8cm，∠DBC=90°，现将△AEF沿BD的方向匀速平移，速度为2cm/s，同时，点G从点D出发，沿DC的方向匀速移动，速度为2cm/s．当△AEF停止移动时，点G也停止运动，连接AD，AG，EG，过点E作EH⊥CD于点H，如图2所示，设△AEF的移动时间为t（s）（0＜t＜4）．
（1）当t=1时，求EH的长度；
（2）若EG⊥AG，求证：EG²=AE•HG；
（3）设△AGD的面积为y（cm²），当t为何值时，y可取得最大值，并求y的最大值．

科目：czsx 来源： 题型：解答题

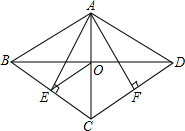
20．如图 在▱ABCD中 对角线AC、BD 相交于点O，AE⊥BC，AF⊥CD，垂足分别是E、F，点E、F恰好为BC、CD的中点，连接OE．
（1）▱ABCD是什么特殊四边形？请证明你的结论．
（2）求∠AEO的度数．

科目：czsx 来源： 题型：解答题

15．阅读与理解：
如图①，AD是△ABC中BC边上的中线，利用“等底同高的三角形面积相等”可以得出：S_△ABD=S_△ACD=0.5S_△ABC．即：三角形的中线的性质：三角形的中线等分三角形的面积．
操作与探索：
（1）如图②，△ABC的面积为a．分别延长BC到点D，延长CA到点E，延长AB到点F，使CD=BC，AE=CA，BF=AB，连接DE、EF、FD．则△DEF的面积为7a（用含a的代数式表示）．
（2）如图③，四边形ABCD的面积是m，E、F、G、H分别是AB、BC、CD、AD的中点，则图中阴影部分的面积是$\frac{1}{2}$m（用含m的代数式表示）．
拓展与应用：
如图④，把等腰梯形ABCD放在平面直角坐标系中，已知三个顶点的坐标分别是A（-2，0）、B（6，0）、C（4，4），画出经过顶点D并且平分梯形面积的直线，并求出它的解析式．

科目：czsx 来源：吉林省中考真题 题型：解答题

如图，ABCD中，∠BAD=32°，分别以BC、CD为边向外作△BCE和△DCF，使BE=BC，DF=DC，∠EBC=∠CDF，延长AB交边EC于点H，点H在E、C两点之间，连接AE、AF。
（1）求证：△ABE≌△FDA；
（2）当AE⊥AF时，求∠EBH的度数。

科目：czsx 来源：2016届江苏省九年级上学期第二次月考数学试卷（解析版） 题型：解答题

科目：czsx 来源： 题型：解答题

13．如图，正方形ABCD的边CD与Rt△EFG的直角边EF重合，将正方形ABCD以1cm/s的速度沿FE方向移动，在移动过程中，边CD始终与边EF重合（移动开始时点C与点F重合）．连接AE，过点C作AE的平行线交直线EG于点H，连接HD．已知正方形ABCD的边长为1cm，EF=4cm，设正方形移动时间为x（s），线段EH的长为y（cm），其中0≤x≤2.5．
（1）当x=2时，AE的长为$\sqrt{2}$cm；
（2）试求出y关于x的函数关系式，并求出△EHD与△ADE的面积之差；
（3）当正方形ABCD移动时间x=$\frac{5-\sqrt{5}}{2}$时，线段HD所在直线经过点B．

科目：czsx 来源： 题型：解答题

7．在平行四边形ABCD中，点E在CD上，点F在AB上，连接AE、CF、DF、BE，∠DAE=∠BCF．

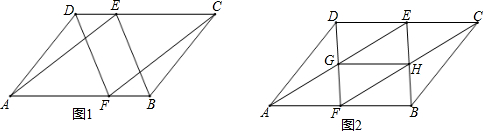
（1）如图1，求证：四边形DFBE是平行四边形；
（2）如图2，若E是CD的中点，连接GH，在不添加任何辅助线的情况下，请直接写出图2中以GH为边或以GH为对角线的所有平行四边形．

科目：czsx 来源： 题型：解答题

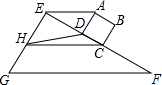
11．如图，正方形ABCD的边CD与Rt△EFG的直角边EF重合，将正方形ABCD以1cm/s的速度沿FE方向移动，在移动过程中，边CD始终与边EF重合（移动开始时点C与点F重合）．连接AE，过点C作AE的平行线交直线EG于点H，连接HD．已知正方形 ABCD 的边长为1cm，EF=4cm，设正方形移动时间为x（s），线段EH的长为y（cm），其中0≤x≤2.5．
（1）当x=2时，AE的长为$\sqrt{2}$；
（2）试求出y关于x的函数关系式，并结合图形直接写出点H在直线EG上运动的长度；
（3）当线段HD所在直线经过点B时，求线段HD的长．

科目：czsx 来源： 题型：解答题

1．在四边形ABCD中，点E在CD的延长线上，CE=BD，连接AE，∠ABD的平分线与AE相交于点F．
（1）如图1，当四边形ABCD为正方形时，求∠AFB的度数；
（2）如图2，当四边形ABCD为平行四边形时，延长BF，CE，它们相交于点K，求证：BF=KF．

科目：czsx 来源： 题型：解答题

11．在矩形ABCD中，AD=3，CD=4，点E在边CD上，且DE=1．

感知：如图①，连接AE，过点E作EF⊥AE，交BC于点F，连接AF，易证：△ADE≌△ECF（不需要证明）；
探究：如图②，点P在矩形ABCD的边AD上（点P不与点A、D重合），连接PE，过点E作EF⊥PE，交BC于点F，连接PF．求证：△PDE∽△ECF；
应用：如图③，若EF交AB边于点F，其他条件不变，且△PEF的面积是3，则AP的长为2．

科目：czsx 来源： 题型：解答题

13．（1）如图（1），在四边形ABCD中，AB∥CD，如果延长DC到点E，使CE=AB，连接AE，那么有S_{四边形ABCD=}S_△ADE，作DE边中点P，连接AP，则AP所在直线为四边形ABCD的面积等分线，你能说明理由吗？
（2）如图（2），如果四边形ABCD中，AB与CD不平行，且S_△ADC＞S_△ABC，过点A能否作出四边形ABCD的面积等分线？若能，请画出面积等分线，并简单说明作图过程．

科目：czsx 来源： 题型：解答题

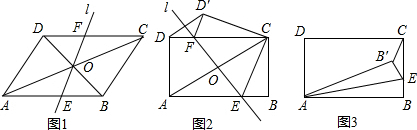
4．（1）如图1，在平行四边形ABCD中，对角线AC、BD相交于O点，过点O的直线1与边AB、CD分别交于点E、F，绕点O旋转直线1，猜想直线1旋转到什么位置时，四边形AECF是菱形．证明你的猜想；
（2）若将（1）中四边形ABCD改成矩形ABCD，使AB=4，BC=3．
①如图2，绕点O旋转直线1与边AB、CD分别交于点E、F，将矩形ABCD沿EF折叠，当点A与点C重合时，点D的对应点为D′，连接DD′，求线段DF的长；
②如图3，绕点O继续旋转直线1，使直线1与边BC或BC的延长线交于点E，连接AE，将矩形ABCD沿AE折叠，点B的对应点为B′，连接CB′得到△CEB′，当△CEB′为直角三角形时，请直接写出满足条件的线段CE的长．

科目：czsx 来源： 题型：解答题

7．（1）如图1，在平行四边形ABCD中，对角线AC、BD相交于O点，过点O的直线l与边AB、CD分别交于点E、F，绕点O旋转直线l，猜想直线l旋转到什么位置时，四边形AECF是菱形．证明你的猜想．
（2）若将（1）中四边形ABCD改成矩形ABCD，使AB=4cm，BC=3cm，
①如图2，绕点O旋转直线l与边AB、CD分别交于点E、F，将矩形ABCD沿EF折叠，使点A与点C重合，点D的对应点为D′，连接DD′，求△DFD′的面积．
②如图3，绕点O继续旋转直线l，直线l与边BC或BC的延长线交于点E，连接AE，将矩形ABCD沿AE折叠，点B的对应点为B′，当△CEB′为直角三角形时，求BE的长度．请直接写出结果，不必写解答过程．

科目：czsx 来源： 题型：解答题

1．材料：相似三角形的对应边的比相等，对应角相等．
（1）如图①，△ABC中，∠A=50°，∠B=45°，点D、E分别在AB、AC上，且AD•AB=AE•AC．则△ABC与△ADE的关系为△ABC∽△AED，∠ADE=85°；
（2）如图②，在平行四边形ABCD中，对角线AC、BD交于点O，M为AD中点，连接CM交BD于点N，且ON=1，求BD的长；
（3）△ABC中，∠A=25°，CD是边AB上的高，且CD²=AD•BD，请直接写出∠ABC的度数．

科目：czsx 来源： 题型：

如图在平行四边形ABCD中，点E在AD边上，AE=

1

2

DE，连接AC与BE交于点P，若点Q为CD的中点，则S_△APE：S_{四边形PQDE}

 

．

科目：czsx 来源： 题型：

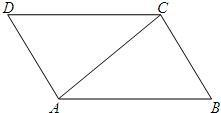
如图，AC是平行四边形ABCD的对角线．
（1）请按如下步骤在图中完成作图（保留作图痕迹）：
①分别以A，C为圆心，以大于

1

2

AC长为半径画弧，弧在AC两侧的交点分别为P，Q．
②连接PQ，PQ分别与AB，AC，CD交于点E，O，F；
（2）求证：AE=CF．

科目：czsx 来源： 题型：

如图，正方形ABCD的边长是4，M是AD的中点．动点E在线段AB上运动．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．
（1）求证：△GEF是等腰三角形；
（2）设AE=x时，△EGF的面积为y．求y关于x的函数关系式，并写出自变量x的取值范围；
（3）在点E运动过程中△GEF是否可以成为等边三角形？请说明理由．