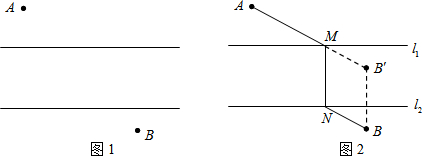科目:czsx 来源:2013年贵州省黔南州惠水县摆金中学中考数学模拟试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:选择题
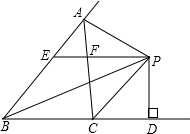 如图,△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,过点P作BC的平行线交AB,AC分别于点E,F,作PD⊥BC于点D.给出下列三个结论:
如图,△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,过点P作BC的平行线交AB,AC分别于点E,F,作PD⊥BC于点D.给出下列三个结论:| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
科目:czsx 来源: 题型:
 26、如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
26、如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.科目:czsx 来源: 题型:解答题
 x+12分别与x轴、y轴交于点A、B,经过点B直
x+12分别与x轴、y轴交于点A、B,经过点B直 线y=kx+12交x轴于点C,且AB=AC.
线y=kx+12交x轴于点C,且AB=AC.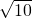 :10?
:10?科目:czsx 来源:2012年黑龙江省哈尔滨市香坊区中考数学三模试卷(解析版) 题型:解答题
 x+12分别与x轴、y轴交于点A、B,经过点B直线y=kx+12交x轴于点C,且AB=AC.
x+12分别与x轴、y轴交于点A、B,经过点B直线y=kx+12交x轴于点C,且AB=AC.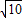 :10?
:10?
科目:czsx 来源:2013年初中毕业升学考试(山东青岛卷)数学(解析版) 题型:解答题
已知,如图, ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
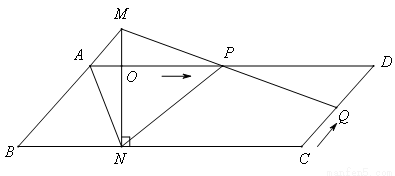
(1)当t为何值时,四边形AQDM是平行四边形?
(2)设四边形ANPM的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM的面积是 ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
(4)连接AC,是否存在某一时刻t,使NP与AC的交点把线段AC分成 的两部分?若存在,求出相应的t值,若不存在,说明理由
的两部分?若存在,求出相应的t值,若不存在,说明理由
科目:czsx 来源: 题型:解答题
已知,如图,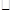 ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题: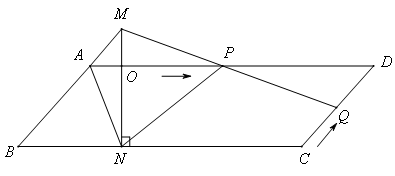
(1)当t为何值时,四边形AQDM是平行四边形?
(2)设四边形ANPM的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM的面积是 ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
(4)连接AC,是否存在某一时刻t,使NP与AC的交点把线段AC分成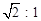 的两部分?若存在,求出相应的t值,若不存在,说明理由
的两部分?若存在,求出相应的t值,若不存在,说明理由
科目:czsx 来源:2013年山东省青岛市中考数学试卷(解析版) 题型:解答题
 已知:如图,▱ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
已知:如图,▱ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1) 的两部分?若存在,求出相应的t值;若不存在,说明理由.
的两部分?若存在,求出相应的t值;若不存在,说明理由.科目:czsx 来源:不详 题型:解答题
 ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
 ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由 的两部分?若存在,求出相应的t值,若不存在,说明理由
的两部分?若存在,求出相应的t值,若不存在,说明理由科目:czsx 来源: 题型:解答题
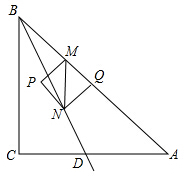 如图,在△ABC中,∠C=90°,AC=BC=4,D为AC中点,M为线段AB上一动点(M不与A、B重合),过点M作BC的平行线交BD于点N,以MN为对角线作正方形MPNQ,设MN的长为m.
如图,在△ABC中,∠C=90°,AC=BC=4,D为AC中点,M为线段AB上一动点(M不与A、B重合),过点M作BC的平行线交BD于点N,以MN为对角线作正方形MPNQ,设MN的长为m.科目:czsx 来源: 题型:
| 4 |
| 3 |
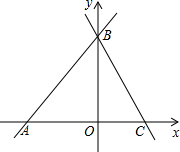 线y=kx+12交x轴于点C,且AB=AC.
线y=kx+12交x轴于点C,且AB=AC.| 10 |
科目:czsx 来源: 题型:解答题
 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度为每秒1个单位长度,当Q点运动到A点,P、Q两点同时停止运动,设点Q运动的时间为t秒.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度为每秒1个单位长度,当Q点运动到A点,P、Q两点同时停止运动,设点Q运动的时间为t秒.科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
 (2013•青岛)已知:如图,▱ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
(2013•青岛)已知:如图,▱ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)| 2 |
科目:czsx 来源: 题型:
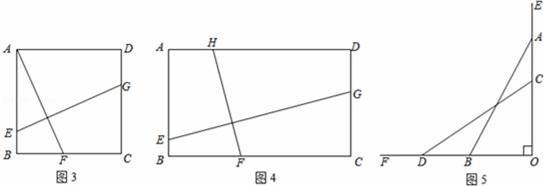
如图1,A、B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)


【问题解决】
如图2,过点B作BB′⊥l2,且BB′等于河宽,连接AB′交l1于点M,作MN⊥l1交l2于点N,则MN就为桥所在的位置.
【类比联想】
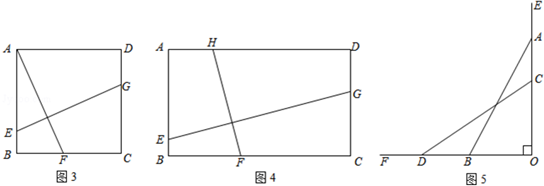
(1)如图3,正方形ABCD中,点E、F、G分别在AB、BC、CD上,且AF⊥GE,求证:AF=EG.
(2)如图4,矩形ABCD中,AB=2,BC=x,点E、F、G、H分别在AB、BC、CD、AD上,且EG⊥HF,设y=
 ,试求y与x的函数关系式.
,试求y与x的函数关系式.
【拓展延伸】
如图5,一架长5米的梯子斜靠在竖直的墙面OE上,初始位置时OA=4米,由于地面OF较光滑,梯子的顶端A下滑至点C时,梯子的底端B左滑至点D,设此时AC=a米,BD=b米.
(3)当a= 1 米时,a=b.
(4)当a在什么范围内时,a<b?请说明理由.

科目:czsx 来源: 题型:

科目:czsx 来源: 题型:解答题
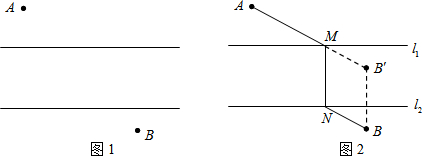

科目:czsx 来源: 题型:

| HF |
| EG |

科目:czsx 来源: 题型:解答题
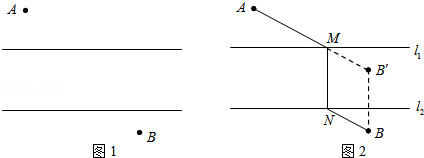
科目:czsx 来源: 题型:解答题