
科目:czsx 来源: 题型:解答题
 如图,在以AB为直径的⊙O中,过点A作⊙O的切线,点C为切线上一点,连接BC交⊙O于点M,过点M作⊙O的切线交AC于点N,连接ON.
如图,在以AB为直径的⊙O中,过点A作⊙O的切线,点C为切线上一点,连接BC交⊙O于点M,过点M作⊙O的切线交AC于点N,连接ON.科目:czsx 来源: 题型:
| 1 |
| 3 |
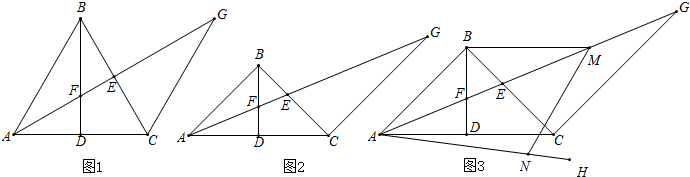
科目:czsx 来源: 题型:
 如图△ABC中M为BC的中点,N为AM上一点,过N作直线PQ分别交线段AB、AC于P、Q.
如图△ABC中M为BC的中点,N为AM上一点,过N作直线PQ分别交线段AB、AC于P、Q.| PB |
| PA |
| QC |
| QA |
| MN |
| NA |
科目:czsx 来源:期末题 题型:解答题
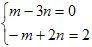 ,x,y满足
,x,y满足 +(y+5)2=0.
+(y+5)2=0.
科目:czsx 来源: 题型:单选题
 如图所示,△ABC中,AB=10cm,AC=8cm,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为
如图所示,△ABC中,AB=10cm,AC=8cm,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为科目:czsx 来源: 题型:
 如图,已知△ABC中,BD平分∠ABC,点M是线段BD上一点,过M点作EF∥BC,分别交边AB、AC于点E、F,作MN∥AB交BC于点N.
如图,已知△ABC中,BD平分∠ABC,点M是线段BD上一点,过M点作EF∥BC,分别交边AB、AC于点E、F,作MN∥AB交BC于点N.科目:czsx 来源: 题型:选择题
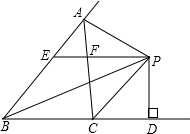 如图,△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,过点P作BC的平行线交AB,AC分别于点E,F,作PD⊥BC于点D.给出下列三个结论:
如图,△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,过点P作BC的平行线交AB,AC分别于点E,F,作PD⊥BC于点D.给出下列三个结论:| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
科目:czsx 来源: 题型:填空题
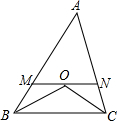 如图,△ABC中,AB=8,AC=6,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为14.
如图,△ABC中,AB=8,AC=6,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为14. 科目:czsx 来源: 题型:
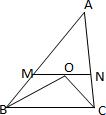 18、如图所示,△ABC中,AB=10cm,AC=8cm,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为( )
18、如图所示,△ABC中,AB=10cm,AC=8cm,∠ABC和∠ACB的角平分线交于点O,过点O作BC的平行线MN交AB于点M,交AC于点N,则△AMN的周长为( )科目:czsx 来源:江苏省无锡市惠山区2012届九年级下学期期中考试数学试题 题型:022
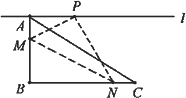
如图在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、AC边上(包括端点)移动,则线段AP长度的最大值与最小值的差为________.
科目:czsx 来源: 题型:
如图在三角形纸片ABC中,已知∠ABC=90º,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、AC边上移动,则线段AP长度的最大值与最小值的差为 .

科目:czsx 来源:2013年中考数学解密预测试卷(二)(解析版) 题型:填空题

科目:czsx 来源:2012年广东省广州市名校中考数学模拟试卷(解析版) 题型:填空题

科目:czsx 来源:2012年江苏省无锡市惠山区中考数学一模试卷(解析版) 题型:填空题

科目:czsx 来源:2012年河南省中招考试说明解密预测数学试卷(五)(解析版) 题型:填空题

科目:czsx 来源:江苏期中题 题型:填空题

科目:czsx 来源: 题型:
 如图,在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上(包括端点)移动,则线段AP长度的最大值与最小值的差为( )
如图,在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上(包括端点)移动,则线段AP长度的最大值与最小值的差为( )科目:czsx 来源: 题型:单选题
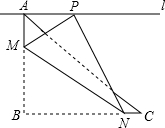 如图,在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上(包括端点)移动,则线段AP长度的最大值与最小值的差为
如图,在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN,当点P在直线l上移动时,折痕的端点M、N也随之移动,若限定端点M、N分别在AB、BC边上(包括端点)移动,则线段AP长度的最大值与最小值的差为

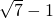
科目:czsx 来源: 题型:解答题
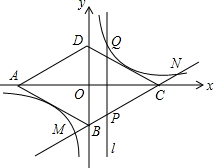 已知菱形ABCD对角线AC=8,BD=4,以AC、BD所在的直线为x轴、y轴建立平面直角坐标系,双曲线y=$\frac{k}{x}$恰好经过DC的中点,过直线BC上的点P作直线l⊥x轴,交双曲线于点Q.
已知菱形ABCD对角线AC=8,BD=4,以AC、BD所在的直线为x轴、y轴建立平面直角坐标系,双曲线y=$\frac{k}{x}$恰好经过DC的中点,过直线BC上的点P作直线l⊥x轴,交双曲线于点Q.科目:czsx 来源: 题型:选择题
 如图,在等腰Rt△ABC中,AB=AC,∠BAC=90°,D为AC上一点,沿BD折叠△ABC,使A点落在BC边上的点E处,M为边BC的中点,MN⊥BD与点H,N在AB边上,连接NE交BD于点G,过点N作BD的平行线交AC于点F,下列结论:①AB=$\sqrt{2}$BN;②四边形DFNG为平行四边形;③△BMN∽△EDG;④AN=DF.其中正确结论的个数是( )
如图,在等腰Rt△ABC中,AB=AC,∠BAC=90°,D为AC上一点,沿BD折叠△ABC,使A点落在BC边上的点E处,M为边BC的中点,MN⊥BD与点H,N在AB边上,连接NE交BD于点G,过点N作BD的平行线交AC于点F,下列结论:①AB=$\sqrt{2}$BN;②四边形DFNG为平行四边形;③△BMN∽△EDG;④AN=DF.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |