如图.点p是圆o外一点.pa切圆o与点a.ab是圆o的直径.答案解析
科目:czsx
来源:
题型:解答题
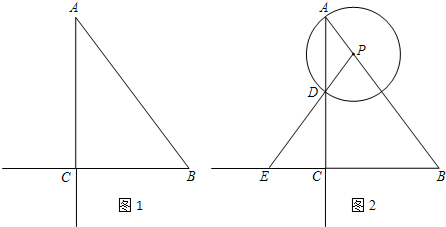
如图1,Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是斜边AB上的一个动点(点P与点A、B不重合),以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,射线PD交射线BC于点E.
(1)如图2,若点E在线段BC的延长线上,设AP=x,CE=y,
①求y关于x的函数关系式,并写出x的取值范围;
②当以BE为直径的圆和⊙P外切时,求AP的长;
(2)设线段BE的中点为Q,射线PQ与⊙P相交于点I,若CI=AP,求AP的长.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
(1)求证:PE=PB;
(2)若AP=2,求CE的长;
(3)当以BE为直径的圆和⊙P外切时,求⊙P的半径.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
(1)若点D是AC的中点,则⊙P的半径为
;
(2)若AP=2,求CE的长;
(3)当以BE为直径的圆和⊙P外切时,求⊙P的半径;
(4)设线段BE的中点为Q,射线PQ与⊙P相交于点I,点P在运动的过程中,能否使点D、C、I、P构成一个平行四边形?若能,请求出AP的长;若不能,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
如图,在Rt△ABC中,∠A CB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
CB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
(1)若点D是AC的中点,则⊙P 的半径为 ;
的半径为 ;
(2)若AP=2,求CE的长;
(3))当以BE为直径的圆和⊙P外切时,求⊙P的半径;
(4)设线段BE的中点为Q,射线PQ与⊙P相交于点I,点P在运动的过程中,能否使点D、C、 I、P构成一个平行四边形?若能,请求出AP的长;若不能,请说明理由。
查看答案和解析>>
科目:czsx
来源:
题型:
(2014•金山区一模)如图1,Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是斜边AB上的一个动点(点P与点A、B不重合),以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,射线PD交射线BC于点E.
(1)如图2,若点E在线段BC的延长线上,设AP=x,CE=y,
①求y关于x的函数关系式,并写出x的取值范围;
②当以BE为直径的圆和⊙P外切时,求AP的长;
(2)设线段BE的中点为Q,射线PQ与⊙P相交于点I,若CI=AP,求AP的长.

查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知P、A、B是x轴上的三点,点A的坐标为(-1,0),点B的坐标为(3,0),且PA:AB=1:2,以AB为直径画⊙M交y轴的正半轴于点C.
(1)求证:PC是⊙M的切线;
(2)在x轴上是否存在这样的点Q,使得直线QC与过A、C、B三点的抛物线只有一个交点?若存在,求点Q的坐标;若不存在,请说明理由;
(3)画⊙N,使得圆心N在x轴的负半轴上,⊙N与⊙M外切、且与直线PC
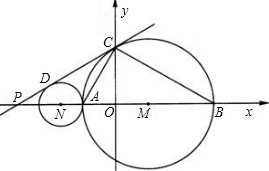
相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么?
查看答案和解析>>
科目:czsx
来源:2013年江西省高级中等学校招生考试数学
题型:044
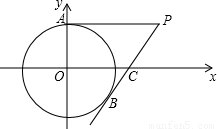
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.

(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,已知P、A、B是x轴上的三点,点A的坐标为(-1,0),点B的坐标为(3,0),且PA:AB=1:2,以AB为直径画⊙M交y轴的正半轴于点C.
(1)求证:PC是⊙M的切线;
(2)在x轴上是否存在这样的点Q,使得直线QC与过A、C、B三点的抛物线只有一个交点?若存在,求点Q的坐标;若不存在,请说明理由;
(3)画⊙N,使得圆心N在x轴的负半轴上,⊙N与⊙M外切、且与直线PC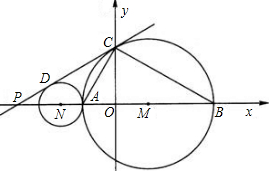 相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么?
相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么?
查看答案和解析>>
科目:czsx
来源:
题型:
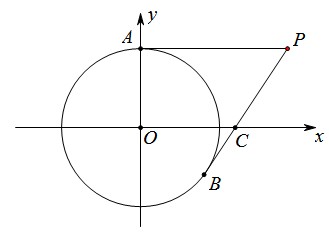
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B ,交x轴于点C.
,交x轴于点C.
(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.
查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(江西卷)数学(解析版)
题型:解答题
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.

(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.
查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(江西南昌卷)数学(解析版)
题型:解答题
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.

(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.
查看答案和解析>>
科目:czsx
来源:2013年江西省中考数学试卷(解析版)
题型:解答题
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.
(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是斜边AB上的一个动点(点P与点A、B不重合),以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,射线PD交射线BC于点E.
(1)如图1,若点E在线段BC的延长线上,设AP=x,CE=y,

①求y关于x的函数关系式,并写出x的取值范围;
②当以BE为直径的圆和⊙P外切时,求AP的长;
(2)设线段BE的中点为Q,射线PQ与⊙P相交于点I,若CI=AP,求AP的长.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.

(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,D点P(2
,2)是⊙O外一点,连接AP,点B从点D出发按逆时针方向以每秒一个单位的速度在⊙O上运动,PB交x轴于点C.
(1)证明PA是⊙O的切线;
(2)当点B在第四象限且PB与⊙O相切时,求点B的坐标;
(3)在(2)的条件下求直线AB的解析式.并直接写出PB与⊙O相切时点B运动的时间.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
20.

如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C
(1)证明PA是⊙O的切线;
(2)求直线AB的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.

如图,已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B是切点,BC是直径,求证:AC∥OP.
证明:连结AB,交OP于点D
∵PA与PB切⊙O于A、B
∴PA=PB,∠1=∠2
∴PD⊥AB,∴∠3=90°
∵BC是⊙O的直径,
∴∠4=90°,∴∠3=∠4,∴AC∥OP
(1)横线上补上应填的条件.
(2)上述证明过程中用到的定理名称或定理的具体内容是(只要求写两个)
①圆周角定理(直径所对的圆周角是直角);②切线长定理(从圆外一点引圆的两条切线,它们的切线长相等,并且这点和圆心的连线平分这两切线的夹角).
查看答案和解析>>
科目:czsx
来源:
题型:
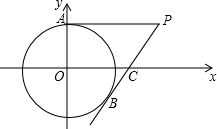
(2013•江西)如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.
(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.
查看答案和解析>>
科目:czsx
来源:2002年全国中考数学试题汇编《二次函数》(05)(解析版)
题型:解答题
(2002•湖州)如图,已知P、A、B是x轴上的三点,点A的坐标为(-1,0),点B的坐标为(3,0),且PA:AB=1:2,以AB为直径画⊙M交y轴的正半轴于点C.
(1)求证:PC是⊙M的切线;
(2)在x轴上是否存在这样的点Q,使得直线QC与过A、C、B三点的抛物线只有一个交点?若存在,求点Q的坐标;若不存在,请说明理由;
(3)画⊙N,使得圆心N在x轴的负半轴上,⊙N与⊙M外切、且与直线PC相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么?
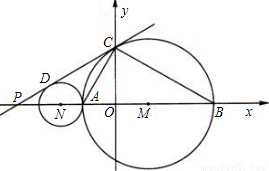
查看答案和解析>>

![]() O1与
O1与![]() O2外切于点P,将三角板的直角顶点放在点P,再将三角板绕点P旋转,使三角板的两直角边中的一边PA与
O2外切于点P,将三角板的直角顶点放在点P,再将三角板绕点P旋转,使三角板的两直角边中的一边PA与![]() O1相交于A,另一边PB与
O1相交于A,另一边PB与![]() O2相交于B(转动中直角边与两圆都不相切),在转动过程中,线段AB的长与半径r之间有什么关系?请说明理由.
O2相交于B(转动中直角边与两圆都不相切),在转动过程中,线段AB的长与半径r之间有什么关系?请说明理由.
![]() O1与
O1与![]() O2的半径不相等,
O2的半径不相等,![]() O1与
O1与![]() O2仍是外切于点P.设
O2仍是外切于点P.设![]() O1的半径为R,
O1的半径为R,![]() O2的半径为r(R>r),重复(1)中的操作过程,观察并分析线段AB与R、r之间有怎样的关系,并说明理由.
O2的半径为r(R>r),重复(1)中的操作过程,观察并分析线段AB与R、r之间有怎样的关系,并说明理由.

 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
 CB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
CB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E. 的半径为 ;
的半径为 ;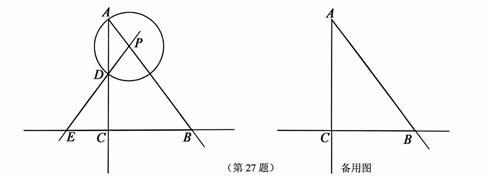

 相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么?
相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么? 
 相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么?
相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么?![]() ,交x轴于点C.
,交x轴于点C.


 如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.


 如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,D点P(2
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,D点P(2 如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C 如图,已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B是切点,BC是直径,求证:AC∥OP.
如图,已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B是切点,BC是直径,求证:AC∥OP. (2013•江西)如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.
(2013•江西)如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.