
科目:czsx 来源: 题型:
 在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.科目:czsx 来源: 题型:解答题
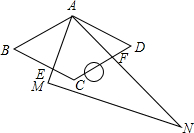 在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.
在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索. 科目:czsx 来源: 题型:解答题
 ,当点Q运动到点B时,停止运动,点P也随之停止.P、Q两点同时出发,设Q运动的时间为t(s).
,当点Q运动到点B时,停止运动,点P也随之停止.P、Q两点同时出发,设Q运动的时间为t(s).科目:czsx 来源:2010年河北省邢台市中考数学二模试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
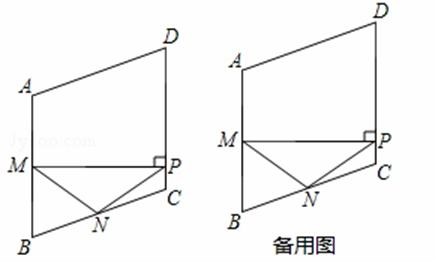
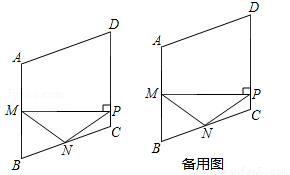
(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
科目:czsx 来源:2016届吉林省长春中考模拟(二)数学试卷(解析版) 题型:解答题
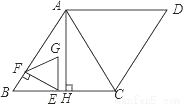
如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.
(1)CE= (含t的代数式表示).
(2)求点G落在线段AC上时t的值.
(3)当S>0时,求S与t之间的函数关系式.
(4)点P在点E出发的同时从点A出发沿A-H-A以每秒2 个单位长度的速度作往复运动,当点E停止运动时,点P随之停止运动,直接写出点P在△EFG内部时t的取值范围.
个单位长度的速度作往复运动,当点E停止运动时,点P随之停止运动,直接写出点P在△EFG内部时t的取值范围.
科目:czsx 来源: 题型:解答题
 如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.
如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.科目:czsx 来源: 题型:解答题
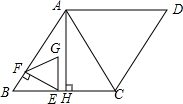
 如图,在菱形ABCD中,AB=6,∠ABC=60°,动点E、F同时从点B出发,其中点E从点B向点A以每秒1个单位的速度运动,点F从点B出发沿B-C-A的路线向终点以每秒2个单位的速度运动,以EF为边向上(或向右)作等边三角形EFG.AH是△ABC中BC边上的高,两点运动时间为t秒,△EFG和△AHC有重合部分时,重合部分图形的周长为L.
如图,在菱形ABCD中,AB=6,∠ABC=60°,动点E、F同时从点B出发,其中点E从点B向点A以每秒1个单位的速度运动,点F从点B出发沿B-C-A的路线向终点以每秒2个单位的速度运动,以EF为边向上(或向右)作等边三角形EFG.AH是△ABC中BC边上的高,两点运动时间为t秒,△EFG和△AHC有重合部分时,重合部分图形的周长为L.科目:czsx 来源: 题型:解答题
 如图,在菱形ABCD中,AB=6,∠ABC=60°,动点E、F同时从顶点B出发,其中点E从点B向点A以每秒1个单位的速度运动,点F从点B出发沿B-C-A的路线向终点A以每秒2个单位的速度运动,以EF为边向上(或向右)作等边三角形EFG,AH是△ABC中BC边上的高,两点运动时间为t秒,△EFG和△AHC的重合部分面积为S.
如图,在菱形ABCD中,AB=6,∠ABC=60°,动点E、F同时从顶点B出发,其中点E从点B向点A以每秒1个单位的速度运动,点F从点B出发沿B-C-A的路线向终点A以每秒2个单位的速度运动,以EF为边向上(或向右)作等边三角形EFG,AH是△ABC中BC边上的高,两点运动时间为t秒,△EFG和△AHC的重合部分面积为S.科目:czsx 来源: 题型:解答题
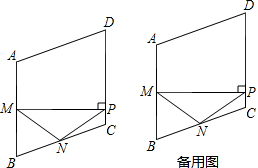
科目:czsx 来源:2015年初中毕业升学考试(福建宁德卷)数学(解析版) 题型:解答题
(13分)如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
科目:czsx 来源: 题型:
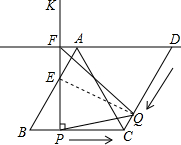 ,当点Q运动到点B时,停止运动,点P也随之停止.P、Q两点同时出发,设Q运动的时间为t(s).
,当点Q运动到点B时,停止运动,点P也随之停止.P、Q两点同时出发,设Q运动的时间为t(s).科目:czsx 来源:北京中考真题 题型:解答题
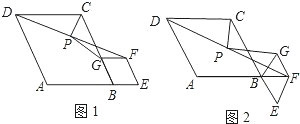
问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连结PG,PC,若∠ABC=∠BEF=60°,探究PG与PC的位置关系及 的值,小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决。 的值,小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决。 |
 |
| 请你参考小聪同学的思路,探究并解决下列问题: |
(1)写出上面问题中线段PG与PC的位置关系及 的值; 的值;(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2),你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明. (3)若图1中∠ABC=∠BEF=2α(0°<α<90°),将菱形BEFG绕点B顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出  的值(用含α的式子表示)。 的值(用含α的式子表示)。 |
科目:czsx 来源: 题型:阅读理解
| PG |
| PC |
| PG |
| PC |
 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出| PG |
| PC |
科目:czsx 来源:2008年北京市初中毕业升学统一考试、数学试卷 题型:044
请阅读下列材料:
问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段a(a+b)(a-b)的中点,连结PG,PC.若∠ABC=∠BEF=60°,探究PG与PC的位置关系及![]() 的值.
的值.
小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.
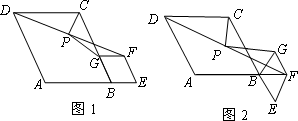
请你参考小聪同学的思路,探究并解决下列问题:
(1)写出上面问题中线段PG与PC的位置关系及![]() 的值;
的值;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(3)若图1中∠ABC=∠BEF=2α(0°<α<90°),将菱形BEFG绕点B顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出![]() 的值(用含α的式子表示).
的值(用含α的式子表示).
科目:czsx 来源: 题型:解答题
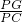 的值.
的值.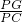 的值;
的值; 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出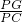 的值(用含α的式子表示).
的值(用含α的式子表示).科目:czsx 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
 的值.
的值. 的值;
的值;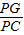 的值(用含α的式子表示).
的值(用含α的式子表示).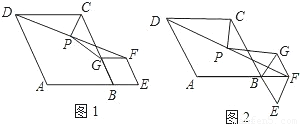
科目:czsx 来源:第7章《锐角三角函数》常考题集(04):7.2 正弦、余弦(解析版) 题型:解答题
 的值.
的值.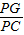 的值;
的值; 的值(用含α的式子表示).
的值(用含α的式子表示).
科目:czsx 来源:第7章《锐角三角函数》中考题集(05):7.2 正弦、余弦(解析版) 题型:解答题
 的值.
的值. 的值;
的值; 的值(用含α的式子表示).
的值(用含α的式子表示).
科目:czsx 来源:第1章《解直角三角形》中考题集(11):1.1 锐角三角函数(解析版) 题型:解答题
 的值.
的值. 的值;
的值; 的值(用含α的式子表示).
的值(用含α的式子表示).