科目：gzsx 来源： 题型：选择题
| A． | k-1 | B． | k | C． | k+1 | D． | $\frac{k（k+1）}{2}$ |
科目：gzsx 来源：不详 题型：单选题
| π |
| 2 |
| A．1 | B．2 | C．3 | D．4 |
科目：gzsx 来源：2006-2007学年浙江省宁波市高一（上）期末数学试卷（解析版） 题型：选择题
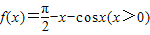在区间[0，2π]内的零点，二分区间[0，2π]的次数为（ ）科目：gzyw 来源： 题型：现代文阅读
科目：xxsx 来源：小学随堂优化作业·四年级数学下册(配人教课标版) 人教课标版 题型：008
数学小法官．(对的用“T”，错的用“F”表示)
0.2米表示1米的十分之二．
科目：xxsx 来源：小学随堂优化作业·四年级数学下册(配人教课标版) 人教课标版 题型：008
数学小法官．(对的用“T”，错的用“F”表示)
小数点左边第二位是百分位．
科目：czsx 来源： 题型：044
数学家高斯在读小学二年级时老师出了这样一道计算题：
1+2+3+4+…+100=?
高斯很快得出了答案，他的计算方法是：
1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=50×(1+100)=5050．
(1)请你应用上述方法求S=1+3+5+…+(2n-1)的计算公式；
(2)如图，第二个图形是由第一个图形中的三角形连接三边中点而得到的，第三个图形是第二个图形中间一个三角形连结三边中点而得到的，依此类推……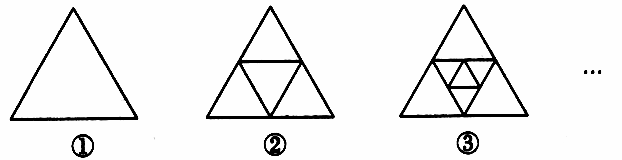
分别写出第二个图形、第三个图形和第四个图形的三角形的个数，由此推测出第n个图形中三角形的个数，并求出第一个图形到第n个图形的三角形个数之和S．
科目：czzz 来源：北京名师导学 （初一） 题型：043
数学家张广厚，考初中时因数学不及格，总分没上线而落榜。他没有气馁，决心学好数学。在补习班补习一年后，他以优秀成绩考上开滦二中（其中数学考了满分）。上中学时，他更注意练数学基本功，成为全校数学尖子，后考入北京大学数学系。上大学后，在一年级他就做了三千道数学分析习题，遇到难题，独立思考，有时憋十多天才做出来。
请结合材料回答：
①张广厚调节不良情绪和培养坚强意志的主要方法与途径分别是什么？
②试分析情绪与意志的关系。
科目：czsx 来源： 题型：解答题
科目：czsx 来源：2007-2008学年江苏省扬州市仪征四中九年级（上）月考数学试卷（解析版） 题型：解答题
科目：xxsx 来源：期末题 题型：判断题
科目：czsx 来源： 题型：
| 1 |
| m |
| 1 |
| m2 |
| 1 |
| m3 |
| 1 |
| mn |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 32 |
| 2 |
| 3 |
| 2 |
| 32 |
| 2 |
| 33 |
| 2 |
| 3n |
| 1 |
| 3n |
| 2 |
| 3 |
| 2 |
| 32 |
| 2 |
| 33 |
| 2 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| 1 |
| 2 |
| 1 |
| 2×3n |
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n |
| 1 |
| m |
| 1 |
| m2 |
| 1 |
| m3 |
| 1 |
| mn |
| 1 |
| m |
| 1 |
| m2 |
| 1 |
| m3 |
| 1 |
| mn |
| 5-1 |
| 5 |
| 52-1 |
| 52 |
| 53-1 |
| 53 |
| 5n-1 |
| 5n |
科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
数学问题：计算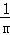
+
+
+…+
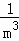（其中m，n都是正整数，且m≥2，n≥1）．
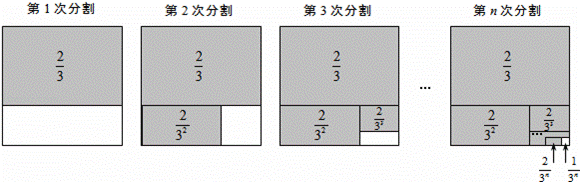
探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算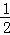
+
+
+…+
．
第1次分割，把正方形的面积二等分，其中阴影部分的面积为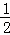
；
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为+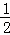
；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为++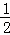
+…+
，最后空白部分的面积是．
根据第n次分割图可得等式：
+
+
+…+
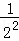=1﹣．
探究二：计算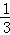
+
+
+…+
．
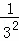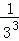第1次分割，把正方形的面积三等分，其中阴影部分的面积为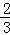
；
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为+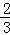
；
第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为++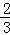
+…+
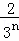，最后空白部分的面积是
．
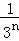根据第n次分割图可得等式：
+
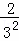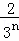++…+=1﹣，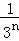
两边同除以2，得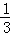
+
+
+…+
=
﹣
．
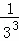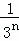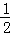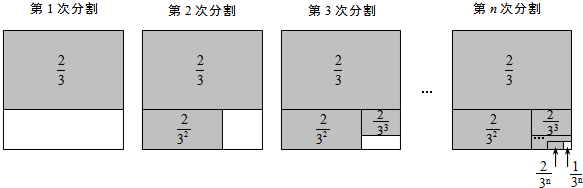
探究三：计算
+
+
+…+
．
（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算
+
+
+…+
．
（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式：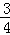 
+
+
+…+
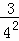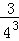=1﹣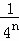
，
所以，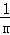
+
+
+…+
= 
﹣
．
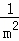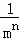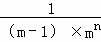拓广应用：计算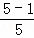 
+
+
+…+
．
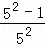科目：czsx 来源：2015-2016学年江苏省阜宁县八年级上学期期中统考数学试卷（解析版） 题型：填空题
数学实验室：
实验材料：硬纸板、剪刀、三角板
实验方法：剪裁、拼图、探索
实验目的：验证勾股定理，拼图填空：
操作：剪裁出若干个全等的直角三角形，三边长分别记为a、b、c，如图①。
（1）拼图一：分别用4张直角三角形纸片，拼成如图②、图③的形状，观察图②、图③可发现，图②中两个小正方形的面积之和 图③中小正方形的面积，（填“大于”“小于”“等于”）用关系式可表示为
（2）拼图二：用4张直角三角形纸片拼成如图④的形状，观察图形可以发现，图中共有3个正方形，它们的面积按大小顺序分别记为
，其关系是 ，用a、b、c可表示为 。
（3）拼图三：用8张直角三角形纸片拼成如图⑤的形状，图中3个正方形的面积按大小顺序分别记为，其关系是 ，用a、b、c可表示为 。
在区间[0，2π]内的零点，二分区间[0，2π]的次数为