10￡?à?ê|3?ê?á?D?oú°?é?μ?ìaoó(è?答案解析

科目：czsx 来源： 题型：

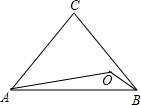
如图，△ABC中，AC=BC=5，∠ACB=80°，O为△ABC内一点，∠OAB=10°，∠OBA=30°，则线段AO的长是多少？

科目：czsx 来源： 题型：

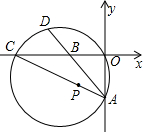
如图，在直角坐标系内，点B、C在x轴的负半轴上，点A在y轴的负半轴上．以AC为直径的圆与AB的延长线交于点D，弧CD=弧AO，如果AB=10，AO＞BO，且AO、BO是x的二次方程x²+kx+48=0的两个根．
（1）求点D的坐标；
（2）若点P在直径AC上，且AP=

1

4

AC，判断点（-2，-10）是否在过D、P两点的直线上，并说明理由．

科目：czsx 来源： 题型：

在直角坐标系中，有如图所示的Rt△ABO，AB⊥x轴于点B，斜边AO=10，sin∠AOB=

3

5

，反比例函数y=

k

x

(k＞0)的图象经过AO的中点C，且与AB交于点D．
（1）求此反比例函数的解析式；
（2）求点D的坐标．

科目：czsx 来源： 题型：

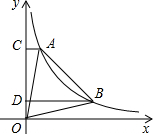
如图，点A和B是反比例函数y=

3

x

（x＞0）图象上任意两点，过A，B分别作y轴的垂线，垂足为C和D，连接AB，AO，BO，△ABO的面积为8，则梯形CABD的面积为（　　）

A、6

B、7

C、8

D、10

科目：czsx 来源： 题型：

29、附加题．
[友情提示]请同学们做完上面的考题后，再仔细认真检查一遍，估计一下你的得分情况．如果你感觉得分低于90分（及格线）请完成附加题．它可以帮助你及格，但总分不得超过90分．如果你卷面得分已达到90分或超过90分，则附加题得分不计入全卷总分．
（1）8的立方根是

2

．
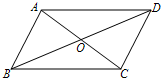
（2）如图，在▱ABCD中，AC、BD交于点O，若AO=5，则AC=

10

．

科目：czsx 来源： 题型：

16、如图，∠1=10°，AO⊥OC，点B、O、D在同一直线上，则∠2的度数为

100°

．

科目：czsx 来源： 题型：

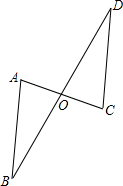
如图，线段AC、BD相交于点O，且AO=2，AC=5，BO=10，OD=15，求证：∠A=∠C．

科目：czsx 来源： 题型：

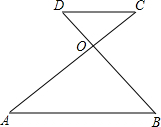
如图，AB∥CD，AC、BD交于O，BO=6，DO=3，AC=12，则AO长为（　　）

A．4

B．6

C．8

D．10

科目：czsx 来源： 题型：

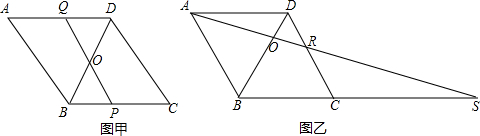
已知：在菱形ABCD中，O是对角线BD上的一动点．
（1）如图甲，P为线段BC上一点，连接PO并延长交AD于点Q，当O是BD的中点时，求证：OP=OQ；
（2）如图乙，连接AO并延长，与DC交于点R，与BC的延长线交于点S．若AD=4，∠DCB=60°，BS=10，求AS和OR的长．

科目：czsx 来源： 题型：

（2013•江东区模拟）如图，▱ABCD的对角线AC和BD相交于点O，AE垂直平分BC，分别交BD、BC于点F、E，已知sin∠BAE=

3

5

．
（1）求

AB

AD

的值；
（2）若AB=10，求AO和AF的值．

科目：czsx 来源： 题型：

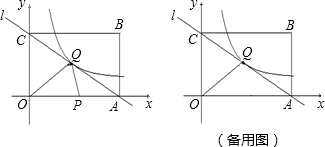
已知，矩形OABC在平面直角坐标系内的位置如图所示，点O为坐标原点，点A的坐标为（10，0），点B的坐标为（10，8）．
（1）直接写出点C的坐标为：C（

 

，

 

）；
（2）已知直线AC与双曲线y=

m

x

(m≠0)在第一象限内有一交点Q为（5，n）；
①求m及n的值；
②若动点P从A点出发，沿折线AO→OC的路径以每秒2个单位长度的速度运动，到达C处停止．求△OPQ的面积S与点P的运动时间t（秒）的函数关系式，并求当t取何值时S=10．

科目：czsx 来源： 题型：

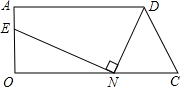
如图所示，梯形AOCD中，∠AOC=90°，AD=9，OC=10，AO=4在线段OC上任取一点N（不与O、C重合），连接DN，作NE⊥DN，与直线AO交于点E．
（1）当CN=2时，求OE；
（2）若CN=t，OE=s，求s关于自变量t的函数关系式；
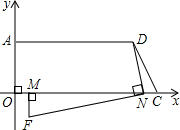
（3）探索与研究：如图2所示，分别以AO、OC所在的直线为y轴与x轴，O为原点，建立如图所示的直角坐标系，动点M从点O沿线段OC向C点运动，动点N从点C沿线段CO向点O同时等速运动，设现有一点F（x，y）满足MF⊥MN，NF⊥ND，试用含x的式子表示y．

科目：czsx 来源： 题型：

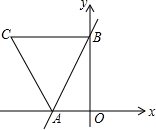
如图，已知一次函数y=2x+4的图象与x轴、y轴分别交于点A、B，且BC∥AO，梯形AOBC的面积为10．
（1）求点A、B、C的坐标；
（2）求直线AC的表达式．

科目：czsx 来源： 题型：

如图，在Rt△ABC中，∠C=90°，AC=10，BC=5，线段PQ=AB，P，Q两点分别在AC和过点A且垂直于AC的射线AO上运动，当AP=

5或10

5或10

时，△ABC和△PQA全等．

科目：czsx 来源： 题型：

（2008•上海）在△ABC中，AB=AC=5，cosB=

3

5

（如图）．如果圆O的半径为

10

，且经过点B，C，那么线段AO的长等于

3或5

3或5

．

科目：czsx 来源： 题型：

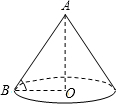
某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO=8米，母线AB=10米，则该圆锥的侧面积是

 

平方米（结果保留π）．

科目：czsx 来源： 题型：

如图所示，梯形AOCD中，AD=9，OC=10，AO=4，在线段OC上任取一点N（不与D，C重合），连接DN，作NE⊥DN，交AO于点E．

（1）当CN=2时，求点E的坐标．
（2）若CN=x，OE=y，求y与x的函数关系式．
（3）探索与研究：若点M从O点沿OC方向、N点从C点沿CO方向同时等速运动，现有一点F，满足MF⊥MN，NF⊥ND．
①猜想F点在什么线上运动？并求出这条线所对应的函数关系式，并写出自变量的取值范围；
②求出F点在运动过程中的最高点的坐标．

科目：czsx 来源： 题型：

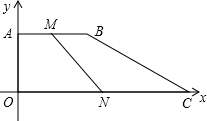
已知直角梯形OABC在如图所示的平面直角坐标系中，AB∥OC，AB=10，OC=22，BC=15，动点M从A点出发，以每秒一个单位长度的速度沿AB向点B运动，同时动点N从C点出发，以每秒2个单位长度的速度沿CO向O点运动．当其中一个动点运动到终点时，两个动点都停止运动．
（1）求B点坐标；
（2）设运动时间为t秒；
①当t为何值时，四边形OAMN的面积是梯形OABC面积的一半；
②当t为何值时，四边形OAMN的面积最小，并求出最小面积；
③若另有一动点P，在点M、N运动的同时，也从点A出发沿AO运动．在②的条件下，PM+PN的长度也刚好最小，求动点P的速度．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

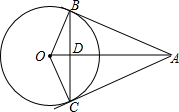
如图，AB、AC切⊙O于B、C，BC交OA于D，AB=10，AD=8，
（1）线段AO与BC有何关系？并说明理由；
（2）求BC的长．