练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >双曲线y2/12-x2/13=1 求y1+y3的值

    双曲线y2/12-x2/13=1 求y1+y3的值答案解析

    科目：gzsx 来源： 题型：

    如图，在双曲线-=1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.

    (1)求y1+y3的值；

    (2)证明线段AC的垂直平分线经过某一定点，并求此点坐标.

    查看答案和解析>>

    科目：gzsx 来源：数学教研室 题型：044

    在双曲线=－1的一支上有不同三点A(x1，y1)、B(x2，6)、C(x3，y3)与点F(0，5)的距离|AF|、|BF|、|CF|依次成等差数列。

    (1)求y1+y3的值；

    (2)求证线段AC的垂直平分线经过某一定点，并求出定点的坐标。　

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在双曲线=－1的一支上有不同的三点A(x1,y1),B(x2,6),C(x3,y3),与焦点F(0,5)的距离成等差数列.

    (1)求y1+y3的值;

    (2)求证:线段AC的垂直平分线经过某一定点,并求出定点坐标.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在双曲线=-1的上支上有不同的三点A(x1,y1)、B(x2,6)、C(x3,y3)，与焦点F(0，5)的距离成等差数列.

    (1)求y1+y3的值；

    (2)求证：线段AC的垂直平分线经过某一定点，并求出定点坐标.

    查看答案和解析>>

    科目：gzsx 来源： 题型：044

    在双曲线=－1的一支上有不同三点A(x1，y1)、B(x2，6)、C(x3，y3)与点F(0，5)的距离|AF|、|BF|、|CF|依次成等差数列。

    (1)求y1+y3的值；

    (2)求证线段AC的垂直平分线经过某一定点，并求出定点的坐标。　

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网如图，在双曲线
    y2
    12
    -
    x2
    13
    =1的上支上有三点A（x1，y1），B（x2，6），C（x3，y3），它们与点F（0，5）的距离成等差数列．
    （1）求y1+y3的值；
    （2）证明：线段AC的垂直平分线经过某一定点，并求此点坐标．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在双曲线的一支上有不同的三点A（x1,y1）、B（x2,6）、C(x3,y3),与焦点F（0，5）的距离成等差数列.

    （1）求y1+y3的值；

    （2）求证：线段AC的垂直平分线经过某一定点，并求出定点坐标.

    查看答案和解析>>

    科目：gzsx 来源： 题型：解答题

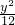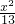    如图，在双曲线数学公式-数学公式=1的上支上有三点A（x1，y1），B（x2，6），C（x3，y3），它们与点F（0，5）的距离成等差数列．
    （1）求y1+y3的值；
    （2）证明：线段AC的垂直平分线经过某一定点，并求此点坐标．

    查看答案和解析>>

    科目：gzsx 来源：2006年高考第一轮复习数学：8.2 双曲线（解析版） 题型：解答题

    如图，在双曲线-=1的上支上有三点A（x1，y1），B（x2，6），C（x3，y3），它们与点F（0，5）的距离成等差数列．
    （1）求y1+y3的值；
    （2）证明：线段AC的垂直平分线经过某一定点，并求此点坐标．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)的定义域为［0,1］,且满足下列条件:

    ①对于任意x∈［0,1］,总有f(x)≥3,且f(1)=4;

    ②若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.

    (1)求f(0)的值;

    (2)求证:f(x)≤4;

    (3)当x∈(］(n=1,2,3,…)时,试证明f(x)＜3x+3.

    (文)如图,设抛物线y2=2px(p＞0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1)、(x2,y2),y1＞0,y2＜0,P是此抛物线的准线上的一点,O是坐标原点.

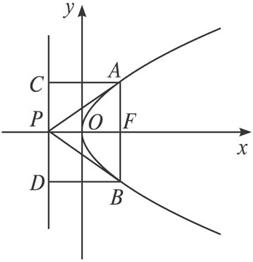
    (1)求证:y1y2=-p2;

    (2)直线PA、PF、PB的方向向量为(1,a)、(1,b)、(1,c),求证:实数a、b、c成等差数列;

    (3)若=0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （1）若不等式ax2+bx+2＞0的解集为(-
    1
    2
    ，
    1
    3
    )    ，求a+b的值；
    （2）若二次不等式ax2+bx+c＞0的解集是{x|
    1
    5
    ＜x＜
    1
    4
    }    ，求不等式2cx2-2bx-a＜0的解集．

    查看答案和解析>>

    科目：gzsx 来源：江苏省南通四县市合作编写的2007高考数学模拟试题集(二) 题型：013

    若双曲线y2－x2＝1与有唯一的公共点，则实数m的取值集合中元素的个数为

    [　　]

    A．2

    B．4

    C．5

    D．6

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若不等式ax2+bx+2＞0的解集为(-
    1
    2
    ，
    1
    3
    )    ，求a+b的值．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    若不等式ax2+bx+2＞0的解集为(-
    1
    2
    ，
    1
    3
    )    ，求a+b的值．

    查看答案和解析>>

    科目：gzsx 来源：2012高三数学一轮复习单元练习题函数的单调性 题型：044

    已知定义域为[0，1]的函数f(x)同时满足：

    ①对于任意的x∈[0，1]，总有f(x)≥0；

    ②f(1)＝1；

    ③若x1≥0，x2≥0，x1＋x2≤1，

    则有f(x1＋x2)≥f(x1)＋f(x2)．

    (1)求f(0)的值；

    (2)求f(x)的最大值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

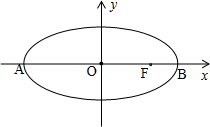    精英家教网在平面直角坐标系xoy中，如图，已知椭圆
    x2
    9
    +
    y2
    5
    =1    的左、右顶点为A、B，右焦点为F．设过点T（t，m）的直线TA、TB与椭圆分别交于点M（x1，y1）、N（x2，y2），其中m＞0，y1＞0，y2＜0．
    （1）设动点P满足PF2-PB2=4，求点P的轨迹；
    （2）设x1=2，x2=
    1
    3
    ，求点T的坐标；
    （3）设t=9，求证：直线MN必过x轴上的一定点（其坐标与m无关）．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设P（x0，y0）是抛物线y2=2px（p＞0）上异于顶点的定点，A（x1，y1），B（x2，y2）是抛物线上的两个动点，且直线PA与PB的倾斜角互补
    （1）求
    y1+y2y0
    的值
    （2）证明直线AB的斜率是非零常数．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知点P（x0，y0）（y0＞0）是抛物线y2=4x上一点，过点P作两条倾斜角互补的直线分别交抛物线于不同两点A（x1，y1），B（x2，y2）．
    （1）求
    y1+y2y0
    的值；
    （2）求证：直线AB的斜率为定值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知点F1，F2为双曲线C：x2-
    y2
    b2
    =1(b＞0)    的左、右焦点，过F2作垂直于x轴的直线，在x轴上方交双曲线于点M，且∠MF1F2=300，圆O的方程为x2+y2=b2．
    （1）求双曲线C的方程；
    （2）若双曲线C上的点到两条渐近线的距离分别为d1，d2，求d1•d2的值；
    （3）过圆O上任意一点P（x0，y0）作切线l交双曲线C于A，B两个不同点，求
    OA
    •
    OB
    的值．

    查看答案和解析>>

    科目：gzsx 来源：数学教研室 题型：044

    已知l1、l2是过点P（－，0）的两条互相垂直的直线，且l1、l2与双曲线y2－x2＝1各有两个交点，分别为A1、B1和A2、B2.

    （Ⅰ）求l1的斜率k1的取值范围；

    （Ⅱ）（理）若|A1B1|＝|A2B2|，求l1、l2的方程.

    （文）若A1恰是双曲线的一个顶点，求|A2B2|的值.

    查看答案和解析>>