
科目:gzsx 来源: 题型:
 设定义域为R的函数f(x)=
设定义域为R的函数f(x)=
|
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
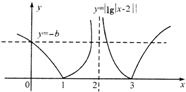 设定义域为R的函数f(x)=
设定义域为R的函数f(x)=
|
| A、4个 | B、5个 | C、7个 | D、8个 |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| 1+a |
| 2 |
| a |
| 1-3a |
| 1+a |
| 1-3a |
| 1+a |
科目:gzsx 来源: 题型:
|
| A、(0,1) | ||||
B、(0,
| ||||
| C、(1,2) | ||||
D、(1,
|
科目:gzsx 来源: 题型:
| 2x+1 | a+4x |
科目:gzsx 来源: 题型:
| 1 |
| n |
| 1 |
| n |
科目:gzsx 来源: 题型:
|
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
|
| A、b<0且c>0 |
| B、b>0且c<0 |
| C、b<0且c=0 |
| D、b≥0且c=0 |
科目:gzsx 来源: 题型:
|
科目:gzsx 来源: 题型:
| A、f(a)>f(0) | ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
科目:gzsx 来源: 题型:
|
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
科目:gzsx 来源: 题型:
| 1 | a |
科目:gzsx 来源: 题型:
| f(x1)-f(x2) |
| x1-x2 |
科目:gzsx 来源: 题型: