
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| AF1 |
| F1B |
| AF2 |
| F2C |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 5 |
| 8 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
科目:gzsx 来源: 题型:
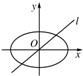 如图所示,设椭圆
如图所示,设椭圆| x2 |
| a2 |
| y2 |
| b2 |
A、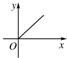 |
B、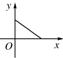 |
C、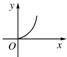 |
D、 |
科目:gzsx 来源: 题型:
 (2011•天津模拟)设椭圆
(2011•天津模拟)设椭圆| x2 |
| a2 |
| y2 |
| b2 |
| AF1 |
| AF2 |
| 27 |
| 7 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| AQ |
| 1 |
| e |
| 8 |
| 5 |
| 3 |
科目:gzsx 来源: 题型:
 如图,设椭圆
如图,设椭圆| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF1 |
| PF2 |
| 1 |
| 3 |
| ||
| 3 |
| ||
| 3 |
科目:gzsx 来源: 题型:
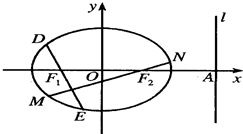 设椭圆
设椭圆| x2 |
| a2 |
| y2 |
| b2 |
| AF1 |
| AF2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
| 2 |
科目:gzsx 来源: 题型:
 (2014•兰州一模)设椭圆
(2014•兰州一模)设椭圆| x2 |
| a2 |
| y2 |
| b2 |
| AF1 |
| AF2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| A、圆x2+y2=3内 |
| B、圆x2+y2=3上 |
| C、圆x2+y2=3外 |
| D、以上三种都可能 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 3 |
| y2 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
科目:gzsx 来源: 题型:
 设椭圆
设椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
4
| ||
| 3 |
| AC |
| DB |
| AD |
| CB |