练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知抛物线y=x2一(k-1)x一3k一2

    已知抛物线y=x2一(k-1)x一3k一2答案解析

    科目：czsx 来源： 题型：

    3、已知抛物线y=x2-（k-1）x-3k-2与x轴交于A （α，0），B（β，0）两点，且α2+β2=17，则k=
    2
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知抛物线y=x2-（k-1）x-3k-2与x轴交于两点A（α，0），B（β，0），且α2+β2=17，求k的值．

    查看答案和解析>>

    科目：czsx 来源：新课标九年级数学竞赛培训第12讲：方程与函数（解析版） 题型：填空题

    已知抛物线y=x2-（k-1）x-3k-2与x轴交于A （α，0），B（β，0）两点，且α2+β2=17，则k=    ．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：填空题

    已知抛物线y=x2-（k-1）x-3k-2与x轴交于A （α，0），B（β，0）两点，且α2+β2=17，则k=______．

    查看答案和解析>>

    科目：czsx 来源： 题型：填空题

    已知抛物线y=x2-（k-1）x-3k-2与x轴交于A （α，0），B（β，0）两点，且α2+β2=17，则k=________．

    查看答案和解析>>

    科目：czsx 来源：期中题 题型：填空题

    已知抛物线y=x2-（k-l）x-3k-2与x轴交于A（α，0），B（β，0），且α2+β2=17，则k=（    ）。

    查看答案和解析>>

    科目：czsx 来源： 题型：

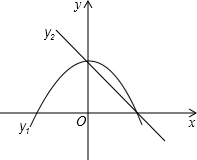    （2013•衡水二模）如图，已知抛物线y1=-x2+1，直线y2=-x+1，当x任取一值时，x对应的函数值分别为y1，y2，若y1≠y2，取y1，y2中的较小值记为M1，若y1=y2，记M=y1=y2，例如：x=2时，y1=-3，y2=-1，y1＜y2，M=-3．下列判断：
    ①当x＞0时，y1＞y2；
    ②当x＜0时，x值越大，M值越大；
    ③使得M大于1的x值不存在；
    ④使得M=0的x值是1．
    其中正确的是（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知抛物线y=x2+x+4．
    （1）求此抛物线对称轴与横轴交点A的坐标；
    （2）设原点为O，在抛物线上任取点P，求三角形OAP的面积的最小值；
    （3）若x为整数，在使得y为完全平方数的所有x的值中，设x的最大值为a，最小值为b，次小值为c．（注：一个数如果是另一个整数的完全平方，那么我们就称这个数为完全平方数．）求a、b、c的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

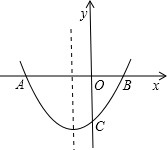    （2013•沙市区一模）如图，已知抛物线y=x2-（m2-2）x-2m与x轴交与点A（x1，0），B（x2，0），与y轴交与点C，且满足
    1
    x1
    +
    1
    x2
    =
    1
    2
    ．
    （1）求这条抛物线的解析式；
    （2）若点M是这条抛物线对称轴上的一个动点，当MB+MC的值最小时，求点M的坐标．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    小兰和小芳分别用掷A，B两枚骰子的方法来确定P（x，y）的位置，她们规定：小兰掷得的点数为x，小芳掷得的点数为y，那么，她们各掷一次所确定的点落在已知抛物线y=x2上的概率为（　　）
    A、
    6
    36
    B、
    1
    18
    C、
    1
    12
    D、
    1
    9

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2012•金湾区一模）已知抛物线y=x2+kx-
    3
    4
    k2（k为常数，且k＞0）．
    （1）证明：此抛物线与x轴总有两个不同的交点；
    （2）设抛物线与x轴交于M（x1，0），N（x2，0）两点，且
    1
    x1
    +
    1
    x2
    =
    2
    3
    ，求k的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•嘉定区一模）已知抛物线y=-x2+bx+c如图所示，那么b、c的取值范围是（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•黄埔区一模）已知抛物线y=x2+（m+4）x-2（m+6）（m为常数，m≠-8））与x轴有两个不同的交点A、B，点A、点B关于直线x=1对称，抛物线的顶点为C．
    （1）并此抛物线的解析式；
    （2）求点A、B、C的坐标．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•滨湖区一模）已知抛物线y=x2-2ax+a2 （a为常数，a＞0），G为该抛物线的顶点．
    （1）如图1，当a=2时，抛物线与y轴交于点M，求△GOM的面积；
    （2）如图2，将抛物线绕顶点G逆时针旋转90°，所得新图象与y轴交于A、B两点（点A在点B的上方），D为x轴的正半轴上一点，以OD为一对角线作平行四边形OQDE，其中Q点在第一象限．QE交OD于点C，若QO平分∠AQC，AQ=2QC．
    ①求证：△AQO≌△EQO；
    ②若QD=OG，试求a的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1、2、3、4、5、6）．用小明掷A立方体朝上的数字为x，小明掷B立方体朝上的数字为y来确定点P（x，y），则小明各掷一次所确定的点P落在已知抛物线y=x2-4x+5上的概率是
     
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    24、已知抛物线y=x2+4x+m（m为常数）经过点（0，4）
    （1）求m的值；
    （2）将该抛物线先向右、再向下平移得到另一条抛物线．已知这条平移后的抛物线满足下述两个条件：它的对称轴（设为直线l2）与平移前的抛物线的对称轴（设为l1）关于y轴对称；它所对应的函数的最小值为-8，试求平移后的抛物线所对应的函数关系式．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知抛物线y=x2+bx+c与直线y=x+1有两个交点A、B．
    （1）当AB的中点落在y轴时，求c的取值范围；
    （2）当AB=2
    		2
    ，求c的最小值，并写出c取最小值时抛物线的解析式；
    （3）设点P（t，T）在AB之间的一段抛物线上运动，S（t）表示△PAB的面积．
    ①当AB=2
    		2
    ，且抛物线与直线的一个交点在y轴时，求S（t）的最大值，以及此时点P的坐标；
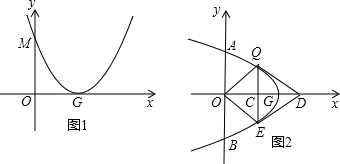
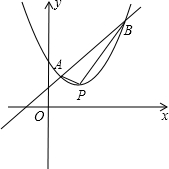    ②当AB=m（正常数）时，S（t）是否仍有最大值，若存在，求出S（t）的最大值以及此时精英家教网点P的坐标（t，T）满足的关系，若不存在说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    现有A、B两枚均匀的小立方体，立方体的每个面上分别标有数字1，2，3，4，5，6．用小莉掷A立方体朝上的数字为x，小明掷B立方体朝上的数字为y来确定点P（x，y），那么它们各掷一次所确定的点P落在已知抛物线y=-x2+4x上的概率为
    1
    12
    1
    12
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2012•大丰市一模）已知抛物线y=x2+x-1经过点P（m，5），则代数式m2+m+2006的值为（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知抛物线y=x2-4x+1，将此抛物线沿x轴方向向左平移4个单位长度，得到一条新的抛物线．
    （1）求平移后的抛物线解析式；
    （2）由抛物线对称轴知识我们已经知道：直线x=m，即为过点（m，0）平行于y轴的直线，类似地，直线y=m，即为过点（0，m）平行于x轴的直线、请结合图象回答：当直线y=m与这两条抛物线有且只有四个交点，实数m的取值范围；
    （3）若将已知的抛物线解析式改为y=x2+bx+c（b＜0），并将此抛物线沿x轴向左平移-b个单位长度，试回答（2）中的问题．精英家教网

    查看答案和解析>>