
科目:gzsx 来源:2011-2012学年江苏省扬州市宝应县安宜高级中学高一(上)期中数学试卷(解析版) 题型:填空题
科目:gzsx 来源:2010年广东省肇庆市高考数学二模试卷(文科)(解析版) 题型:选择题
 =1-bi(a,b是实数,i是虚数单位),则a+b=( )
=1-bi(a,b是实数,i是虚数单位),则a+b=( )科目:gzsx 来源: 题型:
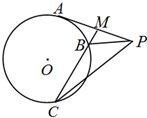 选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,
选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,
|
|
|
|
| π |
| 4 |
| 2 |
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
科目:gzsx 来源: 题型:
| A |
| B |
| 2 |
| a |
| 1 |
| 3b |
科目:gzsx 来源: 题型:
| OA |
| a |
| OB |
| b |
| a |
| 2 |
| b |
| 3 |
| a |
| b |
| APn |
| b |
| a |
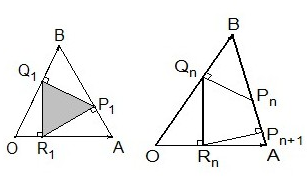
| AB |
| BQ1 |
| 2 |
| 3 |
| b |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
科目:gzsx 来源: 题型:
| f(x) |
| g(x) |
| A、F(sinα)<F(cosβ) |
| B、F(sinα)<F(sinβ) |
| C、F(cosα)>F(cosβ) |
| D、F(cosα)<F(cosβ) |
科目:gzsx 来源: 题型: