练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >其中p为函数图象的最高点，A,B

    其中p为函数图象的最高点，A,B答案解析

    科目：gzsx 来源： 题型：

    已知函数f（x）=Asin（
    π
    6
    x+ϕ    ）（A＞0，0＜ϕ＜
    π
    2
    ）的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为（2，A），点R的坐标为（2，0）．若∠PRQ=
    2π
    3
    ，则y=f（x） 的最大值及ϕ的值分别是（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在下列命题中：
    （1）若“p且q”为假命题，则p，q均为假命题；
    （2）(1+
    3x
    )6(1+
    1
    4x
    )10    展开式中的常数项为4246；
    （3）如果不等式
    		4x-x2
    ＞（a-1）x的解集为A，且A⊆{x|0＜x＜2}，那么实数a的取值范围是a∈（2，+∞）．
    （4）函数f(x)=
    1
    3
    x3+
    1
    2
    ax2+
    a2-8
    4
    x    在x=1处的切线恰好在此处穿过函数图象的充要条件是a=-2
    其中真命题的序号是
     
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2011•成都模拟）对函数Φ（x），定义fk（x）=Φ（x-mk）+nk（其中x∈（mk，m+mk]，k∈Z，m＞0，n＞0，且m、n为常数）为Φ（x）的第k阶阶梯函数，m叫做阶宽，n叫做阶高，已知阶宽为2，阶高为3．
    （1）当Φ（x）=2x时
    ①求f0（x）和fk（x）的解析式；
    ②求证：Φ（x）的各阶阶梯函数图象的最高点共线；
    （2）若Φ（x）=x2，则是否存在正整数k，使得不等式fk（x）＜（1-3k）x+4k2+3k-1有解？若存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网已知函数f（x）=2Acos2（
    π
    6
    x+φ）-A（X∈R，A＞0，|φ|＜
    π
    2
    ），y=f（x）的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为（1，A）
    （1）求f（x）的最小正周期及φ的值；
    （2）若点R的坐标为（1，0），∠PRQ=
    2π
    3
    ，求△PRQ的面积．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    对函数Φ（x），定义fk（x）=Φ（x-mk）+nk（其中x∈（mk，m+mk]，k∈Z，m＞0，n＞0，且m、n为常数）为Φ（x）的第k阶阶梯函数，m叫做阶宽，n叫做阶高，当阶宽为2，阶高为3时，若Φ（x）=2x．
    （1）求f0（x）和fk（x）的解析式；
    （2）求证：Φ（x）的各阶阶梯函数图象的最高点共线．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

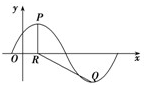    精英家教网已知函数f(x)=Asin (
    π
    3
    x+φ)    ，x∈R，A＞0，0＜φ＜
    π
    2
    ．y=f（x）的部分图象，如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为（1，A）．
    （Ⅰ）求f（x）的最小正周期及φ的值；
    （Ⅱ）若点R的坐标为（1，0），∠PRQ=
    2π
    3
    ，求A的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

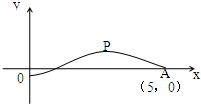    如图，是函数y=Asin（ωx+φ），（-π＜φ＜π）的图象的一段，O是坐标原点，P是图象的最高点，A点坐标为（5，0），若|
    OP
    |=
    		10
    ，
    OP
    •
    OA
    =15    ，则此函数的解析式为
    y=sin(
    π
    4
    x-
    π
    4
    )
    y=sin(
    π
    4
    x-
    π
    4
    )
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网函数y=sinπx的部分图象如图所示，O为坐标原点，P是图象的最高点，A、B分别是图象与x轴的两交点，则tan∠APB等于（　　）

    查看答案和解析>>

    科目：gzsx 来源：2011年四川省成都市毕业班摸底测试（文科）数学卷 题型：解答题

    （本小题满分14分） 对函数Φ（x），定义fk（x）＝Φ（x－mk）＋nk（其中x∈（mk，

    m＋mk]，k∈Z，m＞0，n＞0，且m、n为常数）为Φ（x）的第k阶阶梯函数，m叫做阶宽，n叫做阶高，已知阶宽为2，阶高为3．

       （1）当Φ（x）＝2x时  ①求f0（x）和fk（x）的解析式；  ②求证：Φ（x）的各阶阶梯函数图象的最高点共线；

      

     

    查看答案和解析>>

    科目：gzsx 来源：2010-2011学年四川省成都市高三摸底数学试卷（文科）（解析版） 题型：解答题

    对函数Φ（x），定义fk（x）=Φ（x-mk）+nk（其中x∈（mk，m+mk]，k∈Z，m＞0，n＞0，且m、n为常数）为Φ（x）的第k阶阶梯函数，m叫做阶宽，n叫做阶高，当阶宽为2，阶高为3时，若Φ（x）=2x．
    （1）求f（x）和fk（x）的解析式；
    （2）求证：Φ（x）的各阶阶梯函数图象的最高点共线．

    查看答案和解析>>

    科目：gzsx 来源：2011年四川省成都市高三摸底测试数学试卷（文科）（解析版） 题型：解答题

    对函数Φ（x），定义fk（x）=Φ（x-mk）+nk（其中x∈（mk，m+mk]，k∈Z，m＞0，n＞0，且m、n为常数）为Φ（x）的第k阶阶梯函数，m叫做阶宽，n叫做阶高，当阶宽为2，阶高为3时，若Φ（x）=2x．
    （1）求f（x）和fk（x）的解析式；
    （2）求证：Φ（x）的各阶阶梯函数图象的最高点共线．

    查看答案和解析>>

    科目：gzsx 来源：2012-2013学年江西省宜春市五校高三（上）12月月考数学试卷（文科）（解析版） 题型：填空题

    如图，是函数y=Asin（ωx+φ），（-π＜φ＜π）的图象的一段，O是坐标原点，P是图象的最高点，A点坐标为（5，0），若，则此函数的解析式为    ．

    查看答案和解析>>

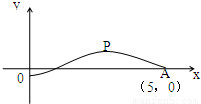
    科目：gzsx 来源：2011-2012学年福建省厦门市高三（上）期末数学试卷（文科）（解析版） 题型：选择题

    已知函数f（x）=Asin（）（A＞0，0＜ϕ＜）的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为（2，A），点R的坐标为（2，0）．若∠PRQ=，则y=f（x） 的最大值及ϕ的值分别是（ ）

    A．2，
    B．，
    C．，
    D．2，

    查看答案和解析>>

    科目：gzsx 来源：2011年四川省成都市高三摸底测试数学试卷（理科）（解析版） 题型：解答题

    对函数Φ（x），定义fk（x）=Φ（x-mk）+nk（其中x∈（mk，m+mk]，k∈Z，m＞0，n＞0，且m、n为常数）为Φ（x）的第k阶阶梯函数，m叫做阶宽，n叫做阶高，已知阶宽为2，阶高为3．
    （1）当Φ（x）=2x时
    ①求f（x）和fk（x）的解析式；
    ②求证：Φ（x）的各阶阶梯函数图象的最高点共线；
    （2）若Φ（x）=x2，则是否存在正整数k，使得不等式fk（x）＜（1-3k）x+4k2+3k-1有解？若存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源：2012-2013学年江西省宜春市五校高三（上）联考数学试卷（文科）（解析版） 题型：填空题

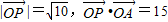    如图，是函数y=Asin（ωx+φ），（-π＜φ＜π）的图象的一段，O是坐标原点，P是图象的最高点，A点坐标为（5，0），若，则此函数的解析式为    ．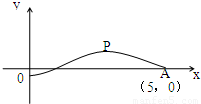

    查看答案和解析>>

    科目：gzsx 来源：2010-2011学年四川省成都市高三摸底数学试卷（理科）（解析版） 题型：解答题

    对函数Φ（x），定义fk（x）=Φ（x-mk）+nk（其中x∈（mk，m+mk]，k∈Z，m＞0，n＞0，且m、n为常数）为Φ（x）的第k阶阶梯函数，m叫做阶宽，n叫做阶高，已知阶宽为2，阶高为3．
    （1）当Φ（x）=2x时
    ①求f（x）和fk（x）的解析式；
    ②求证：Φ（x）的各阶阶梯函数图象的最高点共线；
    （2）若Φ（x）=x2，则是否存在正整数k，使得不等式fk（x）＜（1-3k）x+4k2+3k-1有解？若存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源：2010年内蒙古元宝山区高三第一次摸底考试理科数学卷 题型：解答题

    （本小题满分14分） 对函数Φ（x），定义fk（x）＝Φ（x－mk）＋nk（其中x∈（mk，

    m＋mk]，k∈Z，m＞0，n＞0，且m、n为常数）为Φ（x）的第k阶阶梯函数，m叫做阶宽，n叫做阶高，已知阶宽为2，阶高为3．

    （1）当Φ（x）＝2x时  ①求f0（x）和fk（x）的解析式；  ②求证：Φ（x）的各阶阶梯函数图象的最高点共线；

    （2）若Φ（x）＝x2，则是否存在正整数k，使得不等式fk（x）＜（1－3k）x＋4k2＋3k－1有解？若存在，求出k的值；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：gzsx 来源：2012-2013学年湖南省永州市祁阳四中高三（上）段考数学试卷（文科）（解析版） 题型：解答题

    已知函数，x∈R，A＞0，．y=f（x）的部分图象，如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为（1，A）．
    （Ⅰ）求f（x）的最小正周期及φ的值；
    （Ⅱ）若点R的坐标为（1，0），，求A的值．

    查看答案和解析>>

    科目：gzsx 来源：内蒙古元宝山区一中2011届高三第一次摸底考试文科数学试题 题型：044

    对函数Φ(x)，定义fk(x)＝Φ(x－mk)＋nk(其中x∈(mk，m＋mk]，k∈Z，m＞0，n＞0，且m、n为常数)为Φ(x)的第k阶阶梯函数，m叫做阶宽，n叫做阶高，已知阶宽为2，阶高为3．

    (1)当Φ(x)＝2x时

    ①求f0(x)和fk(x)的解析式；

    ②求证：Φ(x)的各阶阶梯函数图象的最高点共线；

    (2)若Φ(x)＝x2，则是否存在正整数k，使得不等式fk(x)＜(1－3k)x＋4k2＋3k－1有解？若存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源：河北省冀州中学2012届高三上学期期中考试数学文科试题(A) 题型：044

    已知函数f(x)＝Asin(x＋)，x∈R，A＞0，0＜＜．y＝f(x)的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为(1，A)．

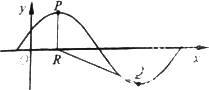
    (Ⅰ)求f(x)的最小正周期及的值；

    (Ⅱ)若点R的坐标为(1，0)，∠PRQ＝，求A的值．

    查看答案和解析>>