科目：czsx 来源： 题型：
（2012•攀枝花）如图，以BC为直径的⊙O1与⊙O2外切，⊙O1与⊙O2的外公切线交于点D，且∠ADC=60°，过B点的⊙O1的切线交其中一条外公切线于点A．若⊙O2的面积为π，则四边形ABCD的面积是| 3 |
| 3 |
科目：czsx 来源： 题型：
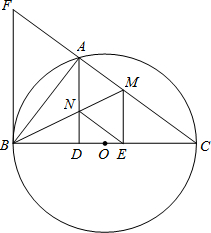⊥BC于点E，AB2=AF•AC，cos∠ABD=| 3 | 5 |
科目：czsx 来源： 题型：
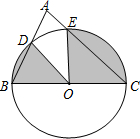
（2013•眉山）如图，以BC为直径的⊙O与△ABC的另两边分别相交于点D、E．若∠A=60°，BC=4，则图中阴影部分的面积为| 4 |
| 3 |
| 4 |
| 3 |
科目：czsx 来源： 题型：
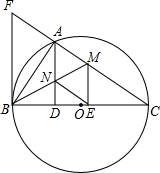
（2012•浦口区一模）如图，以BC为直径的⊙O与△ABC的另两边分别相交于点D、E．若∠A=70°，BC=2，则图中阴影部分面积为| 7 |
| 18 |
| 7 |
| 18 |
科目：czsx 来源： 题型：
如图，以BC为直径的⊙O交△CFB的边CF于点A，BM平分∠ABC交AC于点M，AD⊥BC于点D，AD交BM于点N，ME⊥BC于点E，AB2=AF•AC，cos∠ABD=| 3 | 5 |
科目：czsx 来源：2012年初中毕业升学考试（四川攀枝花卷）数学（解析版） 题型：填空题
如图，以BC为直径的⊙O1与⊙O2外切，⊙O1与⊙O2的外公切线交于点D，且∠ADC=60°，过B点的⊙O1的切线交其中一条外公切线于点A．若⊙O2的面积为π，则四边形ABCD的面积是 ．
科目：czsx 来源：2012届河南驻马店中考二模数学试卷（带解析） 题型：解答题
如图，以BC为直径的圆0交∆CFB的边CF于点A，BM平分∠ABC交AC于点M,AD⊥BC于点D，AD交BM于点N,ME⊥BC于点E，AB2 =AF．AC.
【小题1】求△ANM≅△ENM;
【小题2】求证：FB是圆O的切线
【小题3】证明四边形AMEN是菱形．
科目：czsx 来源：2011-2012学年河南驻马店中考二模数学试卷（解析版） 题型：解答题
如图，以BC为直径的圆0交∆CFB的边CF于点A，BM平分∠ABC交AC于点M,AD⊥BC于点D，AD交BM于点N,ME⊥BC于点E，AB2 =AF．AC.
1.求△ANM≅△ENM;
2.求证：FB是圆O的切线
3.证明四边形AMEN是菱形．
科目：czsx 来源：2013年初中毕业升学考试（四川眉山卷）数学（解析版） 题型：填空题
（2013年四川眉山3分）如图，以BC为直径的⊙O与△ABC的另两边分别相交于点D、E．若∠A=60°，BC=4，则图中阴影部分的面积为 ．（结果保留π）
科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
如图，以BC为直径的圆0交∆CFB的边CF于点A，BM平分∠ABC交AC于点M,AD⊥BC于点D，AD交BM于点N,ME⊥BC于点E，AB2 =AF．AC.
1.求△ANM≅△ENM;
2.求证：FB是圆O的切线
3.证明四边形AMEN是菱形．
科目：czsx 来源：2012年四川省乐山市井研县石牛乡九年级数学联考试卷（3月份）（解析版） 题型：解答题
，AD=12．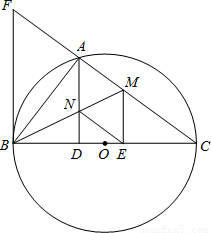
科目：czsx 来源：2012年江苏省扬州中学树人学校中考数学二模试卷（解析版） 题型：填空题
科目：czsx 来源：第24章《圆》常考题集（05）：24.1 圆（解析版） 题型：选择题
科目：czsx 来源： 题型：解答题
如图，以BC为直径的⊙O交△CFB的边CF于点A，BM平分∠ABC交AC于点M，AD⊥BC于点D，AD交BM于点N，ME⊥BC于点E，AB2=AF•AC，cos∠ABD=
，AD=12．科目：czsx 来源：2012年10月中考数学模拟试卷（4）（解析版） 题型：填空题
科目：czsx 来源：第3章《圆》中考题集（44）：3.2 点、直线与圆的位置关系，圆的切线（解析版） 题型：解答题
，AD=12．
科目：czsx 来源：2010年湖北省天门中学优录考试数学试卷（解析版） 题型：解答题
，AD=12．
11、如图，以BC为直径的半圆中，点A、D在半圆周上且AD=DC，若∠ABC=30°，则∠ADC的度数为（ ）
（2013•澄海区模拟）如图，以BC为直径的⊙O与△ABC的另两边分别相交于点D、E．若∠A=60°，BC=2，则图中阴影部分的面积为