精英家教网 >
试题搜索列表 >定义在R上的函数f(x)满足f(1)=1,且对任意x∈R,都有f′(x)< 1 2 ,则不等式f(x2)> x2+1 2 %
定义在R上的函数f(x)满足f(1)=1,且对任意x∈R,都有f′(x)< 1 2 ,则不等式f(x2)> x2+1 2 %答案解析
科目:gzsx
来源:
题型:
对于定义在D上的函数y=f(x),若同时满足.
①存在闭区间[a,b]⊆D,使得任取x
1∈[a,b],都有f(x
1)=c (c是常数);
②对于D内任意x
2,当x
2∉[a,b]时总有f(x
2)>c称f(x)为“平底型”函数.
(1)(理)判断f
1(x)=|x-1|+|x-2|,f
2(x)=x+|x-2|是否是“平底型”函数?简要说明理由;
(文)判断f
1(x)=|x-1|+|x-2|,f
2(x)=x-|x-3|是否是“平底型”函数?简要说明理由;
(2)(理)设f(x)是(1)中的“平底型”函数,若|t-k|+|t+k|≥|k|•f(x),k∈R且k≠0,对一切t∈R恒成立,求实数x的范围;
(文)设f(x)是(1)中的“平底型”函数,若|t-1|+|t+1|≥f(x),对一切t∈R恒成立,求实数x的范围;
(3)(理)若F(x)=mx+
,x∈[-2,+∞)是“平底型”函数,求m和n的值;
(文)若F(x)=m|x-1|+n|x-2|是“平底型”函数,求m和n满足的条件.
查看答案和解析>>
科目:gzsx
来源:2009-2010学年上海市十一校高三联考数学试卷(解析版)
题型:解答题
对于定义在D上的函数y=f(x),若同时满足.
①存在闭区间[a,b]⊆D,使得任取x
1∈[a,b],都有f(x
1)=c (c是常数);
②对于D内任意x
2,当x
2∉[a,b]时总有f(x
2)>c称f(x)为“平底型”函数.
(1)(理)判断f
1(x)=|x-1|+|x-2|,f
2(x)=x+|x-2|是否是“平底型”函数?简要说明理由;
(文)判断f
1(x)=|x-1|+|x-2|,f
2(x)=x-|x-3|是否是“平底型”函数?简要说明理由;
(2)(理)设f(x)是(1)中的“平底型”函数,若|t-k|+|t+k|≥|k|•f(x),k∈R且k≠0,对一切t∈R恒成立,求实数x的范围;
(文)设f(x)是(1)中的“平底型”函数,若|t-1|+|t+1|≥f(x),对一切t∈R恒成立,求实数x的范围;
(3)(理)若F(x)=mx+
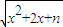
,x∈[-2,+∞)是“平底型”函数,求m和n的值;
(文)若F(x)=m|x-1|+n|x-2|是“平底型”函数,求m和n满足的条件.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
对于定义在D上的函数y=f(x),若同时满足.
①存在闭区间[a,b]⊆D,使得任取x1∈[a,b],都有f(x1)=c (c是常数);
②对于D内任意x2,当x2∉[a,b]时总有f(x2)>c称f(x)为“平底型”函数.
(1)(理)判断f1(x)=|x-1|+|x-2|,f2(x)=x+|x-2|是否是“平底型”函数?简要说明理由;
(文)判断f1(x)=|x-1|+|x-2|,f2(x)=x-|x-3|是否是“平底型”函数?简要说明理由;
(2)(理)设f(x)是(1)中的“平底型”函数,若|t-k|+|t+k|≥|k|•f(x),k∈R且k≠0,对一切t∈R恒成立,求实数x的范围;
(文)设f(x)是(1)中的“平底型”函数,若|t-1|+|t+1|≥f(x),对一切t∈R恒成立,求实数x的范围;
(3)(理)若F(x)=mx+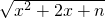 ,x∈[-2,+∞)是“平底型”函数,求m和n的值;
,x∈[-2,+∞)是“平底型”函数,求m和n的值;
(文)若F(x)=m|x-1|+n|x-2|是“平底型”函数,求m和n满足的条件.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在R上的函数f(x)满足:如果对任意x
1,x
2∈R,都有
f()≤[f(x1)+f(x2)],则称f(x)是R上凹函数.已知二次函数f(x)=ax
2+x(a∈R,且a≠0).
(1)求证:当a>0时,函数f(x)的凹函数;
(2)如果x∈[0,1]时,|f(x)|≤1,试求a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知定义在R上的函数f(x),对任意的实数m、n,都有f(m+n)=f(m)f(n)成立,且当x>0时,有f(x)>1成立.
(Ⅰ)求f(0)的值,并证明当x<0时,有0<f(x)<1成立;
(Ⅱ)判断函数f(x)在R上的单调性,并证明你的结论;
(Ⅲ)若f(1)=2,数列{a
n}满足a
n=f(n)(n∈N
*),记
Sn=++…+,且对一切正整数n有
f()>2Sn恒成立,求实数m的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在R上的函数f(x)满足:对任意a,b∈R都有f(a+b)=f(a)•f(b),且f(1)=3.
(1)求f(0),f(-1)的值;
(2)若当x>0时,有f(x)>1,判断函数f(x)的单调性,并说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在R上的函数y=f(x)满足:对任意的x,y∈R都有
f(x)+f(y)=f()成立,f(1)=1,且当x>0时,f(x)>0.
(1)求f(-1)的值,并判断y=f(x)的奇偶性;
(2)证明:y=f(x)在(0,+∞)上的单调递增;
(3)若关于x的方程
2f(x)=f()在(2,+∞)上有两个不同的实根,求实数a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知定义在R上的函数f(x)对任意实数x,y都满足f(x+y)=f(x)+f(y),且当x>0时,f(x)>0
(1)判断函数f(x)的奇偶性,并证明
(2)解不等式f(a-4)+f(2a+1)<0.
查看答案和解析>>
科目:gzsx
来源:
题型:
(A类)定义在R上的函数y=f(x),对任意的a,b∈R,满足f(a+b)=f(a)•f(b),当x>0时,有f(x)>1,其中f(1)=2
(1)求f(0)、f(-1)的值; (2)证明y=f(x)在(0,+∞)上是增函数;(3)求不等式f(x+1)<4的解集.
(B类)已知定义在R上的奇函数
f(x)= .
(1)求a,b的值;
(2)若不等式
-m2+(k+2)m-<f(x)<m2+2km+k+对一切实数x及m恒成立,求实数k的取值范围;
(3)定义:若存在一个非零常数T,使得f(x+T)=f(x)对定义域中的任何实数x都恒成立,那么,我们把f(x)叫以T为周期的周期函数,它特别有性质:对定义域中的任意x,f(x+nT)=f(x),(n∈Z).若函数g(x0是定义在R上的周期为2的奇函数,且当x∈(-1,1)时,g(x)=f(x)-x,求方程g(x)=0的所有解.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•梅州二模)定义在R上的函数f(x)满足:f(x+y)=f(x)f(y),且当x>0时,f(x)>1.数列{a
n}满足a
n=1-3k,f(a
n+1)=
.
(1)求f(0)的值,并证明f(x)是定义域上的增函数:
(2)求数列{a
n}的通项公式;
(3)设0<a<b
nS
n为数列{a
n}的前n项和,是否存在实数k,使得对任意正整数n,都有a<S
n<b?若存在,求出k的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知f(x),g(x)都是定义在R上的函数,对任意x、y满足f(x-y)=f(x)•g(y)-g(x)•f(y),且f(-2)=f(1)≠0,则g(1)+g(-1)=( )
查看答案和解析>>
科目:gzsx
来源:
题型:
已知定义在R上的函数f(x)=x2+ax+b其函数图象经过原点,且对任意的实数x都有f(1+x)=f(1-x)成立.
(Ⅰ)求实数 a,b的值;
(Ⅱ)若函数g(x)是定义在R上的奇函数,且满足当x≥0时,g(x)=f(x),则求g(x)的解析式.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在R上的单调函数f(x)满足f(3)=log23且对任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求证f(x)为奇函数;
(2)若f(k•3x)+f(3x-9x-2)<0对任意x∈R恒成立,求实数k的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在R上的单调函数f(x)满足f(3)=log23且对任意x,y∈R都有f(x+y)=f(x)+f(y),若f(k•3x)+f(3x-9x-2)<0对任意x∈R恒成立,则实数k的取值范围为( )
| A、(-1,-1+2) |
| B、(-∞,-1+2) |
| C、(-∞,-1) |
| D、[-1+2,+∞) |
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在R上的函数y=f(x)是减函数,且对任意的a∈R,都有f(-a)+f(a)=0,若x,y满足不等式f(x2-2x)+f(2y-y2)≤0,则当1≤x≤4时,2x-y的最大值为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在R上的函数f(x)满足f(1)=1,且对任意x∈R都有f′(x)
<,则不等式f(x
2)>
的解集为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
给出下列四个命题:
①如果复数z满足|z+i|+|z-i|=2,则复数z在复平面上所对应点的轨迹是椭圆.
②设f(x)是定义在R上的函数,且对任意的x∈R,|f(x)|=|f(-x)|恒成立,则f(x)是R上的奇函数或偶函数.
③已知曲线
C:-=1和两定点E(-5,0)、F(5,0),若P(x,y)是C上的动点,则||PE|-|PF||<6.
④设定义在R上的两个函数f(x)、g(x)都有最小值,且对任意的x∈R,命题“f(x)>0或g(x)>0”正确,则f(x)的最小值为正数或g(x)的最小值为正数.
上述命题中错误的个数是( )
查看答案和解析>>
科目:gzsx
来源:
题型:
对于无穷数列{x
n}和函数f(x),若x
n+1=f(x
n)(n∈N
+),则称f(x)是数列{x
n}的母函数.
(Ⅰ)定义在R上的函数g(x)满足:对任意α,β∈R,都有g(αβ)=αg(β)+βg(α),且
g()=1;又数列{a
n}满足:
an=g().
求证:(1)f(x)=x+2是数列{2
na
n}的母函数;
(2)求数列{a
n}的前项n和S
n.
(Ⅱ)已知
f(x)=是数列{b
n}的母函数,且b
1=2.若数列
{}的前n项和为T
n,求证:
25(1-0.99n)<Tn<250(1-0.999n)(n≥2).
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在R上的函数f(x)满足:对任意实数m,n,总有f(m+n)=f(m)•f(n),且当x>0时,0<f(x)<1.
(1)试求f(0)的值;
(2)判断f(x)的单调性并证明你的结论;
(3)若对任意x∈[1,4]时,不等式f(x2+2)<f(ax)都成立,求a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y∈R,有f(x+y)=f(x)•f(y),且f(1)=2
(1)求f(0)的值;
(2)求证:对任意的x∈R,都有f(x)>0
(3)解不等式f(3-x2)>4.
查看答案和解析>>

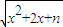 ,x∈[-2,+∞)是“平底型”函数,求m和n的值;
,x∈[-2,+∞)是“平底型”函数,求m和n的值;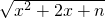 ,x∈[-2,+∞)是“平底型”函数,求m和n的值;
,x∈[-2,+∞)是“平底型”函数,求m和n的值;