数列an的前n相和为Sn,已知a1=a,an+1=Sn+3n答案解析
科目:gzsx
来源:
题型:
(2010•昆明模拟)设等差数列{an}的前n和为Sn,等比数列{bn}的前n和为Tn,已知a1=1,b1=1,a2b2=1,S3T3=13,求{an},{bn}的通项公式.
查看答案和解析>>
科目:gzsx
来源:2009-2010学年云南省昆明市高三质量检测数学试卷(文科)(解析版)
题型:解答题
设等差数列{an}的前n和为Sn,等比数列{bn}的前n和为Tn,已知a1=1,b1=1,a2b2=1,S3T3=13,求{an},{bn}的通项公式.
查看答案和解析>>
科目:gzsx
来源:昆明模拟
题型:解答题
设等差数列{an}的前n和为Sn,等比数列{bn}的前n和为Tn,已知a1=1,b1=1,a2b2=1,S3T3=13,求{an},{bn}的通项公式.
查看答案和解析>>
科目:gzsx
来源:
题型:
在等差数列{a
n}和等比数列{b
n}中,a
1=1,b
1=2,b
n>0(n∈N
*),且b
1,a
2,b
2成等差数列,a
2,b
2,a
3+2成等比数列.
(Ⅰ)求数列{a
n}、{b
n}的通项公式;
(Ⅱ)设
cn=abn,数列{c
n}的前n和为S
n,若
>an+t对所有正整数n恒成立,求常数t的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列{a
n}和{b
n}满足a
1=2,a
n-1=a
n(a
n+1-1),b
n=a
n-1,数列{b
n}的前n和为S
n.
(1)求数列{b
n}的通项公式;
(2)设T
n=S
2n-S
n,求证:T
n+1>T
n;
(3)求证:对任意的n∈N
*有
1+≤S2n≤+n成立.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列{a
n}和{b
n}满足a
1=2,a
n-1=a
n(a
n+1-1),b
n=a
n-1,n∈N
*.
(1)求数列{b
n}的通项公式;
(2)设c
n=b
2n-1b
2n+1,求使得
| n |
 |
| i=1 |
ci<对一切n∈N
*都成立的最小正整数m;
(3)设数列{b
n}的前n和为S
n,T
n=S
2n-S
n,试比较T
n+1与T
n的大小.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列{a
n},{b
n)满足a
1=2,b
1=1,且
| | an=an-1+bn-1+1 | | bn=an-1+bn-1+1 |
| |
(n≥2),数列{c
n}满足c
n=a
n+b
n(1)求c
1和c
2的值;
(2)求证:数列 {c
n}为等差数列,并求出数列{c
n}的通项公式;
(3)设数列{c
n}的前n和为S
n,求证:
+
+
+…+
<1.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列{a
n}的前n项的“均倒数”(即平均数的倒数)为
,
(1)求{a
n}的通项公式;
(2)已知b
n=
tan(t>0),数列{b
n}的前n项为S
n,求
的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=x
2+ax+b(a,b∈R),不等式|f(x)|≤|2x
2+4x-30|对∀x∈R恒成立,数列{a
n}满足:
a1=,
2an=f(an-1)+15 (n≥2,n∈N*),数列{b
n}满足:
bn= (n∈N*).
(Ⅰ)求a,b的值;
(Ⅱ)设数列{b
n}的前n和为S
n,前n的积为T
n,求
Sn+2n+1Tn的值.
查看答案和解析>>
科目:gzsx
来源:2008-2009学年湖北省天门中学高二(下)5月月考数学试卷(A卷)(解析版)
题型:解答题
已知数列{a
n}的前n项的“均倒数”(即平均数的倒数)为
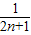
,
(1)求{a
n}的通项公式;
(2)已知b
n=

(t>0),数列{b
n}的前n项为S
n,求

的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知在数列{a
n}中,a
1=

,且有a
n+1=

(n∈N
*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn= ,数列{bn}的前n和为Sn,证明:Sn<1;
,数列{bn}的前n和为Sn,证明:Sn<1;
(Ⅲ)若 ,且{cn}的前n项和为Tn,求
,且{cn}的前n项和为Tn,求 Tn值.
Tn值.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年广东省珠海一中等六校高三(上)第二次联考数学试卷(文科)(解析版)
题型:解答题
已知数列{a
n},{b
n)满足a
1=2,b
1=1,且

(n≥2),数列{c
n}满足c
n=a
n+b
n(1)求c
1和c
2的值;
(2)求证:数列 {c
n}为等差数列,并求出数列{c
n}的通项公式;
(3)设数列{c
n}的前n和为S
n,求证:

+

+

+…+

<1.
查看答案和解析>>
科目:gzsx
来源:2011年福建省泉州市石狮市石光华侨联合中学高考数学冲刺模拟试卷2(理科)(解析版)
题型:解答题
已知函数f(x)=x
2+ax+b(a,b∈R),不等式|f(x)|≤|2x
2+4x-30|对∀x∈R恒成立,数列{a
n}满足:
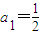
,

,数列{b
n}满足:

.
(Ⅰ)求a,b的值;
(Ⅱ)设数列{b
n}的前n和为S
n,前n的积为T
n,求

的值.
查看答案和解析>>
科目:gzsx
来源:2010年广东省揭阳市高考数学二模试卷(理科)(解析版)
题型:解答题
已知数列{a
n}和{b
n}满足a
1=2,a
n-1=a
n(a
n+1-1),b
n=a
n-1,数列{b
n}的前n和为S
n.
(1)求数列{b
n}的通项公式;
(2)设T
n=S
2n-S
n,求证:T
n+1>T
n;
(3)求证:对任意的n∈N
*有
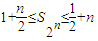
成立.
查看答案和解析>>
科目:gzsx
来源:2010年广东省汕头市潮阳一中高三数学综合试卷(理科)(解析版)
题型:解答题
已知数列{a
n}和{b
n}满足a
1=2,a
n-1=a
n(a
n+1-1),b
n=a
n-1,数列{b
n}的前n和为S
n.
(1)求数列{b
n}的通项公式;
(2)设T
n=S
2n-S
n,求证:T
n+1>T
n;
(3)求证:对任意的n∈N
*有

成立.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年广东省佛山一中高三(上)第二次段考数学试卷(文科)(解析版)
题型:解答题
已知数列{a
n},{b
n)满足a
1=2,b
1=1,且

(n≥2),数列{c
n}满足c
n=a
n+b
n(1)求c
1和c
2的值;
(2)求证:数列 {c
n}为等差数列,并求出数列{c
n}的通项公式;
(3)设数列{c
n}的前n和为S
n,求证:

+

+

+…+

<1.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知数列{an}的前n项的“均倒数”(即平均数的倒数)为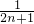 ,
,
(1)求{an}的通项公式;
(2)已知bn=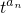 (t>0),数列{bn}的前n项为Sn,求
(t>0),数列{bn}的前n项为Sn,求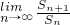 的值.
的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
在数列{an}中, .
.
(1)试判断数列{ }是否为等差数列;
}是否为等差数列;
(2)设{bn}满足bn= ,求数列{bn}的前n项为Sn;
,求数列{bn}的前n项为Sn;
(3)若 ,对任意n≥2的整数恒成立,求实数λ的取值范围.
,对任意n≥2的整数恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年广东省六校高三(上)第二次联考数学试卷(文科)(解析版)
题型:解答题
已知数列{a
n},{b
n)满足a
1=2,b
1=1,且

(n≥2),数列{c
n}满足c
n=a
n+b
n(1)求c
1和c
2的值;
(2)求证:数列 {c
n}为等差数列,并求出数列{c
n}的通项公式;
(3)设数列{c
n}的前n和为S
n,求证:

+

+

+…+

<1.
查看答案和解析>>


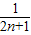 ,
, (t>0),数列{bn}的前n项为Sn,求
(t>0),数列{bn}的前n项为Sn,求 的值.
的值.![]() ,数列{bn}的前n和为Sn,证明:Sn<1;
,数列{bn}的前n和为Sn,证明:Sn<1;![]() ,且{cn}的前n项和为Tn,求
,且{cn}的前n项和为Tn,求![]() Tn值.
Tn值. (n≥2),数列{cn}满足cn=an+bn
(n≥2),数列{cn}满足cn=an+bn +
+ +
+ +…+
+…+ <1.
<1.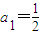 ,
, ,数列{bn}满足:
,数列{bn}满足: .
. 的值.
的值.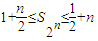 成立.
成立. 成立.
成立. (n≥2),数列{cn}满足cn=an+bn
(n≥2),数列{cn}满足cn=an+bn +
+ +
+ +…+
+…+ <1.
<1.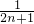 ,
,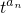 (t>0),数列{bn}的前n项为Sn,求
(t>0),数列{bn}的前n项为Sn,求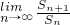 的值.
的值.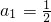 ,
, ,数列{bn}满足:
,数列{bn}满足: .
. 的值.
的值.![]() .
.![]() }是否为等差数列;
}是否为等差数列;![]() ,求数列{bn}的前n项为Sn;
,求数列{bn}的前n项为Sn;![]() ,对任意n≥2的整数恒成立,求实数λ的取值范围.
,对任意n≥2的整数恒成立,求实数λ的取值范围. (n≥2),数列{cn}满足cn=an+bn
(n≥2),数列{cn}满足cn=an+bn +
+ +
+ +…+
+…+ <1.
<1.