精英家教网 >
试题搜索列表 >如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC. (1)求证:BE=CF; (2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME. 求证:①ME⊥BC;②DE=DN
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC. (1)求证:BE=CF; (2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME. 求证:①ME⊥BC;②DE=DN答案解析
科目:czsx
来源:
题型:
如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥
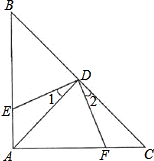
DF.
(1)求证:∠1=∠2;
(2)求证:△ADE≌△CDF;
(3)若AB=8cm,求四边形AEDF的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
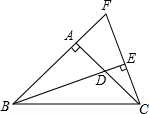
如图,△ABC中,∠BAC=90°,AB=AC,BD是∠ABC的平分线,BD的延长线垂直过C点的直线于E,直线CE交BA的延长线于F.求证:
(1)Rt△BEF≌Rt△BEC;
(2)BD=2CE.
查看答案和解析>>
科目:czsx
来源:
题型:
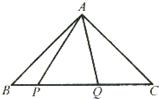
3、如图,△ABC中,∠BAC=90°,AB=AC,P、Q是BC上两点,且满足BP
2+CQ
2=PQ
2,则∠PAQ的度数是
45
°.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点.
(1)如图①,若点E,F分别在边AB,AC上,且AE=CF,连接DE,DF,EF,观察,猜想△DEF是否为等腰直角三角形,并证明你的猜想.
(2)如图②,若点E,F分别在边AB,CA的延长线上,且AE=CF,连接DE,DF,EF,那么(1)中所得到的结论还成立吗?如果成立,请给出证明;如果不成立,说明你的理由.

查看答案和解析>>
科目:czsx
来源:
题型:
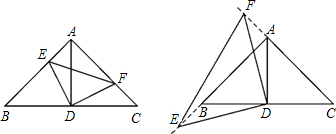
如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点.
(1)如图1,若E、F分别是AB、AC上的点,且AE=CF.求证:①△AED≌△CFD;②△DEF为等腰直角三角形.
(2)如图2,点F、E分别D在CA、AB的延长线上,且AE=CF,猜想△DEF是否为等腰直角三角形?如果是请给出证明.
查看答案和解析>>
科目:czsx
来源:
题型:

16、已知,如图,△ABC中,∠BAC=90°,AB=AC,D为AC上一点,且∠BDC=124°,延长BA到点E,使AE=AD,BD的延长线交CE于点F,求∠E的度数.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于点E,则BD与DE、CE有什么数量关系?并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,△ABC中,∠BAC=90°,AB=AC.
(1)只用直尺(没有刻度)和圆规,作出∠A的平分线AD和AB边上的中线CE(要求保留作图痕迹,不必写出作法);
(2)完成(1)题的作图后,若AB=AC=2,在AD上存在一点P,可以使得BP+EP最小,作出这个点P(不必写出理由),并写出这个最小值.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC上一个动点(不与B、C重合),在AC上取
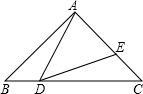
E点,使∠ADE=45度.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当:△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:czsx
来源:
题型:
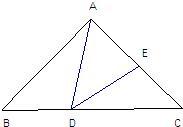
23、如图,△ABC中,∠BAC=90°,AB=AC,D在BC上,E在AC上,且∠ADE=45度.
(1)求证:△ABD∽△DCE.
(2)当D在什么位置时,△ABD≌△DCE.
查看答案和解析>>
科目:czsx
来源:
题型:

3、如图,△ABC中,∠BAC=90°,AB=AC,△ABC按顺时针方向旋转一个角度后,成为△ACD,则图中的
A
是旋转中心,旋转角是
270°
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC上一个动点(不与B、C重合),在AC上取E点,使∠ADE=45°.
(1)试判断△ABD与△DCE是否相似并说明理由;
(2)设BD=x,AE=y,求y关于x的函数关系式;并指出当点D在BC上运动(不与B、C重合)时,AE是
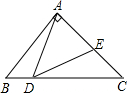
否存在最小值?若存在,求出最小值;若不存在,说明理由;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:czsx
来源:
题型:
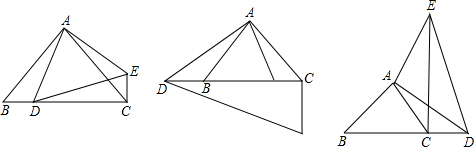
如图,△ABC中,∠BAC=90°,AB=AC,点D在直线BC上,△ADE是等腰直角三角形,∠DAE=90°,AD=AE,连接CE.
(1)当点D在线段BC上时(如图1),求证:DC+CE=
AC;
(2)当点D在线段CB延长线上时(如图2);当点D在线段BC延长线上时(如图3),探究线段DC、CE、AC之间的数量关系分别为,图2:
; 图3:
;
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•金华模拟)如图,△ABC中,∠BAC=90°,AB=AC.P是AB的中点,正方形ADEF的边在线段CP上,则正方形ADEF与△ABC的面积的比为
.
查看答案和解析>>
科目:czsx
来源:期末题
题型:解答题
如图,△ABC中,∠BAC=90°.AB=AC,D在AC上,E在BA上,BD=CE,求证:BE=CD.
查看答案和解析>>
科目:czsx
来源:不详
题型:填空题
如图,△ABC中,∠BAC=90°,AB=AC,P、Q是BC上两点,且满足BP
2+CQ
2=PQ
2,则∠PAQ的度数是______°.
查看答案和解析>>
科目:czsx
来源:海南省月考题
题型:解答题
如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC上一个动点(不与B、C重合),在AC上取E点,使∠ADE=45度.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当:△ABD∽△DCE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
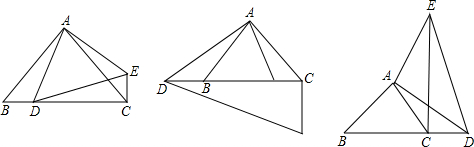
如图,△ABC中,∠BAC=90°,AB=AC,点D在直线BC上,△ADE是等腰直角三角形,∠DAE=90°,AD=AE,连接CE.
(1)当点D在线段BC上时(如图1),求证:DC+CE= AC;
AC;
(2)当点D在线段CB延长线上时(如图2);当点D在线段BC延长线上时(如图3),探究线段DC、CE、AC之间的数量关系分别为,图2:______; 图3:______;
查看答案和解析>>
科目:czsx
来源:期中题
题型:解答题
如图在△ABC中,

BAC= 90

,AB =AC,若MN是经过点A的直线,BD

MN于点D,CE

MN于点E,
(1)求证:BD= AE.
(2)若将MN绕点A旋转,使MN与BC相交于点O,其他条件都不变,BD与AE还相等吗?为什么?
(3)BD、CE与DE有何关系?
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:044
如图,△ABC中,∠BAC=90°,AB=AC,将△ABC绕顶点A旋转,使AB旋转到AC的位置.
(1)画出旋转后的 .
.
(2)写出旋转角的度数

查看答案和解析>>

 DF.
DF.  如图,△ABC中,∠BAC=90°,AB=AC,BD是∠ABC的平分线,BD的延长线垂直过C点的直线于E,直线CE交BA的延长线于F.求证:
如图,△ABC中,∠BAC=90°,AB=AC,BD是∠ABC的平分线,BD的延长线垂直过C点的直线于E,直线CE交BA的延长线于F.求证:

 16、已知,如图,△ABC中,∠BAC=90°,AB=AC,D为AC上一点,且∠BDC=124°,延长BA到点E,使AE=AD,BD的延长线交CE于点F,求∠E的度数.
16、已知,如图,△ABC中,∠BAC=90°,AB=AC,D为AC上一点,且∠BDC=124°,延长BA到点E,使AE=AD,BD的延长线交CE于点F,求∠E的度数. 如图,△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于点E,则BD与DE、CE有什么数量关系?并证明你的结论.
如图,△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于点E,则BD与DE、CE有什么数量关系?并证明你的结论. 如图,△ABC中,∠BAC=90°,AB=AC.
如图,△ABC中,∠BAC=90°,AB=AC. E点,使∠ADE=45度.
E点,使∠ADE=45度. 23、如图,△ABC中,∠BAC=90°,AB=AC,D在BC上,E在AC上,且∠ADE=45度.
23、如图,△ABC中,∠BAC=90°,AB=AC,D在BC上,E在AC上,且∠ADE=45度. 否存在最小值?若存在,求出最小值;若不存在,说明理由;
否存在最小值?若存在,求出最小值;若不存在,说明理由;
 (2013•金华模拟)如图,△ABC中,∠BAC=90°,AB=AC.P是AB的中点,正方形ADEF的边在线段CP上,则正方形ADEF与△ABC的面积的比为
(2013•金华模拟)如图,△ABC中,∠BAC=90°,AB=AC.P是AB的中点,正方形ADEF的边在线段CP上,则正方形ADEF与△ABC的面积的比为
 AC;
AC;
 BAC= 90
BAC= 90 ,AB =AC,若MN是经过点A的直线,BD
,AB =AC,若MN是经过点A的直线,BD MN于点D,CE
MN于点D,CE MN于点E,
MN于点E,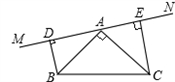
 .
.