
9.已知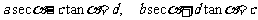
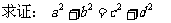
证:由题设: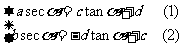
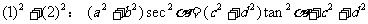
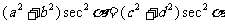
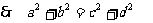
8.求证: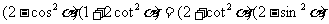
证明:可先证: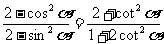 (※)
(※)
右式=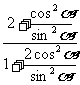 =
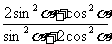
=
=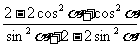 =
=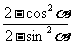 =左式
=左式
∴(※)式成立,即原等式成立.
3.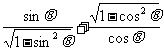
分析:在化简前应先复习“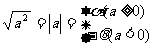 ”以及绝对值的概念.
”以及绝对值的概念.
解:(1)原式=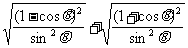
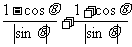
=
=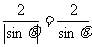
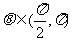
(2)原式=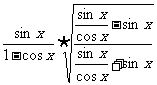
=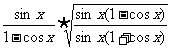
=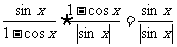
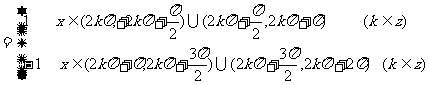
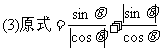
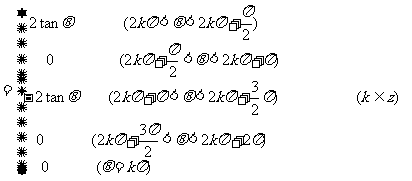
说明:在三角式的化简或恒等变形中,正确处理算术根和绝对值问题是个难点.这是由于算术根和绝对值的概念在初中代数阶段是一个不易理解和掌握的基本概念,现在又以三角式的形式出现,就更增加了它的复杂性和抽象性,所以形成新的难点.为处理好这个问题,要先复习算术根和绝对值的定义.
2.
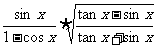
1.
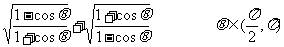
6.已知tan =3,求下列各式的值
=3,求下列各式的值

分析:思路1,可以由tan =3求出sin
=3求出sin 、cos
、cos 的值,代入求解即可;
的值,代入求解即可;
思路2,可以将要求值的表达式利用同角三角函数关系,变形为含tan 的表达式.
的表达式.
解:(1)原式分子分母同除以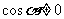 得,
得,
原式=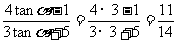
(2)原式的分子分母同除以
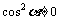 得:
得:
原式=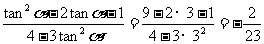
(3)用“1”的代换
原式=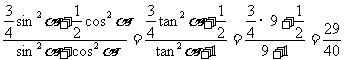
(4)原式=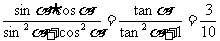
(5)  =
=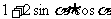 =
=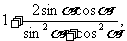
=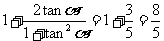
∴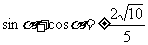
(6)同(5)
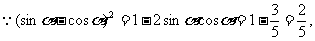
∴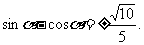
(7)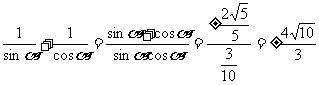

(8) =
=
=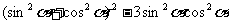
=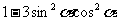 =
=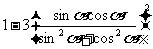
=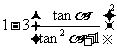 =
=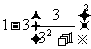 =
=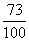
说明:数字“1”的代换,表面上看增加了运算,但同时它又可以将原表达式整体结构发生改变,给解决问题带来方面,故解题时,应给于足够的认识.
7 化简下列各式
化简下列各式
5.已知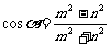 ,求tan
,求tan 和sin
和sin 的值.
的值.
分析:由已知条件可知cos 的值可能正可能负,
的值可能正可能负,
∴要分别讨论分子为正、为负的情形.
解:(1)若│m│>│n│>0
则cos >0 ∴
>0 ∴ 在Ⅰ、Ⅳ象限
在Ⅰ、Ⅳ象限
当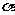 在第Ⅰ象限时
在第Ⅰ象限时


当 在第Ⅳ象限时
在第Ⅳ象限时
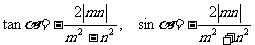

(2)若0<│m│<│n│时,则cos <0 ∴
<0 ∴ 在第II、III象限
在第II、III象限
当 在第Ⅱ象限时
在第Ⅱ象限时
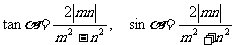

当 在第III象限时
在第III象限时


(3)若n=0、m≠0时,tan =0,sin
=0,sin =0
=0
(4) 若m=0、n≠0时,tan =0,sin
=0,sin =0
=0
说明:已知某角的一个三角函数值,求该角的其他三角函数值时要注意:
(1) 角所在的象限;
(2) 用平方关系求值时,所求三角函数的符号由角所在的象限决定;
(3)若题设中已知角的某个三角函数值是用字母给出的,则求其他函数值时,要对该字母分类讨论.
4.已知 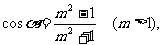 求cot
求cot 的值
的值
分析:由题意可知cos >0,∴分
>0,∴分 在Ⅰ、Ⅳ象限讨论.利用平方关系可求正弦值,利用商的关系,即可求余切值.
在Ⅰ、Ⅳ象限讨论.利用平方关系可求正弦值,利用商的关系,即可求余切值.
解:∵ m>1 ∴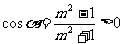 ,∴
,∴ 在第I、IV象限
在第I、IV象限
当α在第I象限时
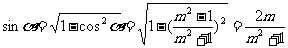
∴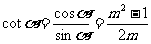
当 在第IV象限时,
在第IV象限时,
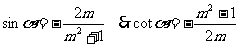
3.已知角 的终边在直线y=3x上,求sin
的终边在直线y=3x上,求sin 和cos
和cos 的值.
的值.
解:由题意可知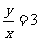
∵角 的终边在直线y=3x上
的终边在直线y=3x上
∴设P(a,3a)(a≠0)为角 终边上的任一点.
终边上的任一点.
当 在第一象限时,a>0
在第一象限时,a>0
∴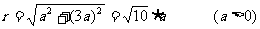
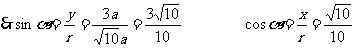
当 在第三象限,
在第三象限,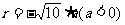
∴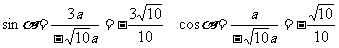
2.已知: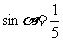 且
且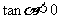 ,试用定义求
,试用定义求 的其余三个三角函数值.
的其余三个三角函数值.
分析:题目要用定义求三角函数值,则解决问题的关键应找到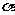 终边的所在象限.
终边的所在象限.
解:∵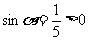 ,而
,而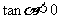
∴ 在第二象限
在第二象限
设点P(x,y)为角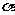 终边上任一点
终边上任一点
由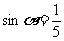 ,可设
,可设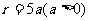 ,则
,则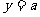 .
.
∴
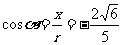 ,
,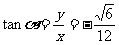 ,
,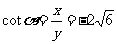 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com