
1(汉沽一中2008~2009届月考文6). 极坐标方程分别是ρ=cosθ和ρ=sinθ 的两个圆的圆心距是( D )
A.2
B.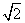 C. 1
D.
C. 1
D.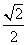
2 (武清区2008~2009学年度期中理)
(武清区2008~2009学年度期中理)

B
3(武清区2008~2009学年度期中理)
C
4(武清区2008~2009学年度期中理)
D
1(汉沽一中2008~2008学年月考理7). 已知变量a,b已被赋值,要交换a、b的值,采用的算法是D
A.a=b, b=a B.a=c, b=a, c=b C.a=c, b=a, c=a D.c=a, a=b, b=c
 2
2 (2009年滨海新区五所重点学校联考文8).某流程如右图所示,现输入如下四个函数,
(2009年滨海新区五所重点学校联考文8).某流程如右图所示,现输入如下四个函数,
则可以输出的函数是(8.D )
A.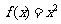 B.
B.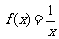
C.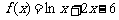 D.
D.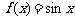
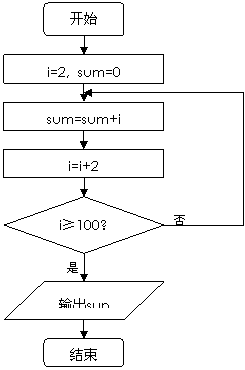 3(汉沽一中2008~2009届月考文10). 给出下面的程序框图,那么,输出的数是(A )
3(汉沽一中2008~2009届月考文10). 给出下面的程序框图,那么,输出的数是(A )
A.2450 B. 2550
C. 5050 D. 4900
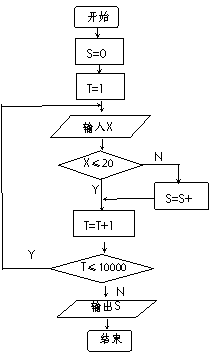 4(汉沽一中2008~2009届月考理7).为调查深圳市中学生平均每人每天参加体育锻炼时间
4(汉沽一中2008~2009届月考理7).为调查深圳市中学生平均每人每天参加体育锻炼时间 (单位:分钟),按锻炼时间分下列4种情况统计:①0-10分钟;②11-20分钟;③21-30分钟; ④30分钟以上.有10000名中学生参加了此项调查活动,右图是此次调查中某一项的流程图,其输出的结果是6200.则平均每天参加体育锻炼时间在0-20分钟内的学生的频率是(C)
(单位:分钟),按锻炼时间分下列4种情况统计:①0-10分钟;②11-20分钟;③21-30分钟; ④30分钟以上.有10000名中学生参加了此项调查活动,右图是此次调查中某一项的流程图,其输出的结果是6200.则平均每天参加体育锻炼时间在0-20分钟内的学生的频率是(C)
A.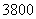
B.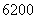
C.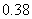
|
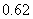
1(2009年滨海新区五所重点学校联考文19).( 本小题满分12分) 如图,在棱长为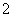 的正方体
的正方体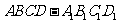 中,
中,
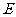 、
、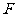 分别为
分别为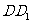 、
、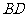 的中点。
的中点。
(Ⅰ)求证: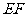 //平面
//平面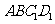
(Ⅱ)求证: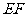 ⊥
⊥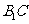
(Ⅲ)求三棱锥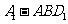 的体积
的体积
19.(本小题满分12分)
解:
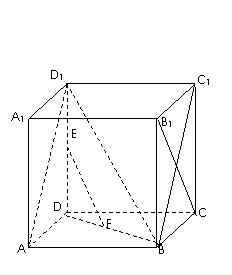 (Ⅰ)连结BD1,在△DD1B中,E、F分别为D1D,
(Ⅰ)连结BD1,在△DD1B中,E、F分别为D1D,
DB的中点,则EF//D1B。 ………………2分
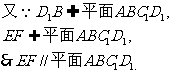
………………4分
(Ⅱ)∵B1C⊥AB,B1C⊥BC1,………………5分
AB 平面ABC1D1,BC1
平面ABC1D1,BC1 平面ABC1D1,
平面ABC1D1,
AB∩BC1=B,
∴B1C⊥平面ABC1D1。 ………………7分
又∵BD1 平面ABC1D1,
平面ABC1D1,
∴B1C⊥BD1, ………………8分
而EF//BD1,∴EF⊥B1C。………………9分
(Ⅲ)三棱锥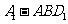 的体积
的体积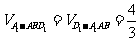 ………………12分
………………12分
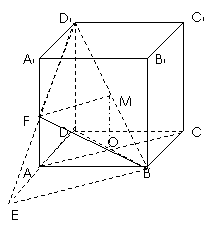
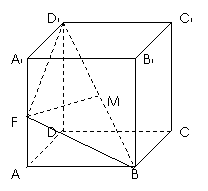 2(汉沽一中2008~2009届月考文18).(本小题满分14分)如图,已知棱柱
2(汉沽一中2008~2009届月考文18).(本小题满分14分)如图,已知棱柱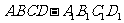 的底面是菱形,且
的底面是菱形,且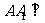 面
面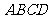 ,
,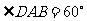 ,
,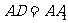 ,
,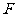 为棱
为棱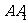 的中点,
的中点,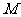 为线段
为线段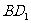 的中点,
的中点,
(1)求证: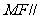 面
面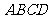 ;
;
(2)求证: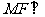 面
面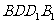 ;
;
(3)求面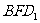 与面
与面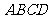 所成二面角的大小.
所成二面角的大小.
 (1)证明:连结
(1)证明:连结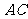 、
、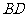 交于点
交于点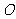 ,再连结
,再连结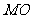 ………………………………………………1分
………………………………………………1分
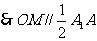 且
且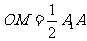 , 又
, 又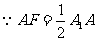 ,
,
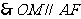 且
且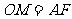
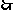 四边形
四边形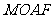 是平行四边形,
是平行四边形,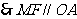 …………… 3分
…………… 3分
又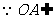 面
面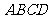
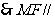 面
面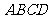 ……………………………… 4分
……………………………… 4分
(2)证明: 底面是菱形,
底面是菱形, 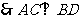 ………… 5分
………… 5分
又 面
面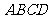 ,
,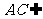 面
面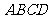
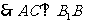 ,
,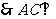 面
面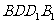 ………………………………………………6分
………………………………………………6分
又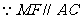
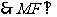 面
面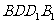 ………………………………8分
………………………………8分
(3)延长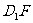 、
、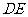 交于点
交于点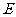 ………………………………9分
………………………………9分
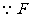 是
是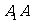 的中点且
的中点且 是菱形
是菱形
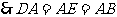
又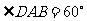
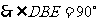 ………………………………10分
………………………………10分
由三垂线定理可知 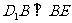
 为所求角 ……………………………………………12分
为所求角 ……………………………………………12分
在菱形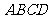 中,
中,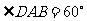
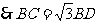
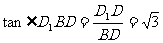
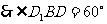 …………………………………………………14分
…………………………………………………14分
3(汉沽一中2008~2009届月考理17).(本小题满分14分)
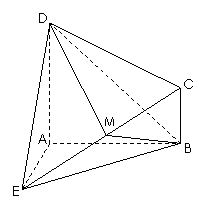 如图所示的几何体
如图所示的几何体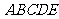 中,
中,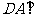 平面
平面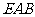 ,
,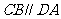 ,
,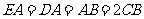 ,
,
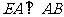 ,
,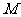 是
是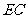 的中点.
的中点.
(Ⅰ)求证: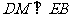 ;
;
(Ⅱ)求二面角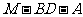 的余弦值.
的余弦值.
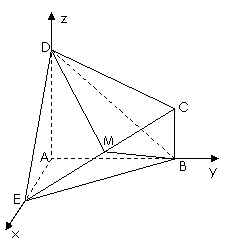 解法一: 分别以直线
解法一: 分别以直线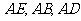 为
为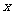 轴、
轴、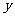 轴、
轴、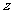 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系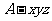 ,设
,设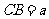 ,则
,则
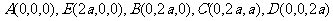 ,
,
所以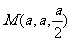 . ………………………… 4分
. ………………………… 4分
(Ⅰ)证: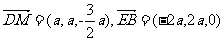 …… 5分
…… 5分
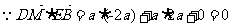 …… 6分
…… 6分
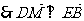 ,即
,即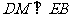 .……………………… 7分
.……………………… 7分
(Ⅱ)解:设平面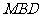 的法向量为
的法向量为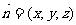 ,
,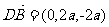
由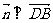 ,
, 得
得
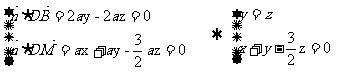
取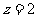 得平面
得平面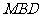 的一非零法向量为
的一非零法向量为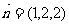 ………………………… 10分
………………………… 10分
又平面BDA的法向量为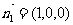 …………………………………… 11分
…………………………………… 11分
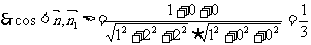 ,
,
∴二面角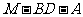 的余弦值为
的余弦值为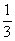 .
…………………………… 14分
.
…………………………… 14分
 解法二:
解法二:
(Ⅰ)证明:取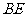 的中点
的中点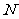 ,连接
,连接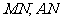 ,则
,则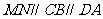 ,
,
故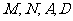 四点共面,
………………………… 2分
四点共面,
………………………… 2分
∵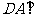 平面
平面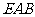 ,
,
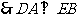 .
………………………… 3分
.
………………………… 3分
又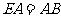
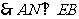 ………………………… 4分
………………………… 4分
由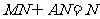 ,
,
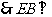 平面
平面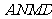 ………………………… 6分
………………………… 6分
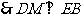 ;
……………………… 7分
;
……………………… 7分
(Ⅱ)取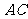 的中点
的中点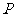 ,连
,连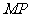 ,则
,则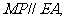
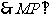 平面
平面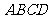
过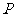 作
作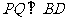 ,连
,连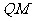 ,则
,则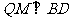
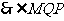 是二面角
是二面角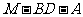 的平面角.
……………………… 9分
的平面角.
……………………… 9分
设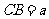 ,
, 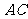 与
与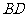 的交点为
的交点为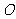 ,记
,记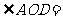
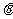 ,
,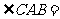
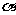 ,则有
,则有
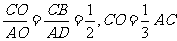
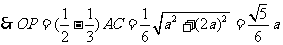 .
.
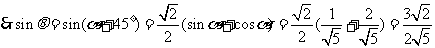 .
.
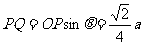 ,
…………………… 12分
,
…………………… 12分
又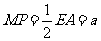
在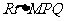 中,
中,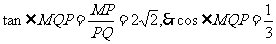
即二面角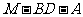 的余弦值为
的余弦值为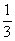 .
…………………… 14分
.
…………………… 14分
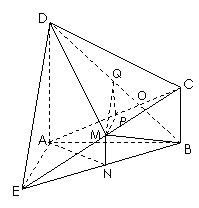
4(汉沽一中2008~2008学年月考理17).(本小题满分14分)
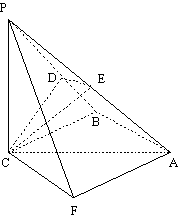
如图,三棱锥P-ABC中, PC 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD 平面PAB.
平面PAB.
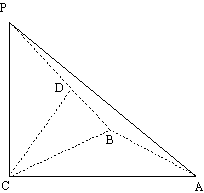 (I) 求证:AB
(I) 求证:AB 平面PCB;
平面PCB;
(II) 求异面直线AP与BC所成角的大小;
(III)求二面角C-PA-B的大小.
解法一:(I) ∵PC 平面ABC,
平面ABC, 平面ABC,
平面ABC,
∴PC AB.…………………………2分
AB.…………………………2分
 ∵CD
∵CD 平面PAB,
平面PAB,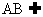 平面PAB,
平面PAB,
∴CD AB.…………………………4分
AB.…………………………4分
又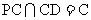 ,
,
∴AB 平面PCB. …………………………5分
平面PCB. …………………………5分
(II) 过点A作AF//BC,且AF=BC,连结PF,CF.
则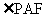 为异面直线PA与BC所成的角.………6分
为异面直线PA与BC所成的角.………6分
由(Ⅰ)可得AB⊥BC,
∴CF AF.
AF.
由三垂线定理,得PF AF.
AF.
则AF=CF=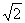 ,PF=
,PF=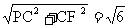 ,
,
在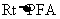 中, tan∠PAF=
中, tan∠PAF=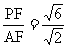 =
=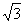 ,
,
∴异面直线PA与BC所成的角为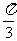 .…………………………………9分
.…………………………………9分
(III)取AP的中点E,连结CE、DE.
∵PC=AC=2,∴CE  PA,CE=
PA,CE=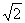 .
.
∵CD 平面PAB,
平面PAB,
由三垂线定理的逆定理,得 DE  PA.
PA.
∴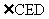 为二面角C-PA-B的平面角.…………………………………11分
为二面角C-PA-B的平面角.…………………………………11分
由(I) AB 平面PCB,又∵AB=BC,可求得BC=
平面PCB,又∵AB=BC,可求得BC=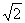 .
.
在 中,PB=
中,PB=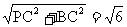 ,
,
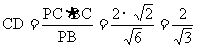 .
.
 在
在 中, sin∠CED=
中, sin∠CED= .
.
∴二面角C-PA-B的大小为arcsin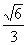 .……14分
.……14分
解法二:(I)同解法一.
(II) 由(I) AB 平面PCB,∵PC=AC=2,
平面PCB,∵PC=AC=2,
又∵AB=BC,可求得BC=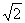 .
.
以B为原点,如图建立坐标系.
则A(0,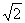 ,0),B(0,0,0),
,0),B(0,0,0),
C(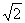 ,0,0),P(
,0,0),P(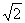 ,0,2).
,0,2).
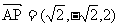 ,
,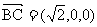 .
.
…………………7分
则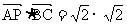 +0+0=2.
+0+0=2.
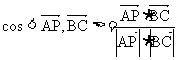 =
=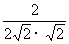 =
= 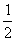 .
.
∴异面直线AP与BC所成的角为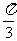 .………………………10分
.………………………10分
(III)设平面PAB的法向量为m= (x,y,z).
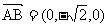 ,
,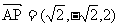 ,
,
则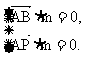 即
即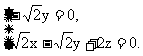

解得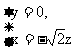 令
令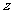 = -1, 得
m= (
= -1, 得
m= (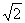 ,0,-1).
,0,-1).
设平面PAC的法向量为n=(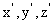 ).
).
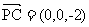 ,
,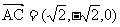 ,
,
则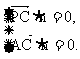 即
即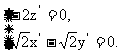
解得 令
令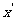 =1, 得
n= (1,1,0).……………………………12分
=1, 得
n= (1,1,0).……………………………12分
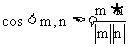 =
=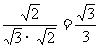 .
.
∴二面角C-PA-B的大小为arccos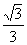 .………………………………14分
.………………………………14分
5(和平区2008年高考数学(理)三模19). (本小题满分12分)
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE。
(1)求证:AE⊥平面BCE;
(2)求二面角B-AC-E的大小;
(3)求点D到平面ACE的距离。
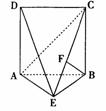
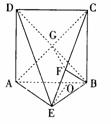
解:(1)如图,∵ BF⊥平面ACE ∴ BF⊥AE(1分)
又∵ 二面角D-AB-E为直二面角,且CB⊥AB
∴ CB⊥平面ABE ∴ CB⊥AE
∵ 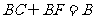 ∴ AE⊥平面BCE(3分)
∴ AE⊥平面BCE(3分)
(2)连BD交AC于G,连FG
∵ 正方形ABCD边长为2 ∴ BG⊥AC,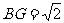
∵ BF⊥平面ACE 由三垂线定理逆定理得FG⊥AC
∴ ∠BGF是二面角B-AC-E的平面角(5分)
由(1)AE⊥平面BCE ∴ AE⊥EB
又∵ AE=EB ∴
在等腰直角三角形AEB中,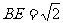
又∵ Rt△BCE中,
∴ 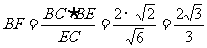 (7分)
(7分)
∴ 在Rt△BFG中,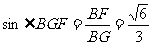
∴ 二面角B-AC-E等于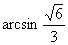 (8分)
(8分)
(3)过E作EO⊥AB于O,OE=1
∵ 二面角D-AB-E为直二面角
∴ EO⊥平面ABCD(9分)
设D到平面ACE的距离为h
∵ 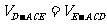 ∴
∴ 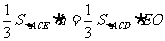
∵ AE⊥平面BCE ∴ AE⊥EC
∴ 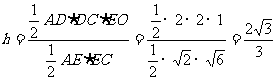
∴ 点D到平面ACE的距离为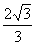 (12分)
(12分)

1(汉沽一中2008~2009届月考理11).在直角三角形 中,两直角边分别为
中,两直角边分别为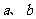 ,设
,设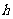 为斜边上的高,则
为斜边上的高,则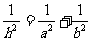 ,由此类比:三棱锥
,由此类比:三棱锥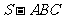 的三个侧棱
的三个侧棱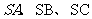 两两垂直,且长分别为
两两垂直,且长分别为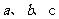 ,设棱锥底面
,设棱锥底面 上的高为
上的高为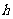 ,则
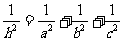
.
,则
. 
2(汉沽一中2008~2008学年月考理11).一个正四棱锥的底面边长为2,侧棱长为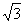 ,五个顶点都在同一个球面上,则此球的表面积为
. 9π
,五个顶点都在同一个球面上,则此球的表面积为
. 9π
3(和平区2008年高考数学(理)三模12). 在120°的二面角内放一个半径为6的球,与两个半平面各有且仅有一个公共点,则这两点间的球面距离是 。2
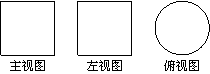
1(汉沽一中2008~2009届月考理 3).如右图所示,一个空间几何体的主视图和左视图都是边长为 的正方形,俯视图是一个直径为
的正方形,俯视图是一个直径为 的圆,那么这个几何体的全面积为(A)
的圆,那么这个几何体的全面积为(A)
 A.
A.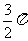 B.
B.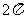
C.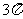 D.
D.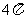
2 (汉沽一中2008~2009届月考文5). 一条直线若同时平行于两个相交平面,则这条直线与这两个平面交线的位置关系是( C )
(汉沽一中2008~2009届月考文5). 一条直线若同时平行于两个相交平面,则这条直线与这两个平面交线的位置关系是( C )
A.异面 B. 相交 C. 平行 D. 不确定
3(和平区2008年高考数学(理)三模6). 如果直线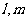 与平面
与平面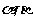 ,
,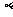 满足:
满足: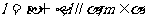 和
和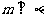 ,那么必有(B )
,那么必有(B )
A. 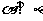 且
且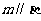 B.
B.
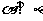 且
且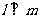
C. 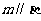 且
且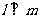 D.
D.
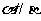 且
且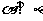
4(汉沽一中2008~2008学年月考理6).三棱锥D-ABC的三个侧面分别与底面全等,且AB=AC=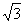 ,BC=2,则二面角A-BC-D的大小为D
,BC=2,则二面角A-BC-D的大小为D
A. 300 B. 450 C.600 D.900
1(汉沽一中2009届月考文19).(本小题满分12分)关于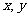 的方程
的方程
(1)若方程C表示圆,求实数m的取值范围;
(2)在方程C表示圆时,若该圆与直线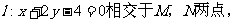 且
且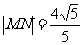 ,求实数m的值;
,求实数m的值;
(3)在(2)的条件下,若定点A的坐标为(1,0),点P是线段MN上的动点,求直线AP的斜率的取值范围。
解:(1)方程C可化为: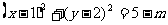
要使该方程表示圆,只需5-m>0.即m<5.
所以方程C表示圆时,实数m的取值范围是 。
4分
。
4分
(2)由(1)知,当方程C表示圆时,圆心为C(1,2),
半径为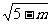 。过圆心C作直线L的垂线CD,D为垂足。
。过圆心C作直线L的垂线CD,D为垂足。
则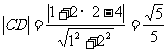
 又由
又由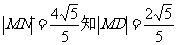 6分
6分
因为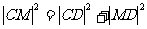 。
。
所以 ,
,
解得m=4. 8分
(3)由(2)得C圆的方程为: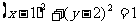
再由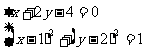
得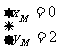 和
和 10分
10分
所以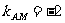 ,
,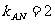
由图象可知,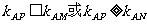
所以直线AP的斜率的取值范围是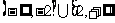 。
12分
。
12分
.
1(一中2008-2009月考理11).圆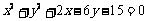 与直线
与直线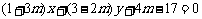 的交点个数是__ 。2
的交点个数是__ 。2
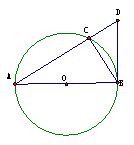 2(2009年滨海新区五所重点学校联考理12).已知圆O直径为10,AB是圆O的直径,C为圆O上一点,且BC=6,
2(2009年滨海新区五所重点学校联考理12).已知圆O直径为10,AB是圆O的直径,C为圆O上一点,且BC=6,
过点B的圆O的切线交AC延长线于点D,则 DA=______________;12. 12.5
3(2009年滨海新区五所重点学校联考理14). 圆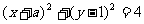 被直线
被直线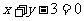 截得的弦长为
截得的弦长为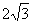 ,则
,则 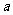 = .
= .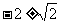
4(汉沽一中2008~2008学年月考理12).与直线2x-y-4=0平行且与曲线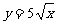 相切的直线方程是 .16x-8y+25=0
相切的直线方程是 .16x-8y+25=0
5(汉沽一中2009届月考文15).已知圆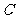 的圆心与点
的圆心与点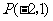 关于直线
关于直线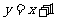 对称.直
对称.直
线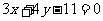 与圆
与圆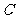 相交于
相交于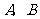 两点,且
两点,且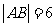 ,则圆
,则圆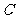 的方程为
.
的方程为
. 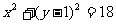
1(一中2008-2009月考理2).“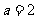 ”是“直线
”是“直线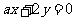 平行于直线
平行于直线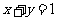 ”的
( C )
”的
( C )
A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
2  (一中2008-2009月考理3).从点
(一中2008-2009月考理3).从点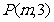 向圆
向圆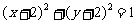 引切线,则一条切线长的最小值为
( A )
引切线,则一条切线长的最小值为
( A )
A.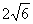 B.5 C.
B.5 C.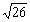 D.
D.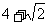
3(汉沽一中2009届月考文4).经过圆x2+2x+y2=0的圆心G,且与直线x+y=0垂直的直线方程是( A )
A .x-y+1=0 B .x-y-1=0 C .x+y-1=0 D .x+y+1=0
4(和平区2008年高考数学(文)三模8). 已知半径为1的圆的圆心在双曲线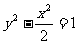 上,当圆心到直线
上,当圆心到直线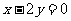 的距离最少时,该圆的方程为( A
)
的距离最少时,该圆的方程为( A
)
A. 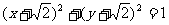 或
或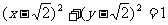
B. 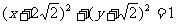
C. 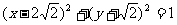
D.  或
或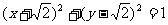
5(和平区2008年高考数学(理)三模)9. 若圆 和圆
和圆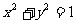 关于直线
关于直线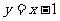 对称,动圆P与圆C相外切且与直线
对称,动圆P与圆C相外切且与直线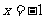 相切,则动圆P的圆心的轨迹方程是(C )
相切,则动圆P的圆心的轨迹方程是(C )
A. 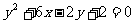 B.
B.
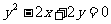
C.  D.
D.

6(汉沽一中2008~2008学年月考理8).已知点M(-3,0),N(3,0),B(1,0),圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程为B
A.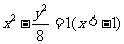 B.
B.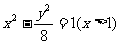
C.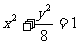 (x > 0) D.
(x > 0) D.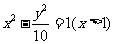
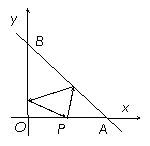 9(汉沽一中2008~2009届月考理
8).如右图,已知
9(汉沽一中2008~2009届月考理
8).如右图,已知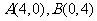 ,从点
,从点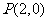 射出的光线经直线
射出的光线经直线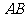 反射后再射到直线
反射后再射到直线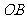 上,最后经直线
上,最后经直线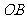 反射又回到
反射又回到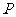 点,则光线所经过的路程是(A)
点,则光线所经过的路程是(A)
A.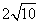
B.
C.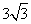
D.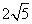
1(汉沽一中2008~2009届月考文16).(本小题满分12分)将 、
、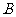 两枚骰子各抛掷一次,观察向上的点数,问:
两枚骰子各抛掷一次,观察向上的点数,问:
(1)共有多少种不同的结果?
(2)两数之和是3的倍数的结果有多少种?
(3)两数之和是3的倍数的概率是多少?
解:(1)共有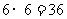 种结果;
……………………………………4分
种结果;
……………………………………4分
(2)共有12种结果; ……………………………………8分
(3)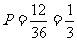 .
………………………………………12分
.
………………………………………12分
2(2009年滨海新区五所重点学校联考理18).(本题满分12分)甲、乙两人进行摸球游戏,一袋中装有2个黑球和1个红球。规则如下:若一方摸中红球,将此球放入袋中,此人继续摸球;若一方没有摸到红球,将摸到的球放入袋中,则由对方摸彩球。现甲进行第一次摸球。
(Ⅰ)在前三次摸球中,甲恰好摸中一次红球的所有情况;
(Ⅱ)在前四次摸球中,甲恰好摸中两次红球的概率。;
(Ⅲ)设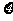 是前三次摸球中,甲摸到的红球的次数,
是前三次摸球中,甲摸到的红球的次数,
求随机变量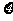 的概率分布与期望。
的概率分布与期望。
解: (Ⅰ) 甲红甲黑乙红黑均可;甲黑乙黑甲红。。。。。。。。。。2分
(Ⅱ)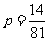 。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。6分
(Ⅲ) 设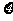 的分布是 。。。。。。。。。每求对一个1分共4分,表1分, E
的分布是 。。。。。。。。。每求对一个1分共4分,表1分, E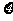 1分共6分
1分共6分
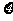 |
0 |
1 |
2 |
3 |
|
P |
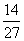 |
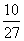 |
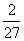 |
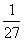 |
E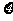 =
=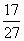 。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。12分
3(2009年滨海新区五所重点学校联考文18).(本小题满分12分)某商场举行抽奖活动,从装有编号0,1,2,3四个小球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(Ⅰ)求中三等奖的概率;
(Ⅱ)求中奖的概率.
解: 设“中三等奖”的事件为A,“中奖”的事件为B,从四个小球中有放回的取两个共有
(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),
(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)16种不同的方法。…3分
(Ⅰ)两个小球号码相加之和等于3的取法有4种:
(0,3)、(1,2)、(2,1)、(3,0)…………………4分
故 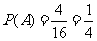 ……………………………………6分
……………………………………6分
(Ⅱ)两个小球号码相加之和等于3的取法有4种。
两个小球相加之和等于4的取法有3种:(1,3),(2,2),(3,1)
两个小球号码相加之和等于5的取法有2种:(2,3),(3,2), ………………9分
由互斥事件的加法公式得
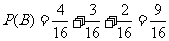 ………………12分
………………12分
4(汉沽一中2008~2009届月考理 16).(本小题满分12分)
16).(本小题满分12分)
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入 袋或
袋或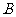 袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是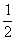 .
.
(Ⅰ)求小球落入 袋中的概率
袋中的概率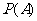 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记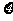 为落入
为落入
袋中小球的个数,试求 的概率和
的概率和 的数学期望
的数学期望 .
.
解: (Ⅰ)解法一:记小球落入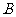 袋中的概率
袋中的概率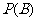 ,则
,则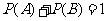 ,
,
由于小球每次遇到黑色障碍物时一直向左或者一直向右下落,小球将落入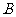 袋,所以
袋,所以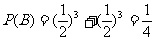 ‘…………………………………………………………………
2分
‘…………………………………………………………………
2分
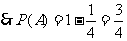 . ……………………………………………………………… 5分
. ……………………………………………………………… 5分
解法二:由于小球每次遇到黑色障碍物时,有一次向左和两次向右或两次向左和一次向右下落时小球将落入 袋.
袋.
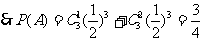 ,
……………………………… 5分
,
……………………………… 5分
(Ⅱ)由题意,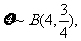 所以有 ……………………………………………… 7分
所以有 ……………………………………………… 7分
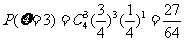 ,
……………………………………… 10分
,
……………………………………… 10分
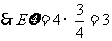 .
……………………………… 12分
.
……………………………… 12分
5(汉沽一中2008~2009届月考文16)、(本小题满分12分)
某班甲、乙两学生的高考备考成绩如下:
甲: 512 554 528 549 536 556 534 541 522 538
乙:515 558 521 543 532 559 536 548 527 531
(1)用茎叶图表示两学生的成绩;
(2)分别求两学生成绩的中位数和平均分.
[命题意图]本题主要考查茎叶图、中位数和平均分以及考查学生对数据的处理能力.
[解析](1)两学生成绩绩的茎叶图如图所示 :……6分
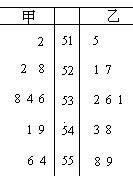 (2)将甲、乙两学生的成绩从小到大排列为:
(2)将甲、乙两学生的成绩从小到大排列为:
甲: 512 522 528 534 536 538 541 549 554 556
……7分
乙:515 521 527 531 532 536 543 548 558 559
……8分
从以上排列可知甲学生成绩的中位数为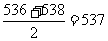 ……9分
……9分
乙学生成绩的中位数为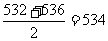 ……10分
……10分
甲学生成绩的平均数为:
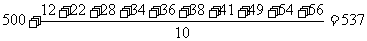 ……11分
……11分
乙学生成绩的平均数为:
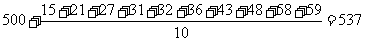 ……12分
……12分
6(汉沽一中2008~2009届月考文17)、(本小题满分14分)
某射手在一次射击中命中9环的概率是0.28,命中8环的概率是0.19,不够8环的概率是0.29,计算这个射手在一次射击中命中9环或10环(最高环数)的概率.
17[命题意图]本题主要考查互斥事件、对立事件、概率的基本性质以及考查学生用概念和公式规范解题的能力.
[解析]记这个射手在一次射击中“命中10环或9环”为事件A,“命中10环、9环、8环、不够8环”分别记为B、C、D、E. ……1分
则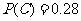 ,
,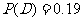 ,
,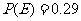 ……2分
……2分
∵C、D、E彼此互斥, ……3分
∴P(C∪D∪E)=P(C)+P(D)+P(E)=0.28+0.19+0.29=0.76. ……7分
又∵B与C∪D∪E为对立事件, ……8分
∴P(B)=1-P(C∪D∪E)=1-0.76=0.24. ……10分
B与C互斥,且A=B∪C, ……11分
∴P(A)=P(B+C)=P(B)+P(C) =0.24+0.28=0.52. ……13分
答:某射手在一次射击中命中9环或10环(最高环数)的概率为0.52. ……14分
7(汉沽一中2008~2008学年月考理15).(本小题满分13分)
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设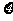 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且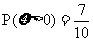 .
.
(I) 求文娱队的人数;
(II) 写出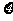 的概率分布列并计算
的概率分布列并计算 .
.
解:设既会唱歌又会跳舞的有x人,则文娱队中共有(7-x)人,那么只会一项的人数是
(7-2 x)人.
(I)∵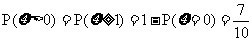 ,
,
∴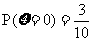 .……………………………………3分
.……………………………………3分
即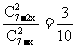 .
.
∴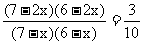 .
.
∴x=2. ……………………………………5分
故文娱队共有5人.……………………………………7分
(II)  的概率分布列为
的概率分布列为
 |
0 |
1 |
2 |
|
P |
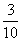 |
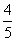 |
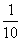 |
 ,……………………………………9分
,……………………………………9分
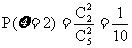 ,……………………………………11分
,……………………………………11分
∴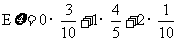 =1. …………………………13分
=1. …………………………13分
8(和平区2008年高考数学(文)三模18). (本小题满分12分)
有甲、乙、丙三种产品,每种产品的测试合格率分别为0.8,0.8和0.6,从三种产品中各抽取一件进行检验。
(1)求恰有两件合格的概率;
(2)求至少有两件不合格的概率。
解:(1)设从甲、乙、丙三种产品中各抽出一件测试为事件A,B,C,由已知P(A)=0.8,P(B)=0.8,P(C)=0.6
则恰有两件产品合格的概率为
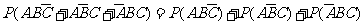
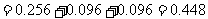 (6分)
(6分)
(2)三件产品均测试合格的概率为
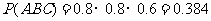 (8分)
(8分)
由(1)知,恰有一件测试不合格的概率为
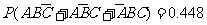 (10分)
(10分)
所以至少有两件不合格的概率为
 (12分)
(12分)
9(和平区2008年高考数学(理)三模18). (本小题满分12分)
有一批数量很大的产品,其次品率是10%。
(1)连续抽取两件产品,求两件产品均为正品的概率;
(2)对这批产品进行抽查,每次抽出一件,如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但抽查次数最多不超过4次,求抽查次数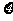 的分布列及期望。
的分布列及期望。
18. (本小题满分12分)
解:(1)两件产品均为正品的概率为
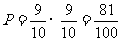 (3分)
(3分)
(2)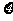 可能取值为1,2,3,4
可能取值为1,2,3,4
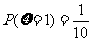 ;
;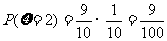 ;
;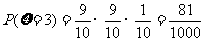
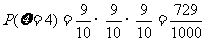 (9分)
(9分)
所以次数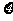 的分布列如下
的分布列如下
 (10分)
(10分)
∴ 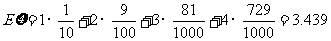 (12分)
(12分)
1(2009年滨海新区五所重点学校联考文14).某中学高中部有三个年级,其中高三有600人,采用分层抽样抽取一个容量为45的样本。已知高一年级抽取15人,高二年级抽取10人,则高中部的总人数是 1350
2(汉沽一中2008~2009届月考理10).某高三学生希望报名参加某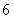 所高校中的
所高校中的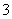 所学校的自主招生考试,由于其中两所学校的考试时间相同,因此,该学生不能同时报考这两所学校.则该学生不同的报名方法种数是
.(用数字作答) 16 .
所学校的自主招生考试,由于其中两所学校的考试时间相同,因此,该学生不能同时报考这两所学校.则该学生不同的报名方法种数是
.(用数字作答) 16 .
3(汉沽一中2008~2009届月考文11)、为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为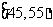 ,
,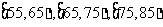 ,
,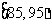 由此得到频率分布直方图如下图,则这20名工人中一天生产该产品数量在
由此得到频率分布直方图如下图,则这20名工人中一天生产该产品数量在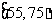 的人数是 .
的人数是 .
[答案]13
[命题意图]本题主要考查用样本的频率分布估计总体分布以及考查学生的识图能力.
[解析]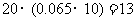
4(和平区2008年高考数学(文)三模11). 为了让人们感知塑料袋对环境造成的影响,某班环保小组的六名同学记录了自己家中一周内丢弃的塑料袋的数量,结果如下(单位:个):33,25,28,26,25,31,如果该班45名学生。那么根据提供的数据,估计本周全班同学各家丢弃塑料袋的总数量约为 。1260
5(2009年滨海新区五所重点学校联考理16).给定下列结论:
①在区间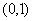 内随机地抽取两数
内随机地抽取两数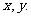 则满足
则满足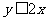 概率是
概率是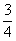 ;
;
②已知直线l1: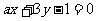 ,l2:x- by + 1= 0,则
,l2:x- by + 1= 0,则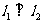 的充要条件是
的充要条件是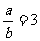 ;
;
 ③为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)。根据所得数据画出样本的频率分布直方图(如右),那么在这100株树木中,底部周长小于110cm的株数是70株;
③为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)。根据所得数据画出样本的频率分布直方图(如右),那么在这100株树木中,底部周长小于110cm的株数是70株;
④极坐标系内曲线 的中心
的中心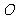 与点
与点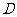
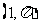 的距离为
的距离为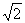 .
.
以上结论中正确的是_____________________(用序号作答) 16. ①③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com