
10、应用导数解函数的单调性问题:(1)、若f′(x)>0,则f(x)为增函数,
(2)、若f′(x)<0,则f(x)为减函数,
(3)、若f′(x)=0恒成立,则f(x)为常数函数,
(4)、若f′(x)的符号不确定,则f(x)不量单调函数,
(5)、利用导数法来划分函数的单调区间时,单调增区间,Û f′(x)³0且等号不恒成立。
单调减区间,Û f′(x)£0且等号不恒成立。可利用下列步骤来划分区间:
1)求f′(x),2)求方程f′(x)=0的根,设根为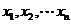 ,3)
,3)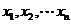 将给定区间分成n+1个子区间,再在每一个子区间内判断f′(x)的符号。4)对于方程f′(x)=0无意义的点也要考虑。应用单调性求参数的取值范围时,注意f/(x)=0的点; 如:设
将给定区间分成n+1个子区间,再在每一个子区间内判断f′(x)的符号。4)对于方程f′(x)=0无意义的点也要考虑。应用单调性求参数的取值范围时,注意f/(x)=0的点; 如:设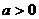 函数
函数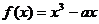 在
在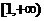 上单调函数,则实数
上单调函数,则实数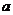 的取值范围______(答:
的取值范围______(答: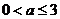 );
);
9、应用导数解有关切线问题:过某点的切线不一定只有一条; 如:已知函数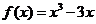 过点
过点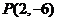 作曲线
作曲线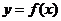 的切线,求此切线的方程
的切线,求此切线的方程
(答:切点分别为(0,0),(3,18)。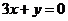 或
或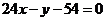 )。
)。
解这类题首先要弄清楚已知点是否为切点,如果不是切点,应先设切点为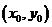 然后写出切线方程:
然后写出切线方程: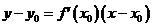 再把已知点代入求出切点。如果已知点是切点,则直线求此点的导数得出直线的斜率。
再把已知点代入求出切点。如果已知点是切点,则直线求此点的导数得出直线的斜率。
8、导数的运算法则: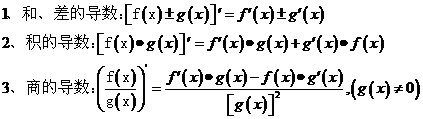
复合函数的导数:首先要弄清复合函数的复合关系。它的求导法则是:复合函数对自变量的导数,等于已知函数对中间变量的导数乘以中间变量对自变量的导数,即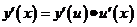
7、几种常见函数的导数:(1)、常函数的导数为0,即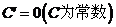 ,
,
(2)、幂函数的导数为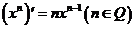 ,与此有关的如下:
,与此有关的如下:
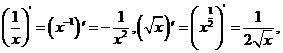
(3)、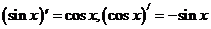 ,
,
(4)、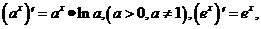
(5)、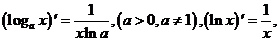
6、导数的几何意义:函数f(x)在点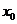 处的导数的几何意义,就是曲线y=f(x)在点
处的导数的几何意义,就是曲线y=f(x)在点
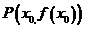 处的切线的斜率,即曲线y=f(x)在点
处的切线的斜率,即曲线y=f(x)在点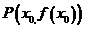 处的切线的斜率是
处的切线的斜率是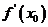 ,相应地切线的方程是
,相应地切线的方程是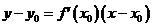
5、如果函数f(x)在点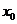 处可导,那么函数f(x)在点
处可导,那么函数f(x)在点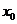 处连续,反之不一定成立。如:y=
处连续,反之不一定成立。如:y=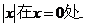 连续不可导。
连续不可导。
4、导函数的概念:如果函数f(x)在开区间(a,b)内可导,对于开区间(a,b)内的每一个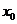 ,都对应着一个导数
,都对应着一个导数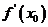 ,这样f(x)在开区间(a,b)内构成一个新的函数,这一新的函数叫做f(x)在开区间(a,b)内的导函数,记作
,这样f(x)在开区间(a,b)内构成一个新的函数,这一新的函数叫做f(x)在开区间(a,b)内的导函数,记作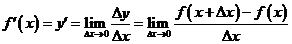 ,导函数也简称为导数。
,导函数也简称为导数。
3、导数的概念:
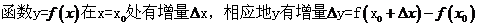
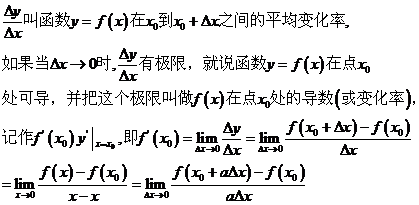
2、瞬时速度: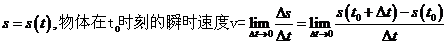
1、曲线的切线:设曲线C是函数y=f(x)的图象,在曲线C上取一点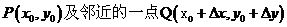 ,过P,Q两点作割线,当点Q沿着曲线逐渐向点P接近时,即
,过P,Q两点作割线,当点Q沿着曲线逐渐向点P接近时,即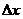 →0时,割线PQ的极限位置PT,直线PT叫做曲线在点P处的切线。设切线PT的倾斜角为
→0时,割线PQ的极限位置PT,直线PT叫做曲线在点P处的切线。设切线PT的倾斜角为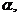 割线PQ的斜率的极限就是曲线C在点P处的切线的斜率,
割线PQ的斜率的极限就是曲线C在点P处的切线的斜率,
即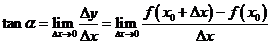
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com