
1、 数的分类:
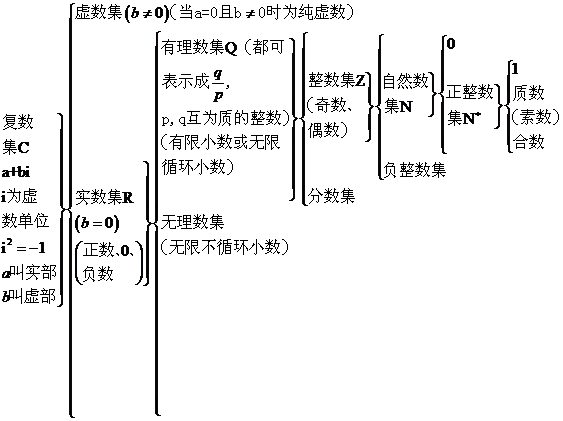
6、 归纳法分为不完全归纳法和完全归纳法。数学归纳法:是证明与自然数集有关的命题,它是在归纳的基础上进行的演绎推理,所得结论一般是正确的。是不完全归纳法的一种。
数学归纳法的一般步骤是:(1)验证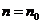 时,结论正确,
时,结论正确,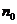 是使命题成立的最自然数。(2)假设当
是使命题成立的最自然数。(2)假设当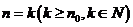 时命题成立,证明当
时命题成立,证明当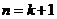 时命题也成立,(3)作结论,由(1)(2)知命题成立。
时命题也成立,(3)作结论,由(1)(2)知命题成立。
第二十二讲数系的扩充与复数的引入
5、 反证法:假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立。这种方法叫反证法,它是间接证明的基本方法。反证法的一般步骤是:(1)反设:假设所要证明的结论不成立即结论的反面成立,(2)归谬:由“反设”出发,通过正确的推理,导出矛盾___与已知条件、已知公理、定义、定理、反设及明显的事实矛盾。(3)结论:肯定原命题成立。
宜用反证法的题型有:(1)一些基本命题,一些基本定理,(2):“否定性”命题,(3)“惟一性”命题,(4)“至多”“至少”类命题,(5)涉及“无限”结论的命题。
4、 分析法:从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止。又叫逆推证法或执因索果法。
3、 综合法:利用已知条件和某些数学定义、公理、定理等,经过一系的推理论证,最后推导出所要证明的结论成立。又叫由因导果法或顺推证法。
2、 演绎推理:从一般性的原理,推出某个特殊情况下的结论。是从一般到特殊的推理。“三段论”是演绎推理的一般模式,它包括:(1)大前提___已知的一般原理。(2)小前提___所研究的特殊情况。(3)结论__根据一般原理对特殊情况做出的判断。演绎推理是一个必然性的推理,演绎推理产前提与结论之间有蕴涵关系,只要大前提、小前提都是真实的,推理的形式是正确的,那么结论必是真实的。但错误的前提可能导致错误的结论,推理的形式不对也会导致错误的结论。
1、 合情推理最常见的是归纳和类比。由某类事物的部分对象具有某些特征推出该类事物的全部对象具有这些特征的推理。或者由个别事实概括出一般结论的推理,称为归纳推理,简言之是从部分到整体,从个别到一般的推理。由两类对象具有某些类似特征和其中一类对象具有的某些已知特征推出另一类对象也具有这些特征的推理称为类比推理。类比推理是从特殊到特殊的推理。
练习:(1)、观察下图中各正方形图案,每条边上有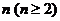 个圆圈,每个图案中圆圈的总数是
个圆圈,每个图案中圆圈的总数是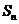 ,按此规律推出:当
,按此规律推出:当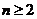 时,
时,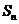 与
与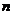 的关系式 .key:
的关系式 .key: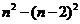
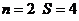
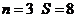
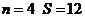
(2)、观察下式:1=12,2+3+4=32,3+4+5+6+7=52,4+5+6+7+8+9+10=72,…,则可得出一般结论: . key:
key: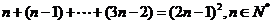
(3)类比平面内的直角三角形的性质猜想空间中的类似定理。
13、定积分:(1).直线
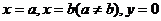 和直线y=f(x)所围成的图形称为曲边梯形。
和直线y=f(x)所围成的图形称为曲边梯形。
(2). 定积分概念:设函数f(x)在区间[a,b]上连续,用分点a=x0<x1<…<xi-1<xi<…xn=b把区间[a,b]等分成n个小区间,在每个小区间[xi-1,xi]上取任一点ξi(i=1,2,…n)作和式In=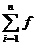 (ξi)△x(其中△x为小区间长度),把n→∞即△x→0时,和式In的极限叫做函数f(x)在区间[a,b]上的定积分。记作:
(ξi)△x(其中△x为小区间长度),把n→∞即△x→0时,和式In的极限叫做函数f(x)在区间[a,b]上的定积分。记作: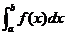 ,即
,即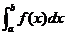 =
=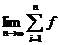 (ξi)△x。
(ξi)△x。
这里,a与b分别叫做定积分的下限与上限。区间[a,b]叫做积分区间,函数f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式。
(3).定积分的性质:
①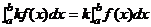 (k为常数);
(k为常数);
②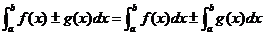 ;
;
③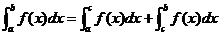 (其中a<c<b
(其中a<c<b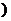 。
。
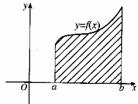
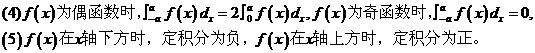 当位于x轴上方的曲边梯形的面积等于位于x轴下方的曲边梯形的面积时,定积分的值为0。
当位于x轴上方的曲边梯形的面积等于位于x轴下方的曲边梯形的面积时,定积分的值为0。
(4)定积分的计算:如果f(x)是区间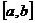 上的连续函数,并且
上的连续函数,并且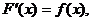 那么
那么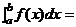 F(b)-F(a)。这个结论叫做微积分基本定理。又叫莱面尼兹公式。
F(b)-F(a)。这个结论叫做微积分基本定理。又叫莱面尼兹公式。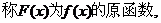
为了方便,我们常常把F(b)-F(a)记成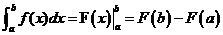
(5).定积分求曲边梯形面积
由三条直线x=a,x=b(a<b),x轴及一条曲线y=f(x)围成的曲边梯的面积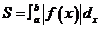
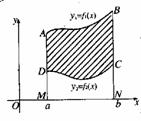 如果图形由曲线y1=f1(x),y2=f2(x),及直线x=a,x=b(a<b)围成,那么所求图形的面积
如果图形由曲线y1=f1(x),y2=f2(x),及直线x=a,x=b(a<b)围成,那么所求图形的面积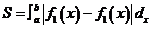
.在利用定积分求平面图形的面积时,一般要先画出它的草图,通过解方程组确定相应的积分区间。
(6)定积分的物理应用:.物体做变速直线运动经过的位移s等于其速度函数v=v(t)在时间区间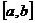 上的定积分
上的定积分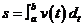 。
。
如果物体沿与变力F(x)相同的方向移动,那么从位置x=a到x=b变力所做的功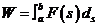
第二十一讲推理与证明
12、应用导数解函数的最大值和最小值问题:
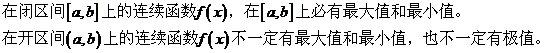 求极值、最值步骤:求导数;求
求极值、最值步骤:求导数;求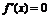 的根;检验
的根;检验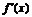 在根左右两侧符号,若左正右负,则f(x)在该根处取极大值;若左负右正,则f(x)在该根处取极小值;把极值与区间端点函数值比较,最大的为最大值,最小的是最小值. 如:(1)函数
在根左右两侧符号,若左正右负,则f(x)在该根处取极大值;若左负右正,则f(x)在该根处取极小值;把极值与区间端点函数值比较,最大的为最大值,最小的是最小值. 如:(1)函数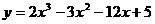 在[0,3]上的最大值、最小值分别是______(答:5;
在[0,3]上的最大值、最小值分别是______(答:5;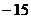 );(2)已知函数
);(2)已知函数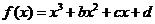 在区间[-1,2
]上是减函数,那么b+c有最__值__答:大,
在区间[-1,2
]上是减函数,那么b+c有最__值__答:大,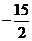 )(3)方程
)(3)方程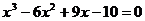 的实根的个数为__(答:1)
的实根的个数为__(答:1)
特别提醒:(1)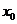 是极值点的充要条件是
是极值点的充要条件是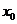 点两侧导数异号,而不仅是
点两侧导数异号,而不仅是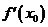 =0,
=0,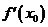 =0是
=0是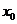 为极值点的必要而不充分条件。(2)给出函数极大(小)值的条件,一定要既考虑
为极值点的必要而不充分条件。(2)给出函数极大(小)值的条件,一定要既考虑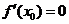 ,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记!如:函数
,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记!如:函数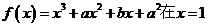 处有极小值10,则a+b的值为____(答:-7)
处有极小值10,则a+b的值为____(答:-7)
11、应用导数解函数的极值问题:(1)、设函数f(x)在点x 附近有定义,如果对x
附近有定义,如果对x 附近所有的点,都有f(x)<f(x
附近所有的点,都有f(x)<f(x ),就说是f(x
),就说是f(x )函数f(x)的一个极大值。记作
)函数f(x)的一个极大值。记作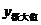 =f(x
=f(x ),如果对x
),如果对x 附近所有的点,都有f(x)>f(x
附近所有的点,都有f(x)>f(x ),就说是f(x
),就说是f(x )函数f(x)的一个极小值。记作
)函数f(x)的一个极小值。记作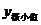 =f(x
=f(x ),极大值和极小值统称为极值。
),极大值和极小值统称为极值。
(2)、当函数f(x)在点x 处连续时,(1)如果在点x
处连续时,(1)如果在点x 附近左侧
附近左侧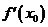 >0,右侧
>0,右侧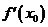 <0,则f(x
<0,则f(x )是极大值,x
)是极大值,x 是极大值点。(2)如果在点x
是极大值点。(2)如果在点x 附近左侧
附近左侧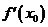 <0,右侧
<0,右侧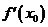 >0,则f(x
>0,则f(x )是极小值,x
)是极小值,x 是极小值点。(3)x
是极小值点。(3)x 是极值点的充要条件是x
是极值点的充要条件是x 点两侧导数异号,而不仅是
点两侧导数异号,而不仅是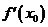 =0,
=0,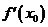 =0是x
=0是x 为极值点的既不必要而不充分条件。
为极值点的既不必要而不充分条件。
如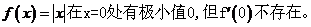 但对可导函数
但对可导函数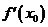 =0是x
=0是x 为极值点的必要而不充分条件。
为极值点的必要而不充分条件。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com