3、更为一般的情况是：设是定义在区间[a,b]上的函数，如果对于[a,b]上的任意两点，有

其中，则称是区间[a,b]上的凸函数。如果不等式反向，即有则称是[a,b]上的凹函数。

2、其推广形式是：若函数的是[a,b]上的凸函数，则对[a,b]内的任意数，都有

　　　　 　　　(2)

当且仅当时等号成立。一般称(2)式为琴生不等式。　　

1、设函数的定义域为[a,b]，如果对于[a,b]内任意两数，都有

　　　　 　　　　　(1)

则称为[a,b]上的凸函数。若把(1)式的不等号反向，则称这样的为[a,b]上的凹函数。凸函数的几何意义是：过曲线上任意两点作弦，则弦的中点必在该曲线的上方或在曲线上。

②．基本不等式：　　 ≥()　

语言表述：n个正数的算术平均数不小于它们的几何平均数。

③．的几何解释：

以为直径作圆，在直径AB上取一点C，过C作弦DD’^AB　 则，

从而，而半径。

一般地，设有两组实数：，，，…，与，，，…，，且它们满足：

≤≤≤…≤，≤≤≤…≤，

若，，，…，是，，，…，的任意一个排列，则和数在，，，…，与，，，…，同序时最大，反序时最小，即：

，

等号当且仅当或时成立。

4、定理4：(柯西不等式的推广形式)：设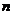为大于1的自然数，(1，2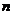，…，)为任意实数，则：，其中等号当且仅当时成立(当时，约定，1，2，…，)。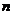

证明：构造二次函数：

　　 即构造了一个二次函数：

由于对任意实数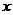，恒成立，则其，

即：，

即：，

等号当且仅当，

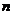即等号当且仅当时成立(当时，约定，1，2，…，)。如果()全为0，结论显然成立。

柯西不等式有两个很好的变式：

变式1 设 ，等号成立当且仅当

变式2 　设a_i，b_i同号且不为0(i=1，2，…，n)，则：，等号成立当且仅当。

3、定理3：(三角形不等式)设为任意实数，则：

思考：三角形不等式中等号成立的条件是什么？

，

　　　　　　 其中等号当且仅当时成立。

几何意义：设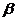，为平面上以原点O为起点的两个非零向量，它们的终点分别为A()，B()，那么它们的数量积为，

而，，

所以柯西不等式的几何意义就是：，

其中等号当且仅当两个向量方向相同或相反(即两个向量共线)时成立。

2、定理2：(柯西不等式的向量形式)设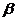，为平面上的两个向量，则，其中等号当且仅当两个向量方向相同或相反(即两个向量共线)时成立。

12. 常见曲线的参数方程的一般形式：

　　 (1)经过点P₀(x₀，y₀)，倾斜角为a的直线的参数方程为

称为直线的标准参数方程。

经过点P₀(x₀，y₀)，以为方向向量的直线的参数方程为

称为直线的一般参数方程。

此式中的。

　　 利用直线的参数方程，研究直线与圆锥曲线的位置关系以及弦长计算，有时比较方便。方法是：

　　 则(1)当△<0时，l与C无交点；(2)当△=0时，l与C有一公共点；(3)当△>0时，l与C有两个公共点；此时方程at²+bt+c=0有两个不同的实根t₁、t₂，把参数t₁、t₂代入l的参数方程，即可求得l与C的两个交点M₁、M₂的坐标；另外，由参数t的几何

(2)　　　 圆、椭圆、双曲线、抛物线的参数方程

(3)摆线：

当一个圆沿着一条定直线无滑动地滚动时，圆周上一个定点P的轨迹是什么？

我们把定点P的轨迹叫做平摆线，又叫旋轮线。

(4)圆的渐开线：

第二七讲不等式选讲

11、 化普通方程为参数方程的基本思路是引入参数，即选定合适的参数t，先确定一个关系x=f(t)(或y=j(t))，再代入普通方程F(x，y)＝0，求得另一关系y=j(t)(或x=f(t))。一般地，常选择的参数有角(如圆、椭圆、双曲线)、有向线段的数量(如直线)、斜率(抛物线是以斜率的倒数为参数)，某一点的横坐标(或纵坐标)。