
12.三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那麽它也和这条斜线的射影垂直 推理模式:
推理模式:
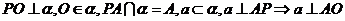 .
.
注意:⑴三垂线指PA,PO,AO都垂直α内的直线a 其实质是:斜线和平面内一条直线垂直的判定和性质定理
其实质是:斜线和平面内一条直线垂直的判定和性质定理 ⑵要考虑a的位置,并注意两定理交替使用
⑵要考虑a的位置,并注意两定理交替使用
基本题型:
10.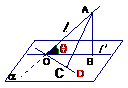 直线和平面所成角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角
直线和平面所成角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角 一直线垂直于平面,所成的角是直角
一直线垂直于平面,所成的角是直角
一直线平行于平面或在平面内,所成角为0°角。直线和平面所成角范围: [0,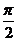 ]
]
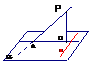 (2)定理:斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角
(2)定理:斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角
11  三垂线定理 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直
三垂线定理 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直
说明:(1)定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系;
(2)推理模式: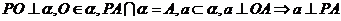

9.射影长相等定理:从平面外一点向这个平面所引的垂线段和斜线中⑴射影相交两条斜线相交;射影较长的斜线段也较长 ⑵相等的斜线段射影相等,较长的斜线段射影较长;⑶垂线段比任何一条斜线段都短
⑵相等的斜线段射影相等,较长的斜线段射影较长;⑶垂线段比任何一条斜线段都短
7.平面几何中,点、线段在直线上射影的概念及性质:
8  斜线,垂线,射影
斜线,垂线,射影
⑴垂线 自一点向平面引垂线,垂足叫这点在这个平面上的射影. 这个点和垂足间的线段叫做这点到这个平面的垂线段.
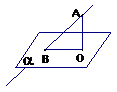 ⑵斜线 一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线
⑵斜线 一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线 斜线和平面的交点叫斜足;斜线上一点与斜足间的线段叫这点到这个平面的斜线段
斜线和平面的交点叫斜足;斜线上一点与斜足间的线段叫这点到这个平面的斜线段
⑶射影 过斜线上斜足外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影 垂足和斜足间线段叫这点到这个平面的斜线段在这个平面内的射影
垂足和斜足间线段叫这点到这个平面的斜线段在这个平面内的射影
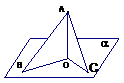 直线与平面平行,直线在平面由射影是一条直线
直线与平面平行,直线在平面由射影是一条直线 直线与平面垂直射影是点
直线与平面垂直射影是点 斜线任一点在平面内的射影一定在斜线的射影上
斜线任一点在平面内的射影一定在斜线的射影上
17. 正四面体ABCD的棱长为a,球O是内切球,球O1是与正四面体的三个面和球O都相切的一个小球,求球O1的体积.
16.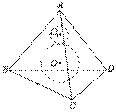 表面积为
表面积为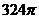 的球,其内接正四棱柱的高是
的球,其内接正四棱柱的高是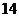 ,求这个正四棱柱的表面积
,求这个正四棱柱的表面积
14.正方体全面积是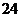 ,它的外接球的体积是 ,内切球的体积是
.
,它的外接球的体积是 ,内切球的体积是
.
15 ?球O1、O2分别与正方体的各面、各条棱相切,正方体的各顶点都在球O3的表面上,求三个球的表面积之比.
?球O1、O2分别与正方体的各面、各条棱相切,正方体的各顶点都在球O3的表面上,求三个球的表面积之比.
13.把半径分别为3,4,5的三个铁球,熔成一个大球,则大球半径是 ;
12.若球的大圆面积扩大为原来的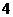 倍,则球的体积比原来增加 倍;
倍,则球的体积比原来增加 倍;
11.三个球的半径之比为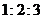 ,那么最大的球的体积是其余两个球的体积和的 倍;
,那么最大的球的体积是其余两个球的体积和的 倍;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com