
20.(14分)已知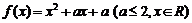 ,
,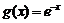 ,
,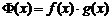 .
.
(1)当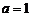 时,求
时,求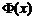 的单调区间;
的单调区间;
(2)求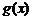 在点
在点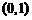 处的切线与直线
处的切线与直线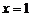 及曲线
及曲线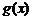 所围成的封闭图形的面积;
所围成的封闭图形的面积;
(3)是否存在实数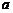 ,使
,使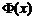 的极大值为3?若存在,求出
的极大值为3?若存在,求出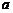 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
18.(14分) 已知圆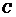 方程为:
方程为: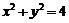 .
.
(1)直线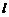 过点
过点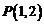 ,且与圆
,且与圆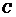 交于
交于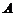 、
、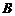 两点,若
两点,若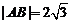 ,求直线
,求直线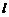 的方程;
的方程;
(2)过圆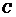 上一动点
上一动点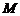 作平行于
作平行于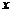 轴的直线
轴的直线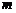 ,设
,设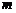 与
与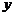 轴的交点为
轴的交点为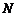 ,若向量
,若向量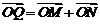 ,求动点
,求动点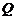 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
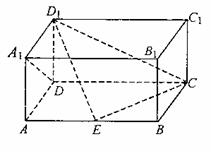 19.(14分)如图,在长方体
19.(14分)如图,在长方体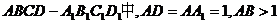 ,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为
,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为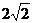 .
.
(1)求证:D1E⊥A1D;
(2)求AB的长度;
(3)在线段AB上是否存在点E,使得二面角
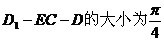 。若存在,确定
。若存在,确定
点E的位置;若不存在,请说明理由.
17. (12分)某公司有10万元资金用于投资,如果投资甲项目,根据市场分析知道:一年后可能获利10﹪,可能损失10﹪,可能不赔不赚,这三种情况发生的概率分别为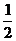 ,
,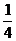 ,
,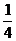 ;如果投资乙项目,一年后可能获利20﹪,也可能损失20﹪,这两种情况发生的概率分别为
;如果投资乙项目,一年后可能获利20﹪,也可能损失20﹪,这两种情况发生的概率分别为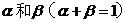 .
.
(1)如果把10万元投资甲项目,用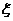 表示投资收益(收益=回收资金-投资资金),求
表示投资收益(收益=回收资金-投资资金),求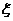 的概率分布及
的概率分布及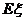 ;
;
(2)若把10万元投资投资乙项目的平均收益不低于投资甲项目的平均收益,求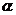 的取值范围.
的取值范围.
16. (12分)设函数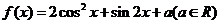 .
.
(1)求函数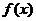 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当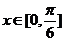 时,
时,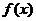 的最大值为2,求
的最大值为2,求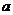 的值,并求出
的值,并求出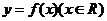 的对称轴方程.
的对称轴方程.
(二)选做题(13--15题,考生只能从中选作2题)
13.(坐标系与参数方程选做题) (坐标系与参数方程选做题)两直线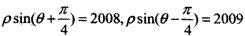 的位置关系是______(判断垂直或平行或斜交)
的位置关系是______(判断垂直或平行或斜交)
14. (不等式选讲选做题)
不等式
(不等式选讲选做题)
不等式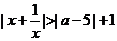 对于一非零实数x均成立,则实数a的取值范围是_________
对于一非零实数x均成立,则实数a的取值范围是_________
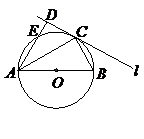
15.(几何证明选讲选做题) 如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线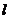 ,则点A到直线
,则点A到直线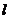 的距离AD为 .
的距离AD为 .
(一)必做题(9--12题)
9.在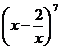 的展开式中,
的展开式中,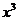 的系数是
.(用数字作答)
的系数是
.(用数字作答)
10. 一个均匀小正方体的六个面中,三个面上标以数0,两个面上标以数1,一个面上标以数2,将这个小正方体抛掷2次,则向上的数之积为0的概率
.
一个均匀小正方体的六个面中,三个面上标以数0,两个面上标以数1,一个面上标以数2,将这个小正方体抛掷2次,则向上的数之积为0的概率
.
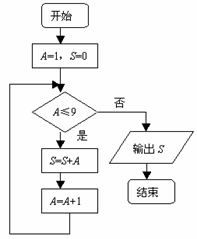
11.如图,该程序运行后输出的结果为 .
12.已知点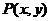 满足条件
满足条件
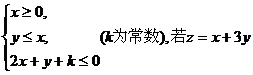 的最大值为8,
的最大值为8,
则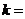 .
.
8.已知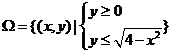 ,直线
,直线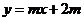 和曲线
和曲线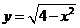 有两个不同的交点,它们围成的平面区域为
有两个不同的交点,它们围成的平面区域为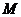 ,向区域
,向区域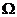 上随机投一点A,点A落在区域
上随机投一点A,点A落在区域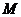 内的概率为
内的概率为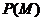 ,若
,若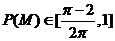 ,则实数
,则实数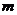 的取值范围为
的取值范围为
A.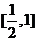 B.
B.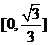 C.
C.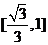 D.
D. 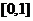
7.两个正数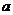 、
、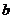 的等差中项是
的等差中项是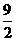 ,一个等比中项是
,一个等比中项是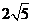 ,且
,且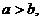 则双曲线
则双曲线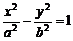 的离心率为
的离心率为
A.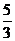 B.
B.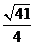 C.
C.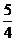 D.
D.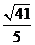
6.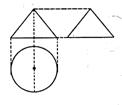 如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么几何体的侧面积为
如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么几何体的侧面积为
A. 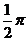 B.
B. 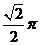
C. 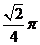 D.
D.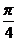
5.已知函数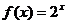 的反函数
的反函数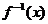 满足
满足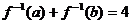 ,则
,则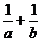 的最小值为
的最小值为
A.1 B.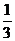 C.
C.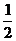 D.
D.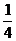
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com