
8.设奇函数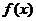 在
在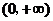 上为增函数,且
上为增函数,且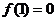 ,则不等式
,则不等式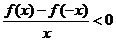 的解集为( )
的解集为( )
A.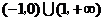 B.
B.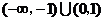
C.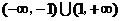 D.
D.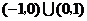
7.已知函数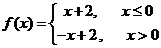 ,则不等式
,则不等式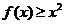 的解集是( )
的解集是( )
(A)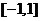 (B)
(B)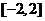 (C)
(C)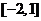 (D)
(D)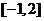
6.若点P(2,0)到双曲线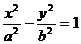 的一条渐线的距离为
的一条渐线的距离为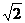 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
(A)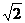 (B)
(B)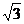 (C)
(C)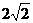 (D)
(D)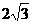
5.复数 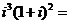 ( )
( )
A.2 B.-2 C. 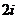 D.
D. 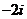
4.已知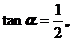 ,则
,则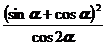 = ( )
= ( )
(A)2 (B)-2 (C)3 (D)-3
3.函数f(x)=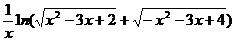 的定义域为
的定义域为
A.(- ∞,-4)[∪2,+ ∞] B.(-4,0) ∪(0,1)
C. [-4,0]∪(0,1)] D. [-4,0∪(0,1)
2.用与球心距离为1的平面去截球,所得的截面面积为π,则球的休积为
A.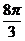 B.
B. 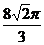 C.
C.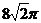 D.
D. 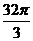
1.若非空集合A,B,C满足A∪B=C,且B不是A的子集,则
A.“x∈C”是“x∈A”的充分条件但不是必要条件
B. “x∈C”是“x∈A”的必要条件但不是充分条件
C. “x∈C”是“x∈A”的充分条件
D. “x∈C”是“x∈A”的充分条件也不是“x∈A”必要条件
21.(本题满分14分)
已知数列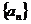 中,
中,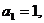 且点
且点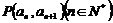 在直线
在直线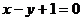 上.
上.
(1)求数列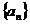 的通项公式;
的通项公式;
(2)若函数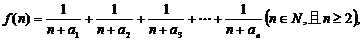 求函数
求函数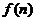 的最小值;
的最小值;
(3)设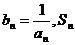 表示数列
表示数列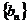 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于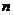 的整式
的整式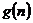 ,使得
,使得
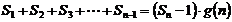 对于一切不小于2的自然数
对于一切不小于2的自然数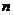 恒成立?
若存在,写出
恒成立?
若存在,写出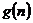 的解析式,并加以证明;若不存在,试说明理由.(东莞市2009届高三模拟试题(二))
的解析式,并加以证明;若不存在,试说明理由.(东莞市2009届高三模拟试题(二))
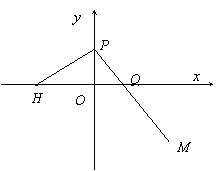
20、(14分)已知点H(-3,0),点P在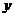 轴上,点Q在
轴上,点Q在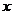 轴的正半轴上,点M在直线PQ上,且满足
轴的正半轴上,点M在直线PQ上,且满足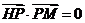 ,
, 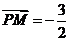
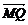 .
.
(Ⅰ)当点P在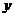 轴上移动时,求点M的轨迹C;
轴上移动时,求点M的轨迹C;
(Ⅱ)过定点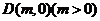 作直线
作直线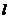 交轨迹C于A、B两点,E是D点关于坐标原点O的对称点,求证:
交轨迹C于A、B两点,E是D点关于坐标原点O的对称点,求证: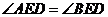 ;
;
 (Ⅲ)在(Ⅱ)中,是否存在垂直于
(Ⅲ)在(Ⅱ)中,是否存在垂直于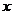 轴的直线
轴的直线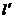 被以AD为直径的圆截得的弦长恒为定值?若存在求出
被以AD为直径的圆截得的弦长恒为定值?若存在求出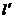 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com