
5.(福建省莆田四中2008届5月份第二次模拟考试,理科,21)
已知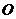 为坐标原点,点
为坐标原点,点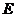 、
、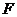 的坐标分别为
的坐标分别为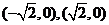 ,点
,点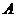 、
、 满足
满足
|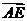 |
|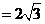 ,
,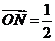 (
(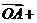
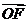 ),过点
),过点 且垂直于
且垂直于 的直线交线段
的直线交线段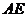 于点
于点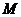 ,
,
设点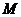 的轨迹为
的轨迹为 .
.
(1)求轨迹 的方程;
的方程;
(2)设直线的 :
: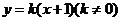 与轨迹
与轨迹 交于不同的两点
交于不同的两点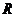 、
、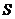 ,对点
,对点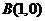 和向量
和向量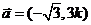 ,求
,求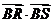
 取最大值时直线
取最大值时直线 的方程.
的方程.
[解析](1)由椭圆的定义易得点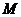 的轨迹
的轨迹 的方程;(2)设出
的方程;(2)设出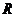 、
、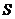 两点的坐标后转化成向量的坐标运算,进而由不等式放缩得到
两点的坐标后转化成向量的坐标运算,进而由不等式放缩得到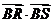
 取最大值时k的值,即得到直线
取最大值时k的值,即得到直线 的方程.
的方程.
[答案](1)∵=(+),∴N为AF的中点
∴||=||∴||+||=||+||>||
∴点M的轨迹C是以E、F为焦点的椭圆
∵长半轴a=,半焦距c=
∴b2=a2-c2=1
∴点M的轨迹C的方程为+y2=1
(2)将y=k(x+1)(k≠0)代入椭圆C:+y2=1中,整理得
(1+3k2)x2+6k2x+3k2-3=0
设R(x3,y3)、S(x4,y4)
则x3+x4=-,x3x4=
所以y3y4=k2(x3+1)(x4+1)=k2(x3+x4+x3x4+1)=-
∴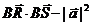 =(x3-1)(x4-1)+y3y4-3-9k2
=(x3-1)(x4-1)+y3y4-3-9k2
=x3x4-(x3+x4)+1+y3y4-3-9k2=++1--3-9k2
=-3-9k2=-[+3(1+3k2)]≤-2×4=-
当且仅当=3(1+3k2),即k2=∈(0,1)时等号成立
此时,直线l的方程为y=±(x+1)
4.(广东省实验中学2008届高三第三次模拟考试,理科,20)
已知抛物线x2=-y,直线L:(m+1)y+(3-m)x+m+1=0 (m∈R且m≠-1)与抛物线交于A,B两
点.
(1) 当m=0时,试用x,y的不等式组表示由直线L和抛物线围成的封闭图形所在平面区域(包边界) ,并求该区域的面积.
(2)求证:对任意不为零的实数m,抛物线的顶点都在以线段AB为直径的圆C上;并求圆
C的圆心的轨迹方程.
(3)将抛物线x2=-y的图像按向量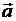 =(4,16)移动后得到函数y=f(x)的图像,若
=(4,16)移动后得到函数y=f(x)的图像,若
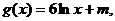 问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
[解析](1)所要表示的平面区域包括边界,要注意不等式取等号,由定积分即可求出相应
的面积,计算时可以整体代入;
(2)证明抛物线的顶点在以线段AB为直径的圆C上,即证明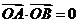 ,圆C的圆心的
,圆C的圆心的
轨迹可由中点坐标公式利用“代入法”求得;
(3)构造函数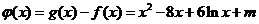 ,因为
,因为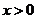 ,所以y=f(x)的图
,所以y=f(x)的图
象与y=g(x)的图象有且只有两个不同的交点问题就可以转化为函数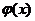 有两个正零点的
有两个正零点的
问题,要对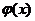 的单调性进行讨论,从而求出使得
的单调性进行讨论,从而求出使得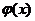 由两个正零点的
由两个正零点的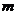 的取值范围.
的取值范围.
[答案]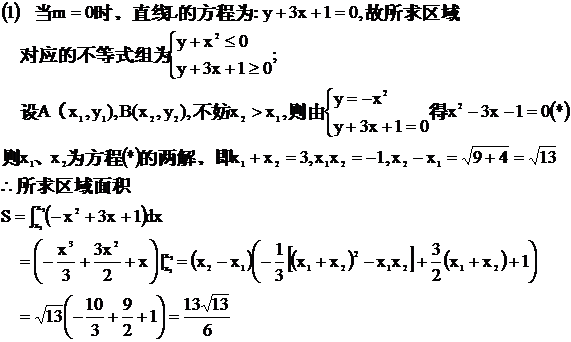
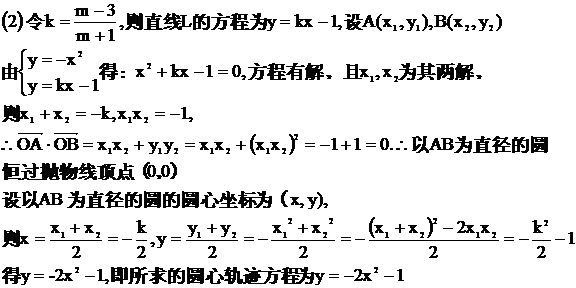 (3)依题意,f(x)=-x2+8x,令
(3)依题意,f(x)=-x2+8x,令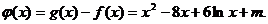
因为x>0,要使函数f(x)与函数g(x)有且仅有2个不同的交点,则函数
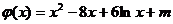 的图象与x轴的正半轴有且只有两个不同的交点
的图象与x轴的正半轴有且只有两个不同的交点
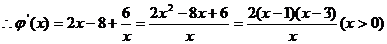
当x∈(0,1)时,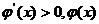 是增函数;
是增函数;
当x∈(1,3)时,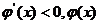 是减函数
是减函数
当x∈(3,+∞)时,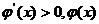 是增函数
是增函数
当x=1或x=3时,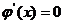
∴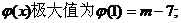
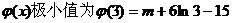
又因为当x→0时,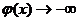
当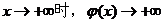
所以要使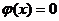 有且仅有两个不同的正根,必须且只须
有且仅有两个不同的正根,必须且只须
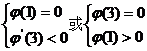
即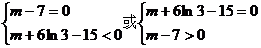
∴m=7或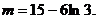
∴当m=7或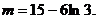 时,函数f(x)与g(x)的图象有且只有两个不同交点.
时,函数f(x)与g(x)的图象有且只有两个不同交点.
3.(宁夏银川一中2008届高三年级第五次月考测试,理科,21)
已知直线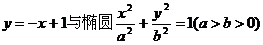 相交于A、B两点.
相交于A、B两点.
(1)若椭圆的离心率为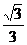 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(2)若向量 互相垂直(其中O为坐标原点),当椭圆的离心率
互相垂直(其中O为坐标原点),当椭圆的离心率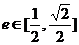
时,求椭圆的长轴长的最大值.
[解析](1)由已知条件易求椭圆的标准方程,再由弦长公式即可求得线段AB的长;(2)由向量 互相垂直可以设
互相垂直可以设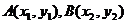 从而转化成坐标运算,求出
从而转化成坐标运算,求出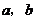 的关系,进而用离心率
的关系,进而用离心率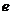 表示
表示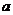 ,再由
,再由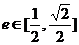 ,求出
,求出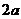 的范围即求出长轴长的最大值.
的范围即求出长轴长的最大值.
[答案](1)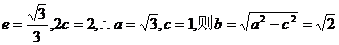 ,
,
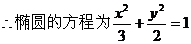 ,
,
联立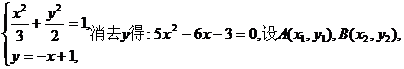
则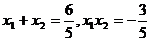
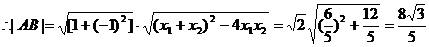 ,
,
(2)设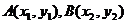 ,
,
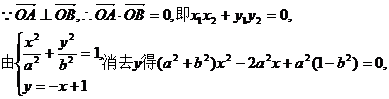
由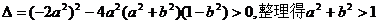 ,
,
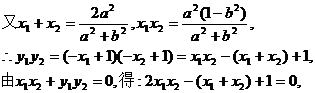
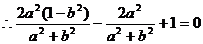 ,
,
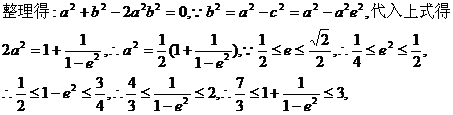
 ,
,
由此得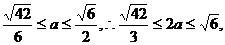
故长轴长的最大值为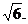
2.(山东省烟台市2008届高三5月适应性练习,理科,21)
如图,在平面直角坐标系中,N为圆A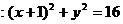 上的一动点,点B(1,0),点M
上的一动点,点B(1,0),点M
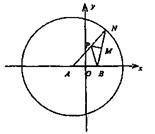 是BN中点,点P在线段AN上,且
是BN中点,点P在线段AN上,且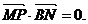
(1)求动点P的轨迹方程;
(2)试判断以PB为直径的圆与圆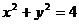 的位置关系,并说明理由。
的位置关系,并说明理由。
[解析](1)由垂直平分线的性质和椭圆定义易求;(2)设出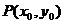 ,由中点坐标公式可得以PB为直径的圆的圆心
,由中点坐标公式可得以PB为直径的圆的圆心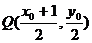 ,进而求出半径
,进而求出半径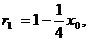 又圆
又圆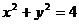 的圆心为
的圆心为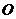 (0,0),半径
(0,0),半径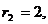 比较圆心距
比较圆心距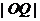 与
与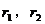 的大小关系即可.
的大小关系即可.
[答案](1)由点M是BN中点,又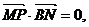
可知PM垂直平分BN,所以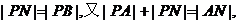
所以|PA|+|PB|=4
由椭圆定义知,点P的轨迹是以A,B为焦点的椭圆.
设椭圆方程为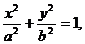
由
可知动点P的轨迹方程为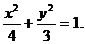
(2)解:设点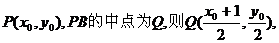

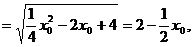
即以PB为直径的圆的圆心为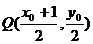 ,
,
半径为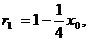
又圆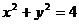 的圆心为
的圆心为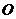 (0,0),半径
(0,0),半径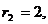
又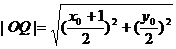
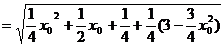
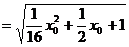

故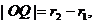 即两圆相切.
即两圆相切.
1.(山东省潍坊市2008届高三5月教学质量检测,理科,21)
已知实数m>1,定点A(-m,0),B(m,0),S为一动点,点S与A,B两点连线斜率之积
为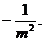
(1)求动点S的轨迹C的方程,并指出它是哪一种曲线;
(2)当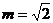 时,问t取何值时,直线
时,问t取何值时,直线 与曲线C有且只有一个交
与曲线C有且只有一个交
点?
(3)在(2)的条件下,证明:直线l上横坐标小于2的点P到点(1,0)的距离与到直线x=2的距离之比的最小值等于曲线C的离心率.
[解析](1)由题易得动点S的轨迹C为椭圆,注意要除去x轴上的两项点;(2)联立直线与椭圆方程,由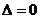 即可求得
即可求得 值,注意
值,注意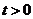 ;(3)由两点间的距离公式和点到直线的距离公式表示出两距离之比,转化成求关于
;(3)由两点间的距离公式和点到直线的距离公式表示出两距离之比,转化成求关于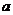 的函数
的函数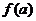 的最小值问题,利用导函数即可解之.
的最小值问题,利用导函数即可解之.
[答案](1)设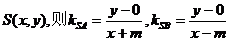 .
.
由题意得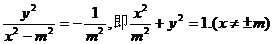
∵m>1,∴轨迹C是中心在坐标原点,焦点在x轴上的椭圆(除去x轴上的两项点),其中长轴长为2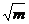 ,短轴长为2.
,短轴长为2.
(2)当m=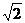 时,曲线C的方程为
时,曲线C的方程为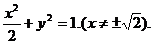
由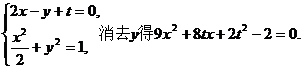
令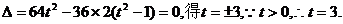
此时直线l与曲线C有且只有一个公共点.
(3)直线l方程为2x-y+3=0.
设点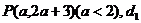 表示P到点(1,0)的距离,d2表示P到直线x=2的距离,
表示P到点(1,0)的距离,d2表示P到直线x=2的距离,
则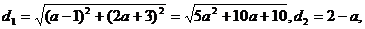
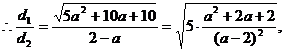
令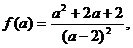
则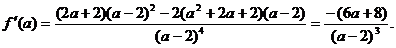
令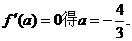
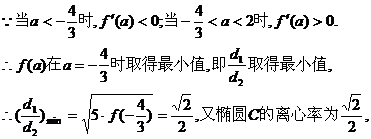
∴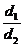 的最小值等于椭圆的离心率.
的最小值等于椭圆的离心率.
7.(2008年广东卷,文科,20)
设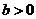 ,椭圆方程为
,椭圆方程为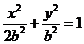 ,抛物线方程为
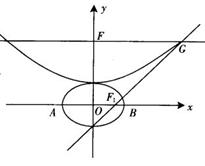
,抛物线方程为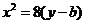 .如图所示,过点
.如图所示,过点 作
作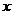 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为 ,已知抛物线在点
,已知抛物线在点 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点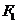 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设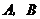 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点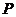 ,使得
,使得 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
[解析](1)由已知可求出G点的坐标,从而求出抛物线在点 的切线方程,进而求出
的切线方程,进而求出 点的坐标,由椭圆方程也可以求出
点的坐标,由椭圆方程也可以求出 点的坐标,从而求出
点的坐标,从而求出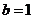 ,得出椭圆方程和抛物线方程;(2)以
,得出椭圆方程和抛物线方程;(2)以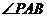 为直角和以
为直角和以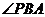 为直角的直角三角形显然各一个,以
为直角的直角三角形显然各一个,以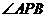 为直角的直角三角形是否存在可以转化成
为直角的直角三角形是否存在可以转化成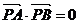 对应的方程是否有解的问题,从而可以求出满足条件的P点的个数.
对应的方程是否有解的问题,从而可以求出满足条件的P点的个数.
[答案](1)由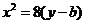 得
得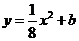 ,
,
当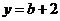 得
得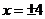 ,
,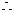 G点的坐标为
G点的坐标为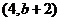 ,
,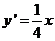 ,
,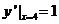 ,
,
过点G的切线方程为 即
即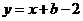 ,
,
令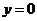 得
得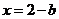 ,
,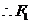 点的坐标为
点的坐标为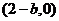 ,由椭圆方程得
,由椭圆方程得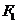 点的坐标为
点的坐标为 ,
,
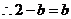 即
即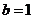 ,即椭圆和抛物线的方程分别为
,即椭圆和抛物线的方程分别为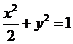 和
和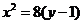 ;
;
(2)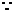 过
过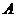 作
作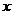 轴的垂线与抛物线只有一个交点
轴的垂线与抛物线只有一个交点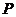 ,
,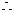 以
以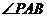 为直角的
为直角的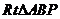 只有一个,
只有一个,
同理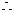 以
以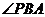 为直角的
为直角的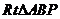 只有一个。
只有一个。
若以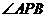 为直角,设
为直角,设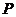 点坐标为
点坐标为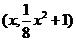 ,
,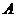 、
、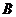 两点的坐标分别为
两点的坐标分别为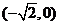 和
和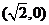 ,
,
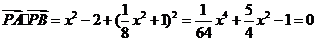 。
。
关于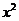 的二次方程有一大于零的解,
的二次方程有一大于零的解,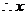 有两解,即以
有两解,即以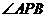 为直角的
为直角的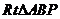 有两个,因此抛物线上存在四个点使得
有两个,因此抛物线上存在四个点使得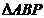 为直角三角形。
为直角三角形。
6.(2008年山东卷,文科,22)
已知曲线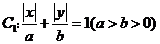 所围成的封闭图形的面积为
所围成的封闭图形的面积为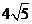 ,
,
曲线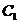 的内切圆半径为
的内切圆半径为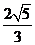 .记
.记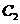 为以曲线
为以曲线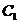 与坐标轴的交点为顶点的椭圆.
与坐标轴的交点为顶点的椭圆.
(Ⅰ)求椭圆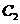 的标准方程;
的标准方程;
(Ⅱ)设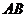 是过椭圆
是过椭圆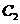 中心的任意弦,
中心的任意弦, 是线段
是线段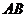 的垂直平分线.
的垂直平分线.
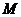 是
是 上异于椭圆中心的点.
上异于椭圆中心的点.
(1)若 (
(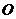 为坐标原点),当点
为坐标原点),当点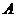 在椭圆
在椭圆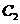 上运动时,
上运动时,
求点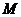 的轨迹方程;
的轨迹方程;
(2)若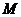 是
是 与椭圆
与椭圆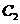 的交点,求
的交点,求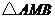 的面积的最小值.
的面积的最小值.
[解析](Ⅰ)由三角形面积公式和点到直线的距离公式可得关于a,b的方程组,
曲线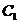 与坐标轴的交点为椭圆的顶点,显然
与坐标轴的交点为椭圆的顶点,显然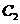 为焦点在x轴的椭圆;
为焦点在x轴的椭圆;
(Ⅱ)(1)设出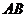 的方程
的方程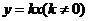 ,
,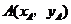 ,
,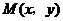 ,联立直线与椭圆得到方程组后,由
,联立直线与椭圆得到方程组后,由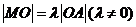 可得
可得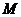 的轨迹方程,注意
的轨迹方程,注意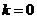 或不存在时所得方程仍然成立;(2)由直线
或不存在时所得方程仍然成立;(2)由直线 的方程:
的方程: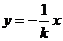 和椭圆方程联立后表示出
和椭圆方程联立后表示出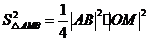 由不等式放缩即可求出最小值.
由不等式放缩即可求出最小值.
[答案](Ⅰ)由题意得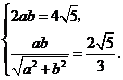 又
又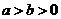 ,解得
,解得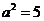 ,
,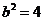 .
.
因此所求椭圆的标准方程为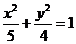 .
.
(Ⅱ)(1)假设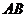 所在的直线斜率存在且不为零,设
所在的直线斜率存在且不为零,设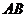 所在直线方程为
所在直线方程为
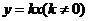 ,
,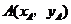 .
.
解方程组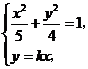 得
得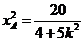 ,
,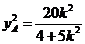 ,
,
所以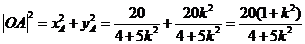 .
.
设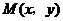 ,由题意知
,由题意知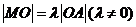 ,
,
所以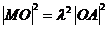 ,即
,即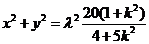 ,
,
因为 是
是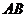 的垂直平分线,所以直线
的垂直平分线,所以直线 的方程为
的方程为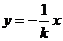 ,即
,即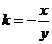 ,
,
因此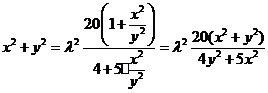 ,
,
又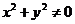 ,所以
,所以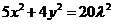 ,故
,故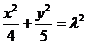 .
.
又当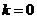 或不存在时,上式仍然成立.
或不存在时,上式仍然成立.
综上所述,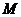 的轨迹方程为
的轨迹方程为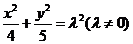 .
.
(2)当 存在且
存在且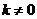 时,由(1)得
时,由(1)得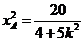 ,
,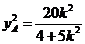 ,
,
由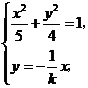 解得
解得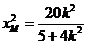 ,
,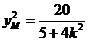 ,
,
所以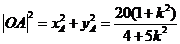 ,
,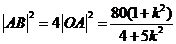 ,
,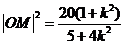 .
.
解法一:由于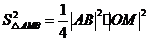
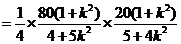


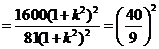 ,
,
当且仅当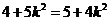 时等号成立,即
时等号成立,即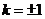 时等号成立,
时等号成立,
此时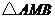 面积的最小值是
面积的最小值是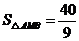 .
.
当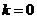 ,
,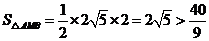 .
.
当 不存在时,
不存在时, .
.
综上所述, 的面积的最小值为
的面积的最小值为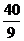 .
.
解法二:因为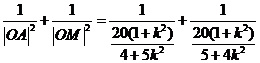
 ,
,
又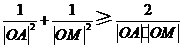 ,
,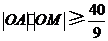 ,
,
当且仅当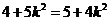 时等号成立,即
时等号成立,即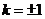 时等号成立,
时等号成立,
此时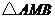 面积的最小值是
面积的最小值是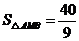 .
.
当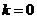 ,
,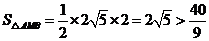 .
.
当 不存在时,
不存在时, .
.
综上所述,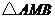 的面积的最小值为
的面积的最小值为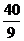 .
.
5. (2008年辽宁卷,文科,21)
在平面直角坐标系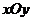 中,点P到两点
中,点P到两点 ,
,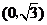 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 .
.
(Ⅰ)写出C的方程;
(Ⅱ)设直线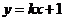 与C交于A,B两点.k为何值时
与C交于A,B两点.k为何值时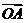
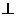
 ?此时
?此时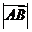 的值是多少?
的值是多少?
[解析](Ⅰ)由椭圆的定义易得,(Ⅱ)设出A,B两点的坐标后由一元二次方程根与系数关系求出 ,再由向量的坐标运算求出k值,最后由弦长公式可以求出
,再由向量的坐标运算求出k值,最后由弦长公式可以求出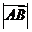 的值.
的值.
[答案](Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以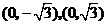 为焦点,
为焦点,
长半轴为2的椭圆.它的短半轴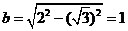 ,
,
故曲线C的方程为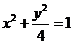 . 4分
. 4分
(Ⅱ)设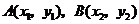 ,其坐标满足
,其坐标满足
 消去y并整理得
消去y并整理得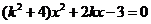 ,
,
故 . 6分
. 6分
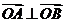 ,即
,即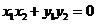 .而
.而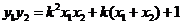 ,
,
于是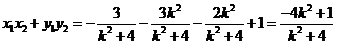 .
.
所以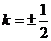 时,
时,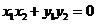 ,故
,故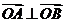 . 8分
. 8分
当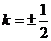 时,
时, ,
, .
.
 ,
,
而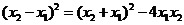
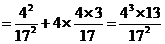 ,
,
所以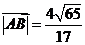 .
.
4.(2008年湖南卷,文科,19)
已知椭圆的中心在原点,一个焦点是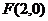 ,且两条准线间的距离为
,且两条准线间的距离为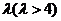 .
.
(I)求椭圆的方程;
(II)若存在过点A(1,0)的直线 ,使点F关于直线
,使点F关于直线 的对称点在椭圆上,
的对称点在椭圆上,
求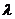 的取值范围.
的取值范围.
[解析](I)椭圆方程由a,b,c的关系易得,(II)设出直线 的方程,求出点F关于直线
的方程,求出点F关于直线 的对称点,代入椭圆方程解关于
的对称点,代入椭圆方程解关于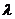 的不等式组即得
的不等式组即得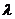 的取值范围.
的取值范围.
[答案](I)设椭圆的方程为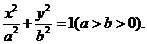
由条件知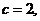 且
且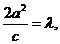 所以
所以
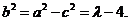
故椭圆的方程是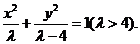
(II)依题意, 直线 的斜率存在且不为0,记为
的斜率存在且不为0,记为 ,则直线
,则直线 的方程是
的方程是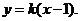
设点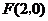 关于直线
关于直线 的对称点为
的对称点为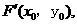 则
则
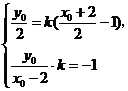 解得
解得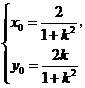
因为点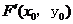 在椭圆上,所以
在椭圆上,所以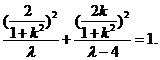 即
即
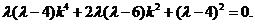
设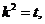 则
则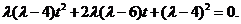
因为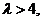 所以
所以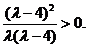 于是,
于是,
当且仅当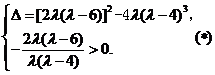
上述方程存在正实根,即直线 存在.
存在.
解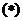 得
得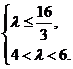 所以
所以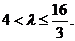
即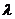 的取值范围是
的取值范围是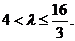
3.(2007年山东卷,理科,21)
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在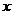 轴上,椭圆
轴上,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为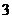 ,最小值为
,最小值为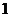 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若直线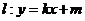 与椭圆
与椭圆 相交于
相交于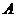 ,
,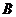 两点(
两点(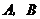 不是左右顶点),且以
不是左右顶点),且以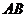 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
[解析](Ⅰ)由已知易求出a,c的值,即得椭圆方程,(Ⅱ)由待定系数法设出直线方程,联立椭圆方程后由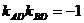 可以得到关于k和m的方程,求出满足
可以得到关于k和m的方程,求出满足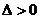 的k和m的关系式后即可得到过定点的直线方程.
的k和m的关系式后即可得到过定点的直线方程.
[答案](I)由题意设椭圆的标准方程为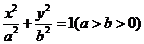
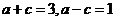 ,
,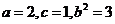
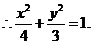
(II)设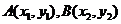 ,由
,由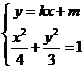 得
得
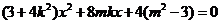 ,
,
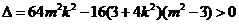 ,
, .
.
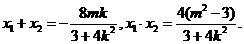
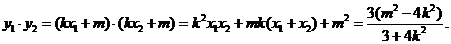
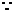 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点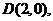
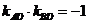 ,
,
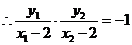 ,
,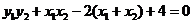 ,
,
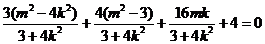 ,
,
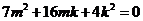 ,解得
,解得
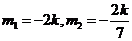 ,且满足
,且满足 .
.
当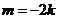 时,
时,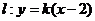 ,直线过定点
,直线过定点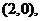 与已知矛盾;
与已知矛盾;
当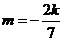 时,
时,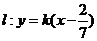 ,直线过定点
,直线过定点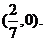
综上可知,直线 过定点,定点坐标为
过定点,定点坐标为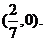
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com