
2.(2008全国二21).(本小题满分12分)
设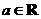 ,函数
,函数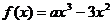 .
.
(Ⅰ)若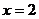 是函数
是函数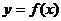 的极值点,求
的极值点,求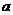 的值;
的值;
(Ⅱ)若函数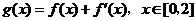 ,在
,在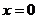 处取得最大值,求
处取得最大值,求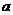 的取值范围.
的取值范围.
解:(Ⅰ)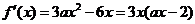 .
.
因为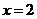 是函数
是函数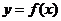 的极值点,所以
的极值点,所以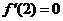 ,即
,即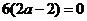 ,因此
,因此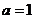 .
.
经验证,当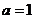 时,
时,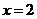 是函数
是函数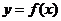 的极值点.············· 4分
的极值点.············· 4分
(Ⅱ)由题设,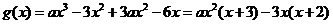 .
.
当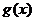 在区间
在区间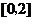 上的最大值为
上的最大值为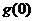 时,
时,
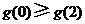 , 即
, 即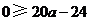 .故得
.故得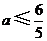 .··············· 9分
.··············· 9分
反之,当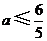 时,对任意
时,对任意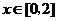 ,
,
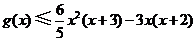
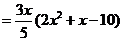
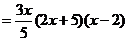
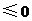 ,
,
而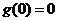 ,故
,故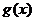 在区间
在区间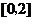 上的最大值为
上的最大值为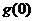 .
.
综上,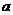 的取值范围为
的取值范围为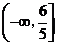 .······················ 12分
.······················ 12分
1.(2008全国一21).(本小题满分12分)(注意:在试题卷上作答无效)
已知函数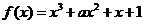 ,
,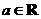 .
.
(Ⅰ)讨论函数 的单调区间;
的单调区间;
(Ⅱ)设函数 在区间
在区间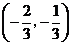 内是减函数,求
内是减函数,求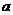 的取值范围.
的取值范围.
解:(1)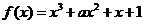
求导: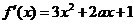
当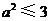 时,
时, ,
,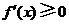
 在
在 上递增
上递增
当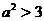 ,
,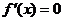 求得两根为
求得两根为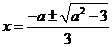
即 在
在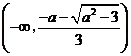 递增,
递增,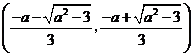 递减,
递减,
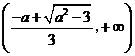 递增
递增
(2)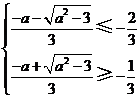 ,且
,且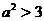 解得:
解得: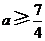
3.理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值.
2.熟记基本导数公式;掌握两个函数和、差、积、商的求导法则.了解复合函数的求导法则,会求某些简单函数的导数.
导数属于新增内容,是高中数学知识的一个重要的交汇点,命题范围非常广泛,为高考考查函数提供了广阔天地,处于一种特殊的地位,不但一定出大题而相应有小题出现。主要考查导数有关的概念、计算和应用。利用导数工具研究函数的有关性质,把导数应用于单调性、极值等传统、常规问题的同时,进一步升华到处理与自然数有关的不等式的证明,是函数知识和不等式知识的一个结合体,它的解题又融合了转化、分类讨论、函数与方程、数形结合等数学思想与方法,不但突出了能力的考查,同时也注意了高考重点与热点,这一切对考查考生的应用能力和创新意识都大有益处。
1.了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念.
(二)考点预测题
1. (2007年山东高考真题模拟试卷八,理科,22)
椭圆G: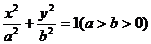 的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的
的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的
一点,且满足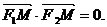
(Ⅰ)求离心率e的取值范围;
(Ⅱ)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为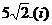 求此时
求此时
椭圆G的方程;(ⅱ)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q
为AB的中点,问A、B两点能否关于过点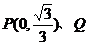 的直线对称?若能,求出k的取值
的直线对称?若能,求出k的取值
范围;若不能,请说明理由.
[答案](I)设M(x0,y0)
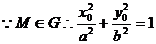 ①
①
又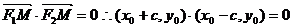 ②
②
由②得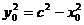 代入①式整理得
代入①式整理得 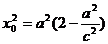
又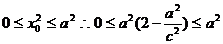
解得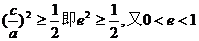
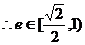
(Ⅱ)(i)当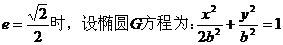
设H(x,y)为椭圆上一点,则
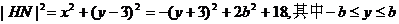
若0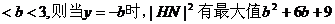
由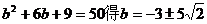 (舍去)
(舍去)
若b≥3,当y=-3时,|HN|2有最大值2b2+18
由2b2+18=50得b2=16
∴所求椭圆方程为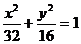
(ii)设A(x1,y1),B(x2,y2),Q(x0,y0),则由
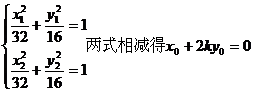 ③
③
又直线PQ⊥直线l ∴直线PQ方程为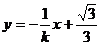
将点Q(x0,y0)代入上式得,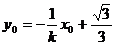 ④
④
由③④得Q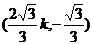
(解1)而Q点必在椭圆内部 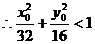
由此得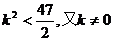

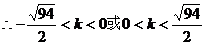
故当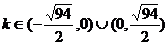 时A、B两点关于点P、Q的直线对称.
时A、B两点关于点P、Q的直线对称.
(解2)∴AB所在直线方程为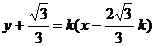
由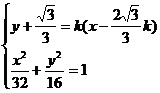 得
得
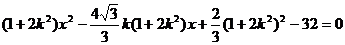
显然1+2k2≠0
而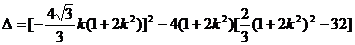
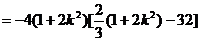
直线l与椭圆有两不同的交点A、B ∴△>0
解得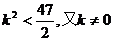
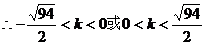
故当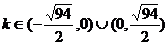 时,A、B两点关于点P、Q的直线对称。
时,A、B两点关于点P、Q的直线对称。
(ii)另解;设直线l的方程为y=kx+b
 由
由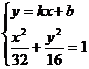 得
得
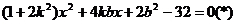
设A(x1,y1),B(x2,y2),Q(x0,y0),则
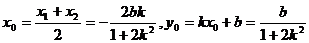 ③
③
又直线PQ⊥直线l ∴直线PQ方程为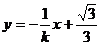
将点Q(x0,y0)代入上式得,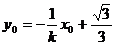 ④
④
将③代入④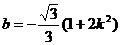 ⑤
⑤
∵x1,x2是(*)的两根
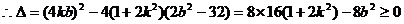 ⑥
⑥
⑤代入⑥得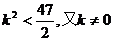
∴当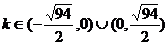 时,A、B两点关于点P、Q的直线对称
时,A、B两点关于点P、Q的直线对称
2.(2007年山东高考真题模拟试卷十一,理科,22)
双曲线M的中心在原点,并以椭圆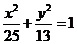 的焦点为焦点,以抛物线
的焦点为焦点,以抛物线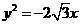 的
的
准线为右准线.
(Ⅰ)求双曲线M的方程;
(Ⅱ)设直线 :
: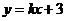 与双曲线M相交于A、B两点,O是原点.
与双曲线M相交于A、B两点,O是原点.
① 当 为何值时,使得
为何值时,使得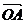
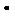
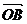
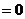 ?
?
② 是否存在这样的实数 ,使A、B两点关于直线
,使A、B两点关于直线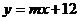 对称?若存在,求出
对称?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
[答案](Ⅰ)易知,椭圆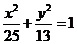 的半焦距为:
的半焦距为: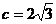 ,
,
又抛物线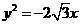 的准线为:
的准线为: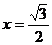 .
.
设双曲线M的方程为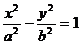 ,依题意有
,依题意有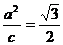 ,
,
故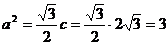 ,又
,又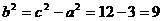 .
.
∴双曲线M的方程为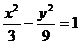 .
.
(Ⅱ)设直线 与双曲线M的交点为
与双曲线M的交点为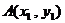 、
、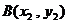 两点
两点
联立方程组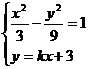 消去y得
消去y得 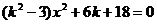 ,
,
 ∵
∵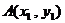 、
、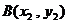 两点的横坐标是上述方程的两个不同实根, ∴
两点的横坐标是上述方程的两个不同实根, ∴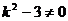
∴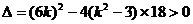
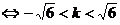 ,从而有
,从而有
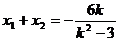 ,
,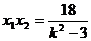 .
.
又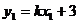 ,
,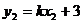
∴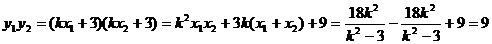 .
.
① 若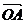
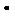
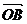
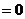 ,则有
,则有 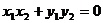 ,即
,即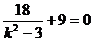
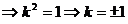 .
.
∴当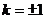 时,使得
时,使得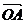
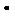
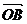
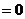 .
.
② 若存在实数 ,使A、B两点关于直线
,使A、B两点关于直线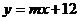 对称,则必有
对称,则必有 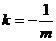 ,
,
因此,当m=0时,不存在满足条件的k;
当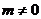 时,由
时,由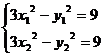 得
得 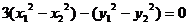
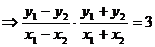
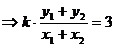
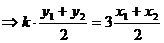
∵A、B中点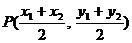 在直线
在直线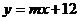 上,
上,
∴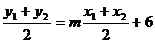 代入上式得
代入上式得
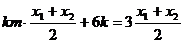
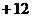 ;又
;又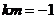 , ∴
, ∴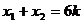
将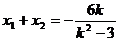 代入并注意到
代入并注意到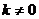 ,得
,得 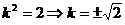 .
.
∴当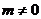 时,存在实数
时,存在实数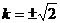 ,使A、B两点关于直线
,使A、B两点关于直线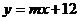 对称.
对称.
3.(2008年山东卷,理科,22)
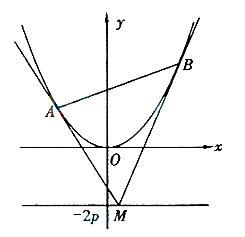 如图,设抛物线方程为
如图,设抛物线方程为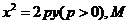 为直线
为直线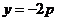 上任意一点,过
上任意一点,过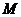 引抛物线的切线,切点分别为
引抛物线的切线,切点分别为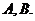
(I)求证: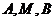 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(II)已知当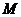 点的坐标为
点的坐标为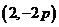 时,
时,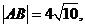 求此时抛物线的方程;
求此时抛物线的方程;
(III)是否存在点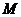 ,使得点
,使得点 关于直线
关于直线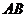 的对称点
的对称点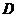 在抛物线
在抛物线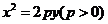 上,其中点
上,其中点 满足
满足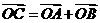 (
(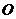 为坐标原点)。若存在,求出所有适合题意的点的坐标;若不存在,请说明理由。
为坐标原点)。若存在,求出所有适合题意的点的坐标;若不存在,请说明理由。
[答案](I)证明:由题意设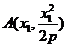 ,
,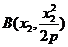 ,
,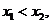
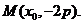
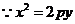 ,
,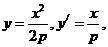
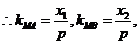
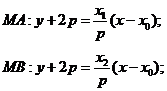

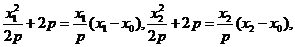
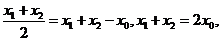
所以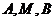 三点的横坐标成等差数列。
三点的横坐标成等差数列。
(II)解:由(I)知,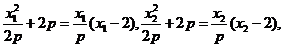
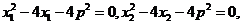
所以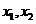 是方程
是方程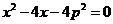 的两根,
的两根,
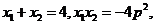
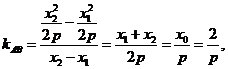
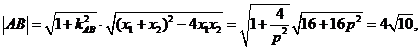
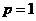 或
或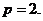
因此所求抛物线方程为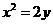 或
或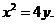
(III)解:设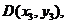 由题意得
由题意得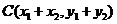 ,则
,则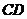 中点坐标为
中点坐标为
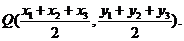
设直线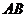 的方程为
的方程为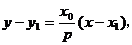
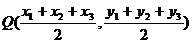 与
与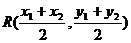 都在
都在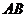 上,代入得
上,代入得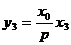 .
.
若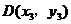 在抛物线上,则
在抛物线上,则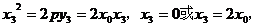 即
即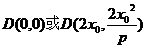 .
.
1)当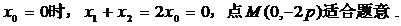
2)当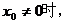
(1)对于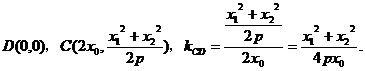
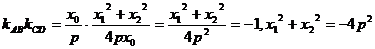 矛盾.
矛盾.
(2)对于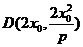 ,
,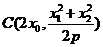 ,则
,则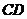 与
与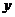 轴平行,而
轴平行,而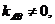 直线
直线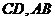 不垂直矛盾。
不垂直矛盾。
综上可知,仅存在一点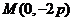 适合题意.
适合题意.
(一)文字介绍
圆锥曲线是解析几何的核心内容,也是高考命题的热点之一.高考对圆锥曲线的考查,总体上是以知识应用和问题探究为主,一般是给出曲线方程,讨论曲线的基本元素和简单的几何性质;或给出曲线满足的条件,判断(求)其轨迹;或给出直线与曲线、曲线与曲线的位置关系,讨论与其有关的其他问题(如直线的方程、直线的条数、弦长、曲线中参变量的取值范围等);或考查圆锥曲线与其他知识综合(如不等式、函数、向量、导数等)的问题等.
8. (辽宁省抚顺一中2009届高三第一次模拟考试,理科,21)
椭圆ax2+by2 =1与直线x+y-1=0相交于A、B两点,若|AB|=2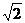 ,线段AB的中点为C,且OC的斜率为
,线段AB的中点为C,且OC的斜率为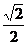 ,求椭圆方程.
,求椭圆方程.
[解析]联立直线与椭圆方程,根据一元二次方程根与系数关系、中点坐标公式、斜率公式求出a,b的关系,再由弦长公式求出a,b的值,即得所求椭圆的方程.
[答案]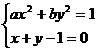 ∴(a+b)x2 -2bx+b-1=0
∴(a+b)x2 -2bx+b-1=0
∴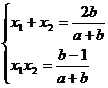
C(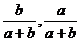 )
)
KOC =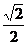 ∴b=
∴b=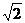 a,
a,
代入|AB|=2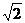 ,即:(1+k2)[(x1+x2)2-4 x1x2]=8
,即:(1+k2)[(x1+x2)2-4 x1x2]=8
a=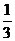 ,b=
,b=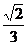
∴椭圆方程为: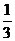 x2+
x2+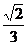 y2 =1
y2 =1
7. (江苏省盐城一中、大丰中学、建湖中学2009届高三第二次调研考试, 21)
抛物线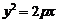 的准线的方程为
的准线的方程为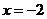 ,该抛物线上的每个点到准线
,该抛物线上的每个点到准线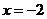 的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线
的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线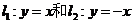 相切的圆,
相切的圆,
(Ⅰ)求定点N的坐标;
(Ⅱ)是否存在一条直线 同时满足下列条件:
同时满足下列条件:
①  分别与直线
分别与直线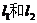 交于A、B两点,且AB中点为
交于A、B两点,且AB中点为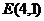 ;
;
②  被圆N截得的弦长为
被圆N截得的弦长为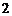 .
.
[解析](1)由抛物线的定义易得;
(2)假设存在直线 ,设出直线
,设出直线 的方程为
的方程为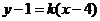 ,
,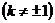 .
.
方法1:由弦心距的长为1求出 的值,然后检验是否符合AB中点为
的值,然后检验是否符合AB中点为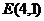 这个条件;
这个条件;
方法2:将直线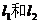 的方程分别与直线
的方程分别与直线 的方程联立,求出A、B两点的坐标,再由中点坐标公式求出
的方程联立,求出A、B两点的坐标,再由中点坐标公式求出 的值,最后检验弦心距的长是否为1;
的值,最后检验弦心距的长是否为1;
方法3:设出A点的坐标为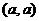 ,由中点坐标公式和B点在
,由中点坐标公式和B点在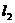 上,求出
上,求出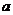 的值,进而求出直线
的值,进而求出直线 的斜率,最后检验弦心距的长是否为1.
的斜率,最后检验弦心距的长是否为1.
[答案](1)因为抛物线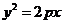 的准线的方程为
的准线的方程为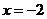
所以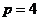 ,根据抛物线的定义可知点N是抛物线的焦点,
,根据抛物线的定义可知点N是抛物线的焦点,
所以定点N的坐标为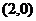
(2)假设存在直线 满足两个条件,显然
满足两个条件,显然 斜率存在,
斜率存在,
设 的方程为
的方程为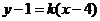 ,
,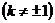
以N为圆心,同时与直线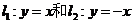 相切的圆N的半径为
相切的圆N的半径为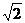 ,
,
方法1:因为 被圆N截得的弦长为2,所以圆心到直线的距离等于1,
被圆N截得的弦长为2,所以圆心到直线的距离等于1,
即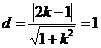 ,解得
,解得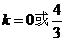 ,
,
当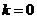 时,显然不合AB中点为
时,显然不合AB中点为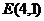 的条件,矛盾!
的条件,矛盾!
当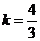 时,
时, 的方程为
的方程为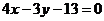
由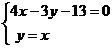 ,解得点A坐标为
,解得点A坐标为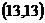 ,
,
由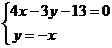 ,解得点B坐标为
,解得点B坐标为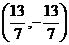 ,
,
显然AB中点不是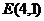 ,矛盾!
,矛盾!
所以不存在满足条件的直线 .
.
方法2:由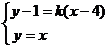 ,解得点A坐标为
,解得点A坐标为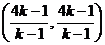 ,
,
由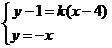 ,解得点B坐标为
,解得点B坐标为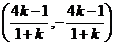 ,
,
因为AB中点为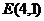 ,所以
,所以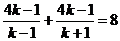 ,解得
,解得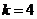 ,
,
所以 的方程为
的方程为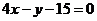 ,
,
圆心N到直线 的距离
的距离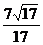 ,
,
因为 被圆N截得的弦长为2,所以圆心到直线的距离等于1,矛盾!
被圆N截得的弦长为2,所以圆心到直线的距离等于1,矛盾!
所以不存在满足条件的直线 .
.
方法3:假设A点的坐标为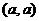 ,
,
因为AB中点为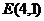 ,所以B点的坐标为
,所以B点的坐标为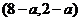 ,
,
又点B 在直线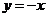 上,所以
上,所以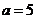 ,
,
所以A点的坐标为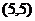 ,直线
,直线 的斜率为4,
的斜率为4,
所以 的方程为
的方程为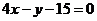 ,
,
圆心N到直线 的距离
的距离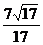 ,
,
因为 被圆N截得的弦长为2,所以圆心到直线的距离等于1,矛盾!
被圆N截得的弦长为2,所以圆心到直线的距离等于1,矛盾!
所以不存在满足条件的直线 .
.
6. (山东省文登市2009届高三第三次月考试题,理科,21)
过点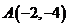 作倾斜角为
作倾斜角为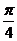 的直线,交抛物线
的直线,交抛物线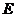 :
: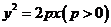 于
于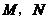 两点,且
两点,且
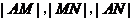 成等比数列。⑴求
成等比数列。⑴求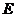 的方程;⑵过点
的方程;⑵过点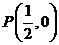 的直线
的直线 与曲线
与曲线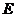 交于
交于

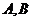 两点。设
两点。设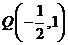 ,
,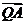 与
与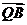 的夹角为
的夹角为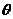 ,
,
求证: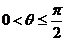 。
。
[解析]⑴设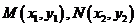 ,联立直线与抛物线的方程
,联立直线与抛物线的方程
后根据一元二次方程根与系数关系可得到关于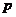 的方程,解之即得
的方程,解之即得
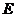 的方程;⑵法一:要证
的方程;⑵法一:要证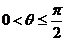 ,只需证明
,只需证明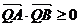 即可.
即可.
法二:根据“以抛物线焦点弦为直径的圆与准线相切”这一性质分两种情况讨论即可得证.
[答案]⑴设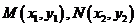 ,则由题
,则由题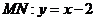 ,由
,由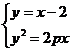 得
得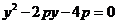 ,故
,故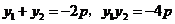 。
。
又根据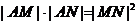 可得
可得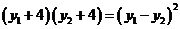 ,即
,即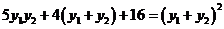 ,代入可得
,代入可得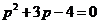 ,解得
,解得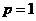 (舍负)。故
(舍负)。故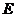 的方程为
的方程为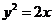 ;
;
⑵法一:设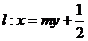 ,代入
,代入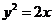 得
得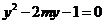 ,故
,故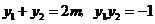 ,
,
从而
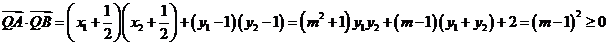 ,因此
,因此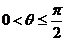
法二:显然点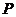 是抛物线
是抛物线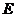 的焦点,点
的焦点,点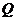 是其准线
是其准线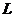 上一点。设
上一点。设 为
为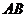 的中点,过
的中点,过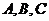 分别作
分别作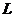 的垂线,垂足分别为
的垂线,垂足分别为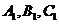 ,则
,则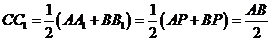 。因此以
。因此以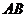 为直径的圆与准线
为直径的圆与准线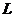 相切(于点
相切(于点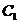 )。若
)。若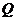 与
与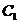 重合,则
重合,则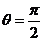 。否则点
。否则点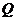 在
在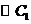 外,因此
外,因此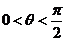 。综上知
。综上知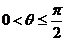 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com