
9、如图,ABCD为矩形,PA 平面ABCD ,M、N分别为AB、PC的中点,
平面ABCD ,M、N分别为AB、PC的中点,
(1)
证明:AB MN; (2)若平面PDC与平面ABCD成
MN; (2)若平面PDC与平面ABCD成 角,证明:平面MND
角,证明:平面MND 平面PDC。
平面PDC。

8、是 所在平面外一点,
所在平面外一点, 分别是
分别是 的重心,
的重心,
(1)求证:平面 ; (2)求
; (2)求
7、正四棱柱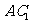 的底面边长为3,侧棱长为4,则两平行平面
的底面边长为3,侧棱长为4,则两平行平面 与平面
与平面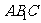 的距离是
的距离是
6、直线AB与直二面角 的两个半平面分别相交于A、B两点,且A、B均不在棱上,如果直线AB与
的两个半平面分别相交于A、B两点,且A、B均不在棱上,如果直线AB与 所成的角分别为
所成的角分别为 ,那么
,那么 的取值范围是
的取值范围是
5、在斜三棱柱 的底面
的底面 中,
中, 且
且 ,过
,过 底面ABC,垂足为H,则点H在(
)
底面ABC,垂足为H,则点H在(
)
A、直线AC上 B、直线AB上 C、直线BC上 D、 的内部
的内部
4、如果 ||
|| ,AB和CD是夹在平面
,AB和CD是夹在平面 、
、 之间的两条线段,AB
之间的两条线段,AB CD,且AB=2,直线AB与平面
CD,且AB=2,直线AB与平面 成
成 角,那么线段CD的取值范围是( )
角,那么线段CD的取值范围是( )
A、 B、
B、 C、
C、 D、
D、
3、已知平面 ||平面
||平面 ,P是
,P是 、
、 外一点,过点P的直线
外一点,过点P的直线 与
与 、
、 分别交于A、C,过点P的直线
分别交于A、C,过点P的直线 与
与 、
、 分别交于B 、D,且PA=6,AC=9, PD=8;则BD的长为( )
分别交于B 、D,且PA=6,AC=9, PD=8;则BD的长为( )
A、16 B、24或 C、14
D、20
C、14
D、20
2、设 、
、 、
、 为平面,给出下列条件:(1)
为平面,给出下列条件:(1)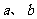 为异面直线,
为异面直线, ,(2)
,(2) 内距离为
内距离为 的平行直线在
的平行直线在 内射影仍为两条距离为
内射影仍为两条距离为 的平行线;(3)
的平行线;(3) 内不共线的三点到
内不共线的三点到 的距离相等;(4)
的距离相等;(4) ;其中能使
;其中能使 ||
|| 成立的条件的个数为( )
成立的条件的个数为( )
A、1 B、2 C、3 D、4
1、若有平面 则下列命题中的假命为( )
则下列命题中的假命为( )
A、过点P且垂直于 的直线平行于
的直线平行于 ; B、过点P且垂直于
; B、过点P且垂直于 的平面垂直于
的平面垂直于 ;
;
C、过点P且垂直于 的直线在
的直线在 内; D、过点P且垂直于
内; D、过点P且垂直于 的直线在
的直线在 内;
内;
例1.正方体ABCD-A1B1C1D1中.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E、F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
 证明:(1)由B1B∥DD1,得四边形BB1D1D是平行四边形,
证明:(1)由B1B∥DD1,得四边形BB1D1D是平行四边形,
∴B1D1∥BD,
又BD Ë平面B1D1C,B1D1 平面B1D1C,
平面B1D1C,
∴BD∥平面B1D1C.
同理A1D∥平面B1D1C.
而A1D∩BD=D,
∴平面A1BD∥平面B1CD.
(2)由BD∥B1D1,得BD∥平面EB1D1.
取BB1中点G,∴AE∥B1G.
从而得B1E∥AG,同理GF∥AD.
∴AG∥DF.
∴B1E∥DF.
∴DF∥平面EB1D1.
∴平面EB1D1∥平面FBD.
说明 要证“面面平面”只要证“线面平面”,要证“线面平行”,只要证“线线平面”,故问题最终转化为证线与线的平行.
 例2.在四面体
例2.在四面体 中,
中, ,且
,且 ,
,
求证:平面 ⊥平面
⊥平面
例3.如图, 为正三角形,
为正三角形, 平面
平面 ,
, ,且
,且 ,
, 是
是 的中点,
的中点,
 求证:(1)
求证:(1) ;(2)平面
;(2)平面 平面
平面 ;(3)平面
;(3)平面 平面
平面 。
。
例4三棱锥 中,
中, ,点
,点 为
为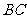 中点,
中点, 于
于 点,连
点,连 ,求证:平面
,求证:平面 平面
平面
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com