2、基本概念

(1)　　　 (2)　 (3)

(4)

1、直线运动的条件：①F_合=0或②F_合≠0且F_合与v共线，a与v共线。(回忆曲线运动的条件)

13、

解析：设卡车的质量为M，车所受阻力与车重之比为；刹车前卡车牵引力的大小为，

卡车刹车前后加速度的大小分别为和。重力加速度大小为g。由牛顿第二定律有

设车厢脱落后，内卡车行驶的路程为，末速度为，根据运动学公式有

　　　 ⑤

　　　　　 ⑥

　　　　　 ⑦

式中，是卡车在刹车后减速行驶的路程。设车厢脱落后滑行的路程为，有

　　　　　 ⑧

卡车和车厢都停下来后相距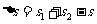　　　 ⑨

由①至⑨式得　 10

带入题给数据得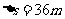　　　　　　　　 11

评分参考：本题9分。①至⑧式各1分，11式1分

12、

解析：

(1)第一次飞行中，设加速度为

匀加速运动

由牛顿第二定律

解得

(2)第二次飞行中，设失去升力时的速度为，上升的高度为

匀加速运动

设失去升力后的速度为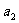，上升的高度为

由牛顿第二定律

解得

(3)设失去升力下降阶段加速度为；恢复升力后加速度为，恢复升力时速度为

由牛顿第二定律

F+f-mg=ma₄

且

V₃₌a₃t₃

解得t₃=(s)(或2.1s)

11、答案：440N，275N

解析：解法一:(1)设运动员受到绳向上的拉力为F，由于跨过定滑轮的两段绳子拉力相等，吊椅受到绳的拉力也是F。对运动员和吊椅整体进行受力分析如图所示，则有：

由牛顿第三定律，运动员竖直向下拉绳的力

(2)设吊椅对运动员的支持力为F_N，对运动员进行受力分析如图所示，则有：

由牛顿第三定律，运动员对吊椅的压力也为275N

解法二:设运动员和吊椅的质量分别为M和m；运动员竖直向下的拉力为F，对吊椅的压力大小为F_N。

根据牛顿第三定律，绳对运动员的拉力大小为F，吊椅对运动员的支持力为F_N。分别以运动员和吊椅为研究对象，根据牛顿第二定律

　　　　　　　　　　　　　　　　　　 ①

　　　　　　　　　　　　　　　　　　 ②

由①②得　　　

10、解析：(1)设货物滑到圆轨道末端是的速度为，对货物的下滑过程中根据机械能守恒定律得，①

设货物在轨道末端所受支持力的大小为,根据牛顿第二定律得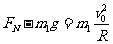，②

联立以上两式代入数据得③

根据牛顿第三定律，货物到达圆轨道末端时对轨道的压力大小为3000N，方向竖直向下。

(2)若滑上木板A时，木板不动，由受力分析得④

若滑上木板B时，木板B开始滑动，由受力分析得⑤

联立④⑤式代入数据得⑥。

(3)，由⑥式可知，货物在木板A上滑动时，木板不动。设货物在木板A上做减速运动时的加速度大小为，由牛顿第二定律得⑦

设货物滑到木板A末端是的速度为，由运动学公式得⑧

联立①⑦⑧式代入数据得⑨

设在木板A上运动的时间为t，由运动学公式得⑩

联立①⑦⑨⑩式代入数据得。

考点：机械能守恒定律、牛顿第二定律、运动学方程、受力分析

9、

答案：BC

解析：受力分析可知，下滑时加速度为，上滑时加速度为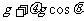，所以C正确。设下滑的距离为l，根据能量守恒有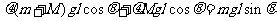，得m＝2M。也可以根据除了重力、弹性力做功以外，还有其他力(非重力、弹性力)做的功之和等于系统机械能的变化量，B正确。在木箱与货物从顶端滑到最低点的过程中，减少的重力势能转化为弹簧的弹性势能和内能，所以D不正确。

考点：能量守恒定律，机械能守恒定律，牛顿第二定律，受力分析

提示：能量守恒定律的理解及应用。

8、答案：BC

解析：飞船点火变轨，前后的机械能不守恒，所以A不正确。飞船在圆轨道上时万有引力来提供向心力，航天员出舱前后都处于失重状态，B正确。飞船在此圆轨道上运动的周期90分钟小于同步卫星运动的周期24小时，根据可知，飞船在此圆轨道上运动的角度速度大于同步卫星运动的角速度，C正确。飞船变轨前通过椭圆轨道远地点时只有万有引力来提供加速度，变轨后沿圆轨道运动也是只有万有引力来提供加速度，所以相等，D不正确。

考点：机械能守恒定律，完全失重，万有引力定律

提示：若物体除了重力、弹性力做功以外，还有其他力(非重力、弹性力)不做功，且其他力做功之和不为零，则机械能不守恒。

根据万有引力等于卫星做圆周运动的向心力可求卫星的速度、周期、动能、动量等状态量。由得，由得，由得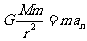，可求向心加速度。

7、答案：B

解析：由图甲可知前两秒物体做初速度为零的匀加速直线运动，所以前两秒受力恒定，2s-4s做正方向匀加速直线运动，所以受力为负，且恒定，4s-6s做负方向匀加速直线运动，所以受力为负，恒定，6s-8s做负方向匀减速直线运动，所以受力为正，恒定，综上分析B正确。

考点：v-t图象、牛顿第二定律

提示：在v-t图象中倾斜的直线表示物体做匀变速直线运动，加速度恒定，受力恒定。

6、答案：D

解析：当为F时有，当为2F时有，可知，D对。