
7.某人用20元购进1元一朵的康乃馨和2元一朵的玫瑰进行推销,康乃馨售价2元,玫瑰售价5元.假设他购入的花能全部售完,为使利润超过25元,有几种不同的进货方式?
解:设购入x朵康乃馨,调朵玫瑰,(x,y∈N),由已知得

由①②得y≥5;由①③得y≤10.
∴y=5,6,7,8,9,10.同理25-3y≤x≤20-2y.
当y=5时,x=10; 当y=6时,x=7,8. 当y=7时,x=4,5,6;
当y=8时,x=1,2,3,4; 当y=9时,x=0,1,2; 当y=10时,x=0.
综上知,共有1+2+3+4+3+1=14种.
6.组合问题,直接法:选派5名医生分为2男3女,3男2女,4男1女,5男这四类,故(2)正确;
间接法: 不考虑限制条件,选派方法有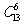 种,需剔除的有1男4女,5女两类,故(3)正确. 因此结论为: (2)(3)
种,需剔除的有1男4女,5女两类,故(3)正确. 因此结论为: (2)(3)
[解答题]
6.有13名医生,其中女医生6人 现从中抽调5名医生组成医疗小组前往灾区,若医疗小组至少有2名男医生,同时至多有3名女医生,设不同的选派方法种数为P,则下列等式
现从中抽调5名医生组成医疗小组前往灾区,若医疗小组至少有2名男医生,同时至多有3名女医生,设不同的选派方法种数为P,则下列等式
①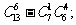 ②
②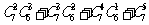 ;
;
③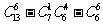 ; ④
; ④ ;
;
其中能成为P 的算式有_________种
◆练习简答:1.A; 2.B; 3.90种; 4.4576; 5. 48;
5.(2006辽宁)5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_____种.(以数作答)
4.(2005辽宁)用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1和2相邻,3与4相邻,5与6相邻,而7与8不相邻,这样的八位数共有 个.(用数字作答)
3.某年级有6个班,派3个数学老师任教,每位教师教两个班,不同的任课方法种数有_______种.
2.(2005湖南)4位同学参加某种形式的竞赛,竞赛规则规定:每位同学必须从甲.乙两道题中任选一题作答,选甲题答对得100分,答错得-100分;选乙题答对得90分,答错得-90分.若4位同学的总分为0,则这4位同学不同得分情况的种数是( )
A.48 B.36 C.24 D.18
[填空题]
1.(2006天津)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )
A.10种 B.20种 C.36种 D.52种
3. 记住一些常题型的特殊解法;如捆绑法,插空法, 排除法, 插板法,分组、分配等.
同步练习 10.3排列组全的综合应用
[选择题]
2.对于有附加条件的排列组合应用题,应掌握以下基本方法与技巧
(1)特殊元素优先安排;(2)合理分类与准确分步;(3)先选后排;(4)相邻问题捆绑处理;(5)不相邻问题插空处理;(6)定序问题排除法处理;(7)分排问题直排处理;(8)“小集团”排列问题先整体后局部;(9)构造模型;(10)正难则反,等价转化.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com