
1. 我国古代臣子写给君王的呈文有各种不同的名称, 战国时期称”书”, 到了汉代, 则分为:章,奏,表,议四类.刘勰《文心雕龙·章表篇》说“章以谢恩,奏以按劾,表以陈情,议以执异”,可见表虽是一种公文文体,但并不是表达对国家大事的意见主张,而只是古代臣子为了向皇帝陈述自己的请求而使用的文体,因此,奏议类的公文是以议论为主,而章表类的公文则是以抒情为主。中国文学史上有一些著名的以“表”这种文体写作的文章,历来收到人们的称道,如孔融的《荐祢衡表》、曹植的《求自试表》、诸葛亮的《出师表》、李密的《陈情表》。
12.(2010·南通模拟)已知函数f(x)=x3+ax2+bx+c在x=-与x=1时都取得极值,
(1)求a,b的值与函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
解:(1)f(x)=x3+ax2+bx+c,f′(x)=3x2+2ax+b,
由f′(-)=-a+b=0,f′(1)=3+2a+b=0得a=-,b=-2,
f′(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
|
x |
(-∞,-) |
- |
(-,1) |
1 |
(1,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
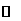 ? ? |
极大值 |
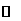 ? ? |
极小值 |
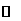 ? ? |
所以函数f(x)的递增区间是(-∞,-)与(1,+∞),递减区间(-,1);
(2)f(x)=x3-x2-2x+c,x∈[-1,2],当x=-时,f(-)=+c为极大值,而f(2)=2+c,则f(2)=2+c为最大值,要使f(x)<c2,x∈[-1,2]恒成立,则只需要c2>f(2)=2+c,得c<-1,或c>2.
11.设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,不可能正确的是 ( )

解析:对于图A来说,抛物线为函数f(x),直线为f′(x);对于图B来说,上凸的曲线为函数f(x),下凹的曲线为f′(x);对于图C来说,下面的曲线为函数f(x),上面的曲线f′(x).只有图D不符合题设条件.
答案:D
10.某公司生产某种产品,固定成本为20 000元,每生产一单位产品,成本增加100
元,已知总营业收入R与年产量x的关系是R=R(x)=
,则总利润最大时,每年生产的产品是 ( )
A.100 B.150 C.200 D.300
解析:由题意得,总成本函数为C=C(x)=20 000+100x,
所以总利润函数为
P=P(x)=R(x)-C(x)
=
而P′(x)=
令P′(x)=0,得x=300,易知x=300时,P最大.
答案:D
9.已知对任意实数x,都有f(-x)=-f(x),g(-x)=g(x),且x>0时, f′(x)>0,g′(x)>0,则x<0时 ( )
A.f′(x)>0,g′(x)>0 B.f′(x)>0,g′(x)<0
C.f′(x)<0,g′(x)>0 D.f′(x)<0,g′(x)<0
解析:由题意知f(x)是奇函数,g(x)是偶函数.当x>0时,f(x),g(x)都单调递增,则当x<0时,f(x)单调递增,g(x)单调递减,即f′(x)>0,g′(x)<0.
答案:B
8.(文)已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为,若x=时,y=f(x)有极值,
(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
解:(1)由f(x)=x3+ax2+bx+c,得
f′(x)=3x2+2ax+b.
当x=1时,切线l的斜率为3,可得2a+b=0. ①
当x=时,y=f(x)有极值,则f′()=0,可得
4a+3b+4=0. ②
由①②解得a=2,b=-4.
设切线l的方程为y=3x+m.
由原点到切线l的距离为,则=,
解得m=±1.
∵切线l不过第四象限,∴m=1.
由于切点的横坐标为x=1,∴f(1)=4.
∴1+a+b+c=4,∴c=5;
(2)由(1)可得f(x)=x3+2x2-4x+5,
∴f′(x)=3x2+4x-4.
令f′(x)=0,得x=-2,x=.
 f(x)和f′(x)的变化情况如下表:
f(x)和f′(x)的变化情况如下表:
|
x |
[-3,-2) |
-2 |
(-2,) |
|
(,1] |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
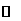 ? ? |
极大值 |
 ? ? |
极小值 |
 ? ? |
∴f(x)在x=-2处取得极大值f(-2)=13,
在x=处取得极小值f()=.
又f(-3)=8,f(1)=4,
∴f(x)在[-3,1]上的最大值为13,最小值为.
(理)已知函数f(x)=x3+2bx2+cx-2的图象在与x轴交点处的切线方程是y=5x-10.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+mx,若g(x)的极值存在,求实数m的取值范围以及函数g(x)取得极值时对应的自变量x的值.
解:(1)由已知,切点为(2,0),故有f(2)=0,
即4b+c+3=0. ①
f′(x)=3x2+4bx+c,由已知,f′(2)=12+8b+c=5.
得8b+c+7=0. ②
联立①、②,解得c=1,b=-1,
于是函数解析式为f(x)=x3-2x2+x-2.
(2)g(x)=x3-2x2+x-2+mx,
g′(x)=3x2-4x+1+,令g′(x)=0.
当函数有极值时,Δ≥0,方程3x2-4x+1+=0有实根,
由Δ=4(1-m)≥0,得m≤1.
①当m=1时,g′(x)=0有实根x=,在x=左右两侧均有g′(x)>0,故函数g(x)无极值.
②当m<1时,g′(x)=0有两个实根,
x1=(2-),x2=(2+),
当x变化时,g′(x)、g(x)的变化情况如下表:
|
x |
(-∞,x1) |
x1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
g′(x) |
+ |
0 |
- |
0 |
+ |
|
g(x) |
? |
极大值 |
? |
极小值 |
? |
故在m∈(-∞,1)时,函数g(x)有极值;
当x=(2-)时g(x)有极大值;
当x=(2+)时g(x)有极小值.
|
题组三 |
导数的综合应用 |
7.函数y=sin2x-x,x∈[-,]的最大值是________,最小值是________.
解析:∵y′=2cos2x-1=0,∴x=±.
而f(-)=-+,f()=-,
端点f(-)=,f()=-,
所以y的最大值是,最小值是-.
答案: -
6.若函数f(x)=x3-3x+a有3个不同的零点,则实数a的取值范围是 ( )
A.(-2,2) B.[-2,2] C.(-∞,-1) D.(1,+∞)
解析:由f′(x)=3x2-3=3(x-1)(x+1),
且当x<-1时,f′(x)>0;
当-1<x<1时,f′(x)<0;当x>1时,f′(x)>0.
所以当x=-1时函数f(x)有极大值,当x=1时函数f(x)有极小值.
要使函数f(x)有3个不同的零点,只需满足
解之得-2<a<2.
答案:A
5.(文)函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a= ( )
A.2 B.3 C.4 D.5
解析:因为f(x)=x3+ax2+3x-9,所以f′(x)=3x2+2ax+3,由题意有f′(-3)=0,所以3×(-3)2+2a×(-3)+3=0,由此解得a=5.
答案:D
(理)设a∈R,若函数y=ex+ax,x∈R有大于零的极值点,则 ( )
A.a<-1 B.a>-1 C.a>- D.a<-
解析:由y′=(ex+ax)′=ex+a=0得ex=-a,
即x=ln(-a)>0⇒-a>1⇒a<-1.
答案:A
4.设函数f(x)=x3+ax2-9x-1(a<0).若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行,求:
(1)a的值;
(2)函数f(x)的单调区间.
解:(1)因f(x)=x3+ax2-9x-1,
所以f′(x)=3x2+2ax-9
=32-9-.
即当x=-时,f′(x)取得最小值-9-.
因斜率最小的切线与12x+y=6平行,即该切线的斜率为-12,所以-9-=-12,即a2=9.
解得a=±3,由题设a<0,所以a=-3.
(2)由(1)知a=-3,因此f(x)=x3-3x2-9x-1,
f′(x)=3x2-6x-9=3(x-3)(x+1),
令f′(x)=0,解得x1=-1,x2=3.
当x∈(-∞,-1)时,f′(x)>0,
故f(x)在(-∞,-1)上为增函数;
当x∈(-1,3)时,f′(x)<0,
故f(x)在(-1,3)上为减函数;
当x∈(3,+∞)时,f′(x)>0,故f(x)在(3,+∞)上为增函数.
由此可见,函数f(x)的单调递增区间为(-∞,-1)和(3,+∞),单调递减区间为(-1,3).
|
题组二 |
导数与函数的极值和最值 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com