
2、在雅典民主政治的“黄金时代”,一个雅典公民不会碰到的事情是
A.他可能被选举为执政官 B.他可能被流放国外10年
C.他可以和妻子一道去参加公民大会 D.他可以对公职人员进行监督
1、《辞海》中“陶片放逐法”的解释:“(雅典)每年初召开民众大会,公民将其认为可能危害民主政治的人的名字记于陶片上;某人票逾半数(通常认为是六千票),则被放逐国外十年。”下列对这一法规理解正确的是
A.体现了奴隶制法律的严酷性 B.表明了雅典物质文化水平较低
C.是雅典维护民主政治的手段 D.反映了雅典民主政治的充分成熟
3.能否正确选用机械能守恒定律解决问题是本节学习的另一难点。通过本节学习应让学生认识到,从功和能的角度分析、解决问题是物理学的重要方法之一;同时进一步明确,在对问题作具体分析的条件下,要能够正确选用适当的物理规律分析、处理问题。
Ⅲ 应用机械能守恒定律解题的步骤:
①选取研究对象----物体系或物体。
②根据研究对象所经历的物理过程,进行受力,做功分析,判断机械能是否守恒。
③恰当地选取参考平面,确定研究对象在过程的初、末态时的机械能。
④根据机械能守恒定律列方程,进行求解。
Ⅳ 只有重力对物体做功时物体的机械能守恒
问题:质量为m的物体自由下落过程中,经过高度h1处速度为v1,下落至高度h2处速度为v2,不计空气阻力,分析由h1下落到h2过程中机械能的变化。
Ⅴ 弹簧和物体组成的系统的机械能
问题:如图,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中
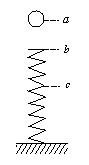
图1-17-3
A.小球和弹簧总机械能守恒
B.小球的重力势能随时间均匀减少
C.小球在b点时动能最大
D.到c点时小球重力势能的减少量等于弹簧弹性势能的增加量
(AD)
Ⅵ 机械能守恒定律的综合应用
[例1]在距离地面20m高处以15m/s的初速度水平抛出一小球,不计空气阻力,取g=10m/s2,求小球落地速度大小。
[例2]小球沿光滑的斜轨道由静止开始滑下,并进入在竖直平面内的离心轨道运动,如图所示,为保持小球能够通过离心轨道最高点而不落下来,求小球至少应从多高处开始滑下?已知离心圆轨道半径为R,不计各处摩擦。
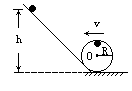
[例3]长l=80cm的细绳上端固定,下端系一个质量 m=100g的小球。将小球拉起至细绳与竖直方向成60°角的位置,然后无初速释放。不计各处阻力,求小球通过最低点时,细绳对小球拉力多大?取g=10m/s2。
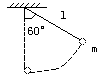
2.分析物体系统所具有的机械能,尤其是分析、判断物体所具有的重力势能,是本节学习的难点之一。在教学中应让学生认识到,物体重力势能大小与所选取的参考平面(零势面)有关;而重力势能的变化量是与所选取的参考平面无关的。在讨论物体系统的机械能时,应先确定参考平面。
1.机械能守恒定律是本章教学的重点内容,本节教学的重点是使学生掌握物体系统机械能守恒的条件;能够正确分析物体系统所具有的机械能;能够应用机械能守恒定律解决有关问题。
3.学习从功和能的角度分析、处理问题的方法,提高运用所学知识综合分析、解决问题的能力。
Ⅱ 重点难点:
2.会用机械能守恒定律解决力学问题,知道应用这个定律的解题步骤,知道用这个定律处理问题的优点.
1.掌握机械能守恒定律,知道它的含义和适用条件,并能判断物体机械能守恒的条件。.
7.72 机械能守恒定律的应用
(第二课时)
Ⅰ 学习目标
10. (2006浙江)已知函数f(x)=x + x
+ x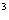 ,数列|x
,数列|x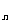 |(x
|(x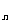 >0)的第一项x
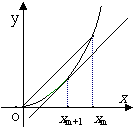
>0)的第一项x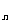 =1,以后各项按如下方式取定:曲线x=f(x)在
=1,以后各项按如下方式取定:曲线x=f(x)在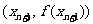 处的切线与经过(0,0)和(x
处的切线与经过(0,0)和(x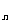 ,f (x
,f (x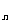 ))两点的直线平行(如图).
))两点的直线平行(如图).
求证:当n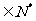 时,
时,
(Ⅰ)x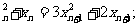
(Ⅱ)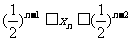

证明:(I)因为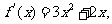
所以曲线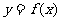 在
在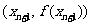 处的切线斜率
处的切线斜率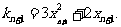
因为过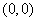 和
和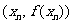 两点的直线斜率是
两点的直线斜率是
所以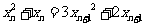 .
.
(II)因为函数 当
当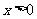 时单调递增,
时单调递增,
而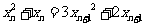
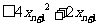
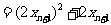 ,
,
所以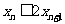 ,即
,即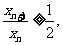
因此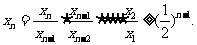
又因为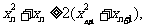 令
令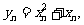 则
则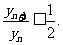
因为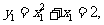 所以
所以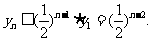
因此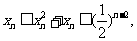 故
故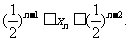
[探索题] 已知函数f(x)=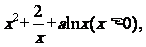 f(x)的导函数是
f(x)的导函数是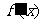
 对任意两个不相等的正数
对任意两个不相等的正数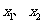 ,证明:当
,证明:当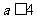 时,
时,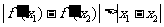

证法一:由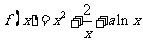 ,得
,得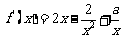
∴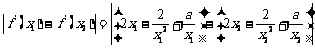
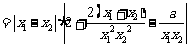
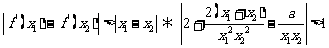
下面证明对任意两个不相等的正数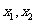 ,有
,有 恒成立
恒成立
即证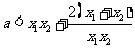 成立
成立
∵
设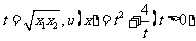 ,则
,则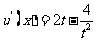
令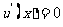 得
得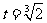 ,列表如下:
,列表如下:
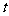 |
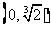 |
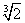 |
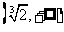 |
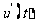 |
 |
 |
 |
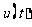 |
 |
极小值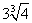 |
 |
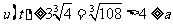 ∴
∴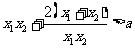
∴对任意两个不相等的正数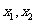 ,恒有
,恒有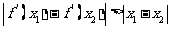
证法二:由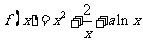 ,得
,得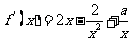
∴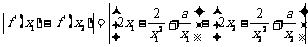
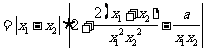
∵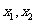 是两个不相等的正数
是两个不相等的正数
∴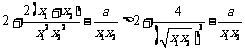

设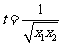 ,
,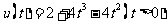
则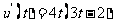 ,列表:
,列表:
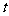 |
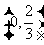 |
 |
 |
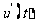 |
 |
 |
 |
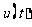 |
 |
极小值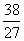 |
 |
∴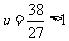 即
即 
∴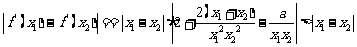
即对任意两个不相等的正数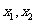 ,恒有
,恒有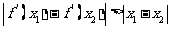
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com