
4.(2006江西)对于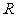 上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有( )
上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有( )
A.f(0)+ f(2)<2 f(1) B. f(0)+ f(2)≤2 f(1)
C. f(0)+ f(2)≥2 f(1) D. f(0)+ f(2)>2 f(1)
3.(2006湖北)若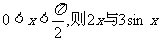 的大小关系 ( )
的大小关系 ( )
A.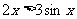 B.
B. C.
C.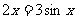 D.与x的取值有关
D.与x的取值有关
2.函数f(x)=sin(3x-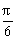 )在点(
)在点(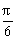 ,
, )处的切线方程是 ( )
)处的切线方程是 ( )
A.3x+2y+ -
- =0, B.3x-2y+
=0, B.3x-2y+ -
- =0
=0
C.3x-2y- -
- =0, D.3x+2y-
=0, D.3x+2y- -
- =0
=0
1.已知a>0,函数f(x)=x3-ax在[1,+∞)上是单调增函数,则a的最大值是
A.0 B.1 C.2 D.3
2.利用导数解不等式问题:(高考中的一类新题型)
(1)利用导数确定函数的单调性,
(2)利用单调性研究不等式。
1.函数的单调性与导数的关系,求单调区间的方法(见上一节);
了解可导函数的单调性与其导数的关系,会用导数分析函数的单调性,进而求解函数不等式的问题;
25、某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元。
(1)求该同学看中的随身听和书包单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
24、已知关于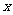 、
、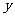 的二元一次方程组
的二元一次方程组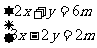 的解满足二元一次方程
的解满足二元一次方程 ,求
,求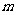 的值。
的值。
23、在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位同学汇报高峰时段的车流量情况如下:
甲同学说:“二环路车流量为每小时10000辆”;
乙同学说:“四环路比三环路车流量每小时多2000辆”;
丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍”;
请你根据他们所提供的信息,求出高峰时段三环路、四环路的车流量各是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com