
4.(2005浙江4).在复平面内,复数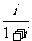 +(1+
+(1+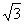 i)2对应的点位于 ( )
i)2对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
[填空题]
3.(2006福建1)设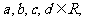 则复数
则复数 为实数的充要条件是( )
为实数的充要条件是( )
A.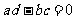 B.
B.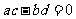 C.
C.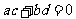 D.
D.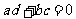
2.(2005广东)若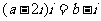 ,其中a、b∈R,i是虚数单位,则
,其中a、b∈R,i是虚数单位,则 =
=
A.0 B.2 C.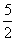 D.5
( )
D.5
( )
1.(2005山东)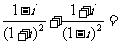 ( )
( )
A.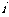 B.
B.  C.
C.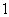 D.
D. 
4.复数问题实数化是解决复数问题的最基本也是最重要的思想方法.
同步练习 5.5复数
[选择题]
3.在复数的求解过程中,要注意复数整体思想的把握和应用;
2.求解计算时,要充分利用i的性质计算问题;
1.复数的加、减、乘、除运算一般用代数形式进行;
[例1]设复数z=lg(m2-2m-2)+(m2+3m+2)i,试求实数m取何值时,(1)z是纯虚数;(2)z是实数;(3)z对应的点位于复平面的第二象限
解:(1)由lg(m2-2m-2)=0,m2+3m+2≠0,得m=3
(2)由m2+3m+2=0,得m=-1或m=-2
(3)由 lg(m2-2m-2)<0,m2+3m+2>0,
得-1<m<1-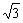 或1+
或1+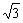 <m<3
<m<3
点评:对复数的分类条件要注意其充要性,对复数相等、共轭复数的概念的运用也是这样
[例2](2005上海)在复数范围内解方程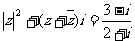 (i为虚数单位)
(i为虚数单位)
解. 原方程化简为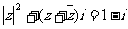 ,
,
设z=x+yi(x、y∈R),代入上述方程得 x2+y2+2xi=1-i,
∴x2+y2=1且2x=-1,解得x=- 且y=±
且y=±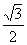 ,
,
∴原方程的解是z=- ±
±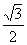 i.
i.
提炼方法:设z=x+yi(x、y∈R),利用复数相等的定义.
[例3]设a∈R,z=x=yi,(x,y∈R),满足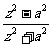 是纯虚数,求x,y应满足的条件
是纯虚数,求x,y应满足的条件
解:设 =ki(k∈R,k≠0)
=ki(k∈R,k≠0)
则z2─a2=ki(z2+a2)Þz2(1─ki)=a2(1+ki),
∴(x2─y2+2xyi)(1─ki)=a2+a2kiÞ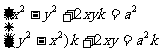 ,
,
消去参数k即得:x2+y2=a2,
◆提炼方法: (1)纯虚数的概念; (2)虚部的概念; (3)化复数问题为实数问题的化归思想(设z=a+bi(a,b∈R));(4)若两个复数能比较大小,则它们都是实数 (5) 实轴,虚轴的概念
[例4](2006春上海) 已知复数 满足
满足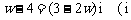 为虚数单位),
为虚数单位),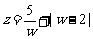 ,求一个以
,求一个以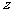 为根的实系数一元二次方程.
为根的实系数一元二次方程.
[解法一] 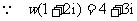 ,∴
,∴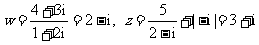 .
.
若实系数一元二次方程有虚根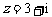 ,则必有共轭虚根
,则必有共轭虚根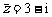 .
.
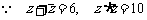 ,
,
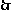 所求的一个一元二次方程可以是
所求的一个一元二次方程可以是 .
.
[解法二] 设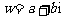
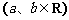
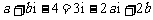 ,
,
得 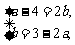
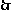
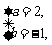
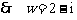 ,
,
以下解法同[解法一].
[研讨.欣赏]设z∈C,求满足z+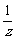 ∈R且|z-2|=2的复数z.
∈R且|z-2|=2的复数z.
分析:设z=a+bi(a、b∈R),代入条件,把复数问题转化为实数问题,易得a、b的两个方程
解法一:设z=a+bi,
则z+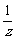 =a+bi+
=a+bi+ =a+bi+
=a+bi+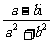
=a+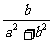 +(b-
+(b-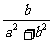 )i∈R
)i∈R
∴b=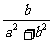 ∴b=0或a2+b2=1
∴b=0或a2+b2=1
当b=0时,z=a,
∴|a-2|=2 ∴a=0或4
a=0不合题意舍去,∴z=4
当b≠0时,a2+b2=1
又∵|z-2|=2,∴(a-2)2+b2=4
解得a=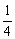 ,b=
,b=
 ,∴z=
,∴z=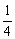 ±
± i
i
综上,z=4或z=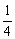 ±
± i
i
解法二:∵z+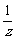 ∈R,
∈R,
∴z+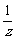 =
=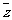 +
+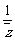
∴(z-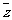 )-
)-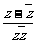 =0,(z-
=0,(z-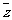 )·
)·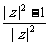 =0
=0
∴z=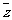 或|z|=1,下同解法一
或|z|=1,下同解法一
点评:解法一设出复数的代数形式,把复数问题转化为实数问题来研究;解法二利用复数是实数的条件复数问题实数化.这些都是解决复数问题的常用方法
8.|z1|>|z2|即(2a-1)x2<1-a2恒成立, 得
得
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com