1、将物体沿竖直方向抛出，物体的运动为竖直上抛运动．抛出后只在重力作用下的运动。

其规律为：(1)v_t=v₀－gt，(2)s=v₀t －½gt²　 (3)v_t²－v₀²=－2gh　

几个特征量：最大高度h= v₀²／2g，运动时间t=2v₀/g．

4、借助等效思想分析运动过程

[例7]图所示为水平导轨，A、B为弹性竖直挡板，相距L＝4 m.小球自A板处开始，以V₀＝4 m/s的速度沿导轨向B运动．它与A、B挡板碰撞后均与碰前大小相等的速率反弹回来，且在导轨上做减速运动的加速度大小不变．为使小球停在AB的中点，这个加速度的大小应为多少？

解析：由于小球与挡板碰后速率不变，运动中加速度大小不变，因此小球在挡板间往复的运动可用一单向的匀减速运动等效替代．要使小球停在A,B中点，它运动的路程应满足

S=nl+l/2,n=0、1、2、…………其中s=v₀²/2a，，……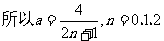

说明：对于分阶段问题，应把握转折点对应的物理量的关系，亦可借助等效思想进行处理．

试题展示

　　　　　　 匀变速直线运动规律的应用

基础知识 一、自由落体运动

　　 物体只受重力作用所做的初速度为零的运动．

特点：(l)只受重力；(2)初速度为零．

规律：(1)v_t=gt；(2)s=½gt²；(3)v_t²=2gs；(4)s=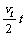；(5)；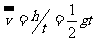

3、分段求解复杂运动

[例5]有一长度为S，被分成几个相等部分在每一部分的末端，质点的加速度增加a/n，若质点以加速度为a，由这一长度的始端从静止出发，求它通过这段距离后的速度多大？

[解析]设每一分段末端的速度分别为v_l、v₂、v₃、……v_n；每一分段的加速度分别为a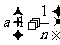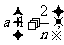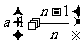；；……。每一等分段的位移为S/n。

根据v_t²－v₀²=2as得v₁²－0=2as/n………①　　　 v₂²－v₁²=2a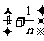s/n………②

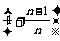v₃²－v₂²=2as/n………③　　　　　　 v_n²－v_n-1²=2as/n

把以上各式相加得v_n²=2a，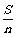

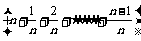
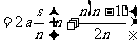
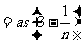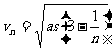
[例6]小球从离地面h=5米高处自由下落，小球每次与地面碰撞后又反弹起来的上升高度总是前一次下落高度的4/5,忽略空气阻力的影响,试求小球从自由下落开始直到最后停在地面上,该整个过程的运动时间。 　(忽略地面与小球碰撞所用的时间，g取10米/秒2)

分析:小球每次下落都是自由落体运动,小球每次反弹上升都是竖直上抛运动,由于不计空气阻力,因此小球上抛到最高点所用的时间与由最高点回落到地面的时间是相等的.

解:小球第一次自由下落时间为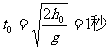，小球从地面第一次碰撞反弹上升及回落的总时间为：

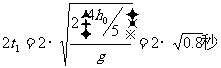，小球从地面第二次碰撞反弹上升及回落的总时间为：

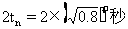
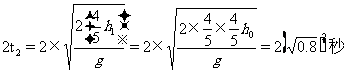
小球从地面第n次碰撞反弹上升及回落的总时间为：

小球从h0处自由下落,直到最后停在地面上,在空中运动的总时间为

答:小球从自由下落开始,直到最后停在地上,在空中运动的总时间为18秒.

说明:在一些力学题中常会遇到等差数列或等比数列等数学问题,每位同学应能熟练地使用这些数学知识解决具体的物理问题.

2、适当使用推理、结论

[例3]两木块自左向右运动，现用高速摄影机在同一底片上多次曝光，记录下木块每次曝光时的位置，如图所示，连续两次曝光的时间间隔是相等的，由图可知

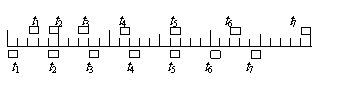A.在时刻t₂以及时刻t₅两木块速度相同

B.在时刻t₁两木块速度相同

C.在时刻t₃和时刻t₄之间某瞬间两木块速度相同

D.在时刻t₄和时刻t₅之间某瞬时两木块速度相同

解：首先由图看出：上边那个物体相邻相等时间内的位移之差为恒量，可以判定其做匀变速直线运动；下边那个物体明显地是做匀速运动。由于t₂及t₅时刻两物体位置相同，说明这段时间内它们的位移相等，因此其中间时刻的即时速度相等，这个中间时刻显然在t₃、t₄之间，因此本题选C。

[例4]一位观察者站在一列火车的第一节车厢的前端旁的站台上进行观察,火车从静止开始作匀加速直线运动,第一节车厢全部通过需时8秒,试问: 　　 (1)16秒内共有几节车厢通过？ 　　 (2)第2节车厢通过需要多少时间？

分析：设每节车厢的长度为s,那么每节车厢通过观察者就意味着火车前进了s距离。于是,原题的意思就变成火车在开始运动的8秒内前进了s,求16秒内前进的距离是几个s,以及前进第2个s所需的时间。此外本题只有两个已知数据，即v₀=0，t=8秒；另一个隐含的条件是车厢长度，解题中要注意消去s。

解: (1)相等时间间隔问题,T=8秒,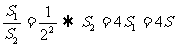

(2)相等位移问题,d=s，

5、解题的基本思路：审题一画出草图一判断运动性质一选取正方向(或建在坐标轴)一选用公式列方程一求解方程，必要时时结果进行讨论

[例2]一初速度为6m/s做直线运动的质点，受到力F的作用产生一个与初速度方向相反、大小为2m／s²的加速度，当它的位移大小为3m时，所经历的时间可能为(　　 )

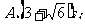
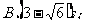
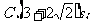
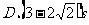
提示：当位移为正时，A．B对；当位移为负时，C对．　　 答案：ABC

4、列运动学方程时，每一个物理量都要对应于同一个运动过程，切忌张冠李戴、乱套公式。

3．本章的题目常可一题多解。解题时要思路开阔，联想比较，筛选最简的解题方案。解题时除采用常规的公式解析法外，图像法、比例法、极值法、逆向转换法(如将一匀减速直线运动视为反向的匀加速直线运动等)等也是本章解题的常用的方法．

2．要分析研究对象的运动过程，搞清整个运动过程按运动性质的特点可分为哪几个运动阶段，各个阶段遵循什么规律，各个阶段间存在什么联系。

1．要养成根据题意画出物体运动示意图的习惯。特别对较复杂的运动，画出草图可使运动过程直观，物理图景清晰，便于分析研究。

4、　 推论：

(l)匀变速直线运动的物体，在任两个连续相等的时间里的位移之差是个恒量，即ΔS＝ S_Ⅱ－ S_Ⅰ＝aT²=恒量．

(2)匀变速直线运动的物体，在某段时间内的平均速度，等于该段时间的中间时刻的瞬时速度，即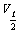==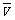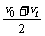．以上两推论在“测定匀变速直线运动的加速度”等学生实验中经常用到，要熟练掌握．

(3)初速度为零的匀加速直线运动(设T为等分时间间隔)：

①　　 IT末、2T末、3T末……瞬时速度的比为V_l∶V₂∶V₃……∶V_n＝1∶2∶3∶……∶n；

②　　 1T内、2T内、3T内……位移的比为S_l∶S₂∶S₃∶……S_n=1²∶2²∶3²∶……∶n²；

③　　 第一个T内，第二个T内，第三个T内……位移的比为S_I∶S_Ⅱ∶S_Ⅲ∶……∶S_N=l∶3∶5∶……∶(2n－1)；

④从静止开始通过连续相等的位移所用时间的比t₁∶t₂∶t₃∶……t_n＝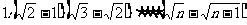

规律方法　　 1、基本规律的理解与应用

[例1]一物体做匀加速直线运动，经A、B、C三点，已知AB＝BC，AB段平均速度为20 m／s，BC段平均速度为30m/s，则可求得(　　 )

　　 A．速度V　　 B．末速度Vc　　 C．这段时间内的平均速度　 D．物体运动的加速度

解析：设s_AB＝s_BC＝s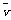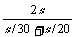，＝m/s=24m/s．

，,

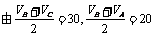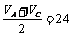得：V_A＝14 m/s，V_B=26m/s，V_C=34m/s　 答案：ABC

解题指导：