3．匀减速直线运动追匀速运动，当二者速度相同时相距最近，此时假设追不上，以后就永远追不上了．

2．匀速运动追击匀加速运动，当二者速度相同时追不上以后就永远追不上了．此时二者相距最近．

1．匀加速运动追击匀速运动，当二者速度相同时相距最远．

2、速度--时间图象的迁移与妙用

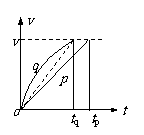
[例4] 一个固定在水平面上的光滑物块，其左侧面是斜面AB，右侧面是曲面AC。已知AB和AC的长度相同。两个小球p、q同时从A点分别沿AB和AC由静止开始下滑，比较它们到达水平面所用的时间

　 A.p小球先到　　 B.q小球先到　　 C.两小球同时到　　 D.无法确定

解：可以利用v-t图象(这里的v是速率，曲线下的面积表示路程s)定性地进行比较。在同一个v-t图象中做出p、q的速率图线，显然开始时q的加速度较大，斜率较大；由于机械能守恒，末速率相同，即曲线末端在同一水平图线上。为使路程相同(曲线和横轴所围的面积相同)，显然q用的时间较少。

[例5] 两支完全相同的光滑直角弯管(如图所示)现有两只相同小球a和a^/ 同时从管口由静止滑下，问谁先从下端的出口掉出？(假设通过拐角处时无机械能损失)　　　

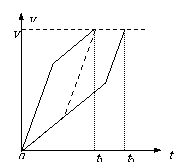解：首先由机械能守恒可以确定拐角处v₁> v₂，而两小球到达出口时的速率v相等。又由题薏可知两球经历的总路程s相等。由牛顿第二定律，小球的加速度大小a=gsinα，小球a第一阶段的加速度跟小球a^/第二阶段的加速度大小相同(设为a₁)；小球a第二阶段的加速度跟小球a^/第一阶段的加速度大小相同(设为a₂)，根据图中管的倾斜程度，显然有a₁> a₂。根据这些物理量大小的分析，在同一个v-t图象中两球速度曲线下所围的面积应该相同，且末状态速度大小也相同(纵坐标相同)。开始时a球曲线的斜率大。由于两球两阶段加速度对应相等，如果同时到达(经历时间为t₁)则必然有s₁>s₂，显然不合理。考虑到两球末速度大小相等(图中v_m)，球a^/ 的速度图象只能如实线所示。因此有t₁< t₂，即a球先到。

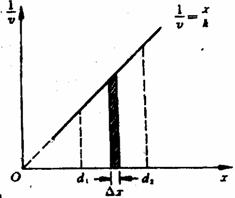[例6]一只老鼠从洞口爬出后沿一直线运动，其速度大小与其离开洞口的距离成反比。当其到达距洞口为d₁的A点时速度为v₁．若B点离洞口的距离为d₂(d₂＞d₁)，求老鼠由A运动至B所需的时间。

[解析]图中的曲线与横轴所围面积的数值正是老鼠经过一定的位移所需的时间。如图所示，取一窄条，其宽度Δx很小(Δx→0)，此段位移所需时间Δt也很小(Δv→0)，可以认为在如此短时间内，老鼠的速度改变很小(Δv→0)，如图中窄条的面积为A＝Δx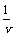=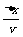，这正表示老鼠经位移Δx所需的时间。故图中，图线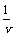=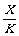，x₁＝d_l，x₂＝d₂及x轴所围的梯形面积正是老鼠由d_l爬至d₂所需的时间。K=v₁d₁=v₂d₂;T=。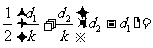

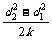
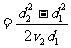说明：利用图象的物理意义来解决实际问题往往起到意想不到的效果．在中学阶段某些问题根本无法借助初等数学的方法来解决，但如果注意到一些图线的斜率和面积所包含的物理意义，则可利用比较直观的方法解决问题。

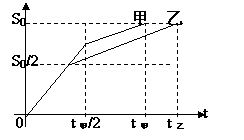
[例7]甲、乙两车同时同向沿直线驶向某地，甲在前一半时间以v₁匀速运动，后一半时间以v₂匀速运动.乙在前一半路程以v₁匀速运动，后一半路程以v₂匀速运动，先到目的地的是____.

[例8]质点P以O点为平衡位置竖直向上作简谐运动，同时质点Q也从O点被竖直上抛，它们恰好同时到达最高点，且高度相同，在此过程中，两质点的瞬时速度v_P与v_Q的关系应该是 [　D　 ]

　A.v_P＞v_Q.　B.先v_P＞v_Q，后v_P＜v_Q，最后v_P=v_Q=0.

　C.v_P＜v_Q.　D.先v_P＜v_Q，后v_P＞v_Q，最后v_P=v_Q=0.

解析：这也是用解析方法很难下手的题目，但若能利用题设条件，画好、分析好两个质点的v－t图线，就能很快找到答案.

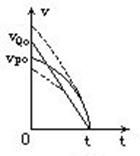　先在图中画出Q作匀减速运动的v－t图象.由于P作简谐运动，当它由平衡位置向极端位置运动过程中，受到的回复力从零开始不断变大，它的加速度也从零开始不断变大，速度不断变小，P作加速度不断增大的减速运动，其v－t图线是一条曲线.根据v－t图线上任一点的切线的斜率数值上等于质点在该时刻的加速度，由于P的加速度由零开始不断变大，画出曲线切线斜率的绝对值也应由零开始不断增大，即曲线的切线应从呈水平状态开始不断变陡，那么只有向右边凸出的下降的曲线才能满足这样的条件.又因P与Q的运动时间相等，所以曲线的终点也应在t，P与Q的路程相等，所以曲线包围的面积应等于三角形v_Q0Ot的面积，根据这些要求，曲线的起点，即质点P的初速度v_P0必定小于Q的初速v_Q0，且两条v－t图线必定会相交，如图7中的实线所示.图7的两条虚线表示的质点P的v－t图线都不满足题设条件(P与Q的路程相等)，所以(D)选项正确.

试题展示

运动学典型问题及解决方法

基础知识　　 一、相遇、追及与避碰问题

对于追及问题的处理，要通过两质点的速度比较进行分析，找到隐含条件(即速度相同时，而质点距离最大或最小)。再结合两个运动的时间关系、位移关系建立相应的方程求解，必要时可借助两质点的速度图象进行分析。　　

2、速度时间图象

(1)它反映了运动物体速度随时间的变化关系．

(2)匀速运动的V一t图线平行于时间轴．

(3)匀变速直线运动的V-t图线是倾斜的直线，其斜率数值上等于物体运动的加速度．

(4)非匀变速直线运动的V一t图线是曲线，每点的切线方向的斜率表示该点的加速度大小．　　

规律方法　 1、s--t图象和v--t图象的应用

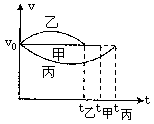
[例1]甲、乙、两三物体同时同地开始做直线运动，其位移一时间图象如图所示，则在t₀时间内，甲、乙、丙运动的平均速度的大小关系分别是：V_甲　　 V_乙　　 V_丙(填“＞”、“＝”或“＜”)，它们在t₀时间内平均速率大小关系为V^/_甲＿V^/_乙＿V^/_丙·

解析：由图可知，在t₀时间内它们的位移相同，由平均速度的定义，故可知甲、乙、两三者在t₀时间内的平均速度的大小相同，即V_甲=V_乙=V_丙，而平均速率是指质点运动的路程(质点运动轨迹的长度)与时间的比值，由图中可知，质点在to时间内，甲的路程最长，(由图象中可知甲有回复运动)故甲的平均速率最大，而乙和丙路程相同，故乙和丙的平均速率相同，即V^/_甲＞V^/_乙=V^/_丙．

注意：平均速率不是平均速度的大小．对于图象问题，要求把运动物体的实际运动规律与图象表示的物理含义结合起来考虑．

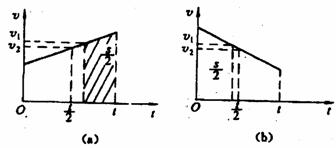[例2]物体沿一直线运动，在t时间内通过的路程为S。它在中间位置½S处的速度为v₁，在中间时刻½t时的速度为v₂，则v₁、v₂的关系为

A．当物体作匀加速直线运动时，v₁＞v₂

B．当物体作匀减速直线运动时，v₁＜v₂；

c．当物体作匀速直线运动时，v₁＝v₂

D．当物体作匀减速直线运动时，v₁＞v₂　　

[解析]由题意，作出物体的v一t关系图，½S点处的虚线把梯形面积一分为二，如图所示，由图可知，无论物体作匀加速直线运动还是作匀减速直线运动。在路程中间位置的速度v₁始终大于中间时刻的速度v₂，当物体作匀速直线运动时，在任何位置和任何时刻的速度都相等。

　　 故正确答案A、C、D。

[例3]甲、乙、丙三辆汽车以相同的速度同时经过某一路标，从此时开始，甲车一直做匀速直线运动，乙车先加速后减速，丙车先减速后加速，它们经过下一路标时速度又相同，则哪一辆车先经过下一个路标？

解析：由题可知这三辆汽车的初、末速度相同，它们发生的位移相同，而题中并不知乙、丙两车在各阶段是否做匀速直线运动，因此，我们只能分析它们的一般运动，即变速直线运动，这样匀变速直线运动的规律就无法求解这一问题，如果我们利用图象法，即在同一坐标系中，分别做出这三辆车的v-t图象，如图所示，由此可知：乙车到达下一个路标的时间最短，即乙车最先通过下一个路标。

说明：图象法是根据物体的运动规律及题中条件，将复杂的运动过程转化成简单、直观过程的一种思维方法。

(1)s--t图象和v--t图象，只能描述直线运动--单向或双向直线运动的位移和速度随时间的变化关系，而不能直接用来描述方向变化的曲线运动。

(2)当为曲线运动时，应先将其分解为直线运动，然后才能用S-t或v一t图象进行描述。

1、位移时间图象

　 位移时间图象反映了运动物体的位移随时间变化的关系，匀速运动的S-t图象是直线，直线的斜率数值上等于运动物体的速度；变速运动的S－t图象是曲线，图线切线方向的斜率表示该点速度的大小．

3、两种运动的联系与应用

[例6]自高为H的塔顶自由落下A物的同时B物自塔底以初速度v₀竖直上抛，且A、B两物体在同一直线上运动．下面说法正确的是(　　 )

　　 A．若v₀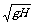＞两物体相遇时，B正在上升途中　　 B、v₀=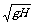两物体在地面相遇

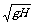　　 C．若＜v₀＜，两物体相遇时B物正在空中下落

　　 D．若v₀＝，则两物体在地面相遇

　 解析：由A、B相对运动知，相遇时间t=H/ v₀，B物上升到最高点需时间t₁= v₀/g．落回到抛出点时间t₂＝2v₀/g

　　 要在上升途中相遇，t＜t₁，即H/ v₀＜v₀/g。v₀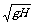＞，要在下降途中相遇．t₁＜ t＜ t₂，即v₀/g＜H/ v₀＜2v₀/g．＜v₀＜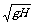

　　 在最高点相遇时t＝t₁，vo=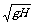；　　 在地面相遇时．t＝t₂，vo=．

答案：ACD

[例7]子弹从枪口射出速度大小是30m/s，某人每隔1s竖直向上开一枪，假设子弹在升降过程中都不相碰，试求

(1)空中最多能有几颗子弹？

(2)设在t=0时将第一颗子弹射出，在哪些时刻它和以后射出的子弹在空中相遇而过？

(3)这些子弹在距原处多高的地方与第一颗子弹相遇？(不计空气阻力，g取10m/s²)

解：(1)设子弹射出后经ts回到原处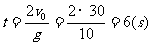

t=0时第一颗子弹射出，它于第6s末回到原处时，第七颗子弹射出，所以空中最多有六颗子弹．

(2)设第一颗子弹在空中运动t₁s，和第二颗子弹在空中相遇．V₁=v₀－gt，V₂=v₀－g(t₁－1)

由对称性v₂=-v₁，即v₀-g(t₁-1)=gt₁-v₀ 解得 t₁=3.5(s)

同理，第一颗子弹在空中运动t₂=4.0s、t₃=4.5s、t₄=5.0s、t₅=5.5s分别与第三颗子弹、第四颗子弹、第五颗子弹、第六颗子弹在空中相遇．

(3)由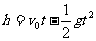，将t₁=3.5s，t₂=4.0s，t₃=4.5s，t₄=5.0s和 t₅=5.5s分别代入上式，得h₁=43.75m，h₂=40m，h₃=33.75m，h₄=25m，h₅=13.75m。

试题展示

　　　　　　 匀变速直线运动图象

基础知识一．对于运动图象要从以下几点来认识它的物理意义：

　　 a．从图象识别物体运动的性质。

　　 b．能认识图像的截距的意义。

　　 C．能认识图像的斜率的意义。

　　 d．能认识图线覆盖面积的意义。

　　 e．能说出图线上一点的状况。

2、充分运用竖直上抛运动的对称性

(1)速度对称：上升和下降过程经过同一位置时速度等大反向。

(2)时间对称：上升和下降过程经过同一段高度的上升时间和下降时间相等。

[例4]某物体被竖直上抛，空气阻力不计，当它经过抛出点之上0.4m时，速度为3m/s．它经过抛出点之下0.4m时，速度应是多少？(g=10m/s²)

解法一：竖直上抛物体的上抛速度与落回原抛出点速度大小相等．因此，物体在抛出点之上0.4m处，上升阶段或下降阶段的速度大小都是3m/s．若以下落速度3m/s为初速度，0.4+0.4(m)为位移量，那么所求速度就是设问的要求．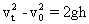

解法二 ：物体高度为h₁=0.4m时速度为v₁，则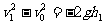

物体高度为h₂=-0.4m时速度为v₂，则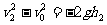

由以上两式式消去v₀得_，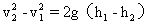

[例5]一个从地面竖直上抛的物体，它两次经过一个较低的点a的时间间隔是Ta，两次经过一个较高点b的时间间隔是Tb，则a、b之间的距离为(　　 )

；　 ；　 ；　　

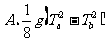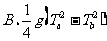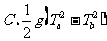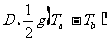
解析：根据时间的对称性，物体从a点到最高点的时间为Ta/2，从b点到最高点的时间为Tb/2，所以a点到最高点的距离ha=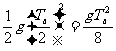，b点到最高点的距离hb=，

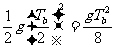故a、b之间的距离为ha－hb=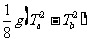，即选A

3．上升阶段与下降阶段的特点

　(l)物体从某点出发上升到最高点的时间与从最高点回落到出发点的时们相等。即　 t_上=v₀/g=t_下　 所以，从某点抛出后又回到同一点所用的时间为t=2v₀/g

　(2)上把时的初速度v₀与落回出发点的速度V等值反向，大小均为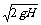；即　　 V=V₀=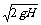

　　 注意：①以上特点适用于竖直上抛物体的运动过程中的任意一个点所时应的上升下降两阶段，因为从任意一点向上看，物体的运动都是竖直上抛运动，且下降阶段为上升阶段的逆过程．

　　 ②以上特点，对于一般的匀减速直线运动都能适用。若能灵活掌握以上特点，可使解题过程大为简化．尤其要注意竖直上抛物体运动的时称性和速度、位移的正负。

规律方法　　　 1、基本规律的理解与应用

[例1]从一定高度的气球上自由落下两个物体，第一物体下落1s后，第二物体开始下落，两物体用长93.1m的绳连接在一起．问：第二个物体下落多长时间绳被拉紧．

解法一　 设第二个物体下落ts后绳被拉紧，此时两物体位移差Δh=93.1m

Δh=，即93.1=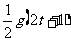，解得　 t=9(s)

解法二　 以第二个物体为参照物．在第二个物体没开始下落时，第一个物体相对第二个物体做自由落体运动；1s后，第二个物体开始下落，第一个物体相对第二个物体做匀速运动，其速度为第一个物体下落1s时的速度．当绳子被拉直时，第一个物体相对第二个物体的位移为h=93.1m．h=h₁+h₂

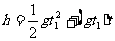，即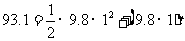　　 解得　　　 t=9(s)

[例2]利用水滴下落可以测量重力加速度g，调节水龙头，让水一滴一滴地流出。在水龙头的正下方放一个盘子，调整盘子的高度，使一个水滴碰到盘子时，恰好有另一个水滴从水龙头开始下落，而空中还有一个正在下落的水滴。测出水龙头到盘子的距离为h，再用秒表测时间。从第一个水滴离开水龙头开时计时，到第n个水滴落到盘子中，共用时间为t₀问：第一个水滴落到盘中时，第二个水滴离开水龙头的距离为多少？可测得的重力加速度为多少？

[解析]由于水龙头滴水的时间间隔是恒定的，因此，题中所提到的某一时刻恰好滴到盘子的水滴和正在空中下落的水滴，这两个水滴的状态可以看做是同一个水滴离开水龙头做自由落体运动的两个状态：滴到盘子的水滴运动时间为2t₁，正在空中下落的水滴的位置相当于下落时间为t₁的位置，通过比例关系可解每个水滴在下落的一半时间内的下落高度即为所求。依题意数清楚在计时t内有多少个水滴离开水龙头，就得到了相邻两滴水滴落下的时间间隔，将此时间间隔用于开始下落的过程上，可解出重力加速度的表达式。

　　 解：滴水的时间间隔恒定，视为同一滴水在下落h段的时间分为相等的两段，前段时间内下落h₁．则由初速为零的匀加速直线运动的比例关系，有:h_l：h＝1：4；而h_l就是第一个水滴落到盘中时，第二个水滴离开水龙头的距离：h₀。从开始计时到第n个水滴落到盘子中，共有(n+1)个水滴离开水龙头，相邻两滴水滴落下的时间间隔为t₁＝。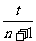

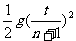从开始下落经历t₁下落了h，由h＝得：g＝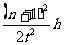

[例3]将一轻质球竖直上抛，若整个运动过程中，该球所受空气阻力大小不变，上升时间为t_上，下降时间为 t_下，抛出时速度为 v₀，落回时速度为v_t，则它们间的关系是(　 )

　　 A．t_上＞t_下，v₀＞v_t； B．t_上＜t_下，v₀＜v_t　　 C．t_上＜t_下，v₀＞v_t；D．t_上=t_下，v₀＝v_t

解析：a_上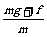＝，a_下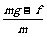＝，所以a_上＞a_下． t_上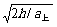＝，t_下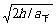＝。所以t_上＜t_下，v₀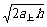＝，v_t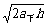＝，所以v₀＞v_t　　 答案：C

2．两种处理办法：

(1)分段法：上升阶段看做末速度为零，加速度大小为g的匀减速直线运动，下降阶段为自由落体运动．

(2)整体法：从整体看来，运动的全过程加速度大小恒定且方向与初速度v₀方向始终相反，因此可以把竖直上抛运动看作是一个统一的减速直线运动。这时取抛出点为坐标原点，初速度v₀方向为正方向，则a=一g。