
20.(16分)设函数f(x)=sin(2x+ )(-
)(- <
< <0),y=f(x)图象的一条对称轴是直线x=
<0),y=f(x)图象的一条对称轴是直线x= .
.
(1)求 ;
;
(2)求函数y=f(x)的单调增区间;
(3)证明:直线5x-2y+c=0与函数y=f(x)的图象不相切.
(1)解 ∵x= 是函数y=f(x)的图象的对称轴,
是函数y=f(x)的图象的对称轴,
∴sin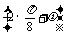 =±1,
=±1,
∴ +
+ =k
=k +
+ ,k∈Z.
,k∈Z.
∵- <
< <0,∴
<0,∴ =-
=- .
.
(2)解 由(1)知 =-
=- ,因此y=sin
,因此y=sin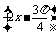 .
.
由题意得2k -
- ≤2x-
≤2x- ≤2k
≤2k +
+ ,k∈Z.
,k∈Z.
则k +
+ ≤x≤k
≤x≤k +
+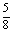
 ,k∈Z
,k∈Z
所以函数y=sin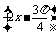 的单调增区间为
的单调增区间为
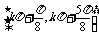 ,k∈Z.
,k∈Z.
(3)证明 ∵|y′|=|(sin(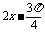 ))′|
))′|
=|2cos(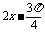 )|≤2,
)|≤2,
∴曲线y=f(x)的切线斜率的取值范围是[-2,2],而直线5x-2y+c=0的斜率为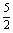 >2,所以直线5x-2y+c=0与函数
>2,所以直线5x-2y+c=0与函数
y=sin(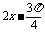 )的图象不相切.
)的图象不相切.
19.(16分)把曲线C:y=sin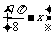 ·cos
·cos 向右平移a (a>0)个单位,得到的曲线C′关于直线x=
向右平移a (a>0)个单位,得到的曲线C′关于直线x= 对称.
对称.
(1)求a的最小值;
(2)就a的最小值证明:当x∈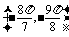 时,曲线C′上的任意两点的直线斜率恒大于零.
时,曲线C′上的任意两点的直线斜率恒大于零.
(1)解 ∵y=sin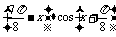
=sin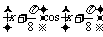
= sin
sin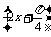 ,
,
∴曲线C′方程为y= sin
sin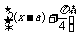 ,
,
它关于直线x= 对称,
对称,
∴ sin
sin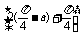 =±
=± ,
,
即2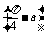 +
+ =k
=k +
+ (k∈Z),
(k∈Z),
解得a= -
-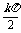 (k∈Z),
(k∈Z),
∵a>0,∴a的最小值是 .
.
(2)证明 当a= 时,曲线C′的方程为y=
时,曲线C′的方程为y= sin2x.
sin2x.
由函数y= sin2x的图象可知:
sin2x的图象可知:
当x∈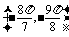 时,函数y=
时,函数y= sin2x是增函数,
sin2x是增函数,
所以当x1<x2时,有y1<y2,
所以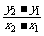 >0,即斜率恒大于零.
>0,即斜率恒大于零.
18.(16分)已知tan 、tan
、tan 是方程x2-4x-2=0的两个实根,求:cos2(
是方程x2-4x-2=0的两个实根,求:cos2( +
+ )+2sin(
)+2sin( +
+ )cos(
)cos( +
+ )-3sin2(
)-3sin2( +
+ )的值.
)的值.
解 由已知有tan +tan
+tan =4,tan
=4,tan ·tan
·tan =-2,
=-2,
∴tan( +
+ )=
)=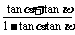 =
=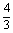 ,
,
cos2( +
+ )+2sin(
)+2sin( +
+ )cos(
)cos( +
+ )-3sin2(
)-3sin2( +
+ )
)
=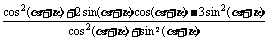
=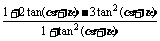
=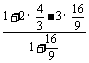 =-
=- .
.
17.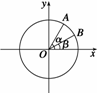 (2008·江苏,15)(14分)如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角
(2008·江苏,15)(14分)如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角 ,
,
 ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为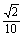 ,
,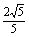 .
.
(1)求tan( +
+ )的值;
)的值;
(2)求 +2
+2 的值.
的值.
解 由条件得cos =
=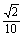 ,cos
,cos =
=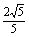 .
.
∵ ,
, 为锐角,
为锐角,
∴sin =
= =
=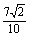 ,
,
sin =
=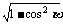 =
=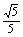 .
.
因此tan =
=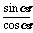 =7,tan
=7,tan =
=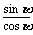 =
= .
.
(1)tan( +
+ )=
)=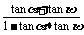 =
=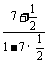 =-3.
=-3.
(2)∵tan2 =
=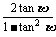 =
=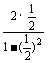 =
=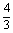 ,
,
∴tan( +2
+2 )=
)=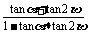 =
=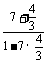 =-1.
=-1.
∵ ,
, 为锐角,∴0<
为锐角,∴0< +2
+2 <
<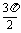 ,∴
,∴ +2
+2 =
= .
.
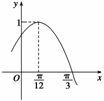
16.(14分)已知函数f(x)=Asin(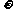 x+
x+ )(A>0,
)(A>0, 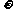 >0,|
>0,| |<
|< ) (x∈R)的部分图象如图所示.
) (x∈R)的部分图象如图所示.
(1)求f(x)的表达式;
(2)设g(x)=f(x)- f
f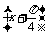 ,求函数g(x)的最小值及相应的x的取值集合.
,求函数g(x)的最小值及相应的x的取值集合.
解 (1)由图象可知:A=1,
函数f(x)的周期T满足: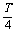 =
=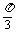 -
-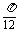 =
= ,T=
,T= ,
,
∴T=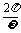 =
= .∴
.∴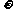 =2.∴f(x)=sin(2x+
=2.∴f(x)=sin(2x+ ).
).
又f(x)图象过点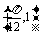 ,
,
∴f =sin
=sin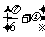 =1,
=1,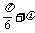 =2kπ+
=2kπ+ (k∈Z).
(k∈Z).
又| |<
|< ,故
,故 =
=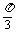 .∴f(x)=sin
.∴f(x)=sin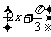 .
.
(2)方法一 g(x)=f(x)- f
f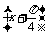
=sin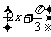 -
- sin
sin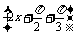
=sin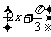 -
- sin
sin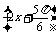
= sin2x+
sin2x+ cos2x+
cos2x+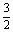 sin2x-
sin2x- cos2x
cos2x
=2sin2x,
由2x=2k -
- (k∈Z),得x=k
(k∈Z),得x=k -
- (k∈Z),
(k∈Z),
|
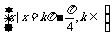 .
.
方法二 g(x)=f(x)- f
f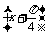
=sin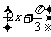 -
- sin
sin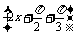
=sin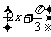 -
- cos
cos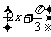
=2sin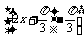 =2sin2x,
=2sin2x,
由2x=2k -
- (k∈Z),得x=k
(k∈Z),得x=k -
- (k∈Z),
(k∈Z),
∴g(x)的最小值为-2,相应的x的取值集合为{x|x=k -
- ,k∈Z}.
,k∈Z}.
15.(14分)已知 ∈
∈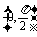 ,
, ∈
∈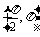 且sin(
且sin( +
+ )=
)=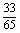 ,cos
,cos =-
=-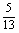 .求sin
.求sin .
.
解 ∵ ∈
∈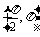 ,cos
,cos =-
=-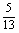 ,∴sin
,∴sin =
=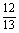 .
.
又∵0< <
< ,
, <
< <
< ,∴
,∴ <
< +
+ <
<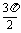 ,
,
又sin( +
+ )=
)=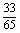 ,
,
∴ <
< +
+ <
< ,cos(
,cos( +
+ )=-
)=-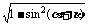
=-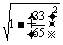 =-
=- ,
,
∴sin =sin[(
=sin[( +
+ )-
)- ]
]
=sin( +
+ )cos
)cos -cos(
-cos( +
+ )sin
)sin
 =
=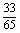 ·
·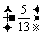 -
-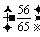 ·
·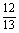 =
= .
.
14.关于函数f(x)=2sin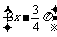 ,有下列命题:
,有下列命题:
①其最小正周期为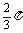 ;
;
②其图象由y=2sin3x向左平移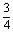 个单位而得到;
个单位而得到;
③在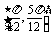 上为单调递增函数,则其中真命题为
(写出你认为正确答案的序号).
上为单调递增函数,则其中真命题为
(写出你认为正确答案的序号).
答案 ①③
13.若f(x)=asin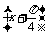 +bsin
+bsin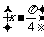 (ab≠0)是偶函数,则有序实数对(a,b)可以是
.(注:只要填满足a+b=0的一组数字即可)
(ab≠0)是偶函数,则有序实数对(a,b)可以是
.(注:只要填满足a+b=0的一组数字即可)
答案 (1,-1)
12.函数f(x)=sinx+2|sinx|,x∈[0,2 ]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是 .
]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是 .
答案 1<k<3
11.若cos( +
+ )=
)=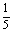 ,cos(
,cos( -
- )=
)= ,则tan
,则tan ·tan
·tan =
.
=
.
答案 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com